Aufgaben:Exercise 5.3: Mean Square Error

• Return to book

Gaußimpuls, Rechteckimpuls, Spaltimpuls und einige Kenngrößen

We consider three pulse-like signals, namely

• a  Gaussian pulse  with amplitude  $A$  and equivalent duration  $T$:

$$x_1(t) = A \cdot {\rm e}^{- \pi (t/T)^2} \hspace{0.05cm},$$

• a  Rectangular pulse  $x_2(t)$  with amplitude  $A$  and (equivalent) duration  $T$:

$$x_2(t) = \left\{ \begin{array}{c} A \\ 0 \\ \end{array} \right.\quad \begin{array}{*{10}c} {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{20}c} |t| < T/2 \hspace{0.05cm}, \\ |t| > T/2 \hspace{0.05cm}, \\ \end{array}$$

• a so called  Sinc pulse  according to the following definition:

$$x_3(t) = A \cdot {\rm si}(\pi \cdot t/ T) ,\hspace{0.15cm}{\rm si}(x) = \sin(x)/x\hspace{0.05cm}.$$

Let the signal parameters be  $A = 1\ {\rm V}$  and  $T = 1\ {\rm ms}$ in each case.

The conventional  Fourier Transform  leads to the following spectral functions:

• $X_1(f)$  is also Gaussian,
• $X_2(f)$  runs according to the  $\rm si$–function,
• $X_3(f)$  is constant for  $|f| < 1/(2 T)$  and outside zero.

For all spectral functions,  $X(f = 0) = A \cdot T$.

If the discrete-frequency spectrum is determined by the  Discrete Fourier Transform(DFT)  (DFT) with the DFT parameters

• $N = 512$   ⇒   number of samples considered in the time and frequency domain,*$f_{\rm A}$   ⇒   interpolation distance in the frequency domain,

this will lead to distortions due to truncation and/or aliasing errors.

DThe other DFT parameters are clearly fixed withn&bsp; $N$  uan  $f_{\rm A}$  .Fhe following applies to these:

$$f_{\rm P} = N \cdot f_{\rm A},\hspace{0.3cm}T_{\rm P} = 1/f_{\rm A},\hspace{0.3cm}T_{\rm A} = T_{\rm P}/N \hspace{0.05cm}.$$

DThe accuracy of the respective DFT approximation is captured by thenbsp; mean square error  (MSE):

$${\rm MQF} = \frac{1}{N}\cdot \sum_{\mu = 0 }^{N-1} \left|X(\mu \cdot f_{\rm A})-\frac{D(\mu)}{f_{\rm A}}\right|^2 \hspace{0.05cm}.$$

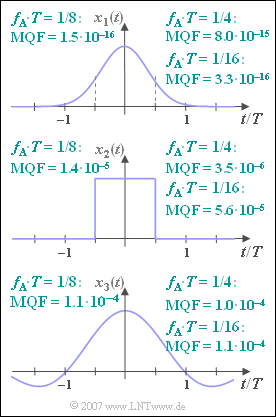
Die sich ergebenden MQF–Werte sind in obiger Grafik angegeben, gültig für  $N = 512$  sowie für

• $f_{\rm A} \cdot T = 1/4$,
• $f_{\rm A} \cdot T = 1/8$,
• $f_{\rm A} \cdot T = 1/16$.

Hinweise:

• Die Aufgabe gehört zum Kapitel  Fehlermöglichkeiten bei Anwendung der DFT.

• Die Theorie zu diesem Kapitel ist im Lernvideo  Fehlermöglichkeiten bei Anwendung der DFT  zusammengefasst.

Fragebogen

1

Welcher Bereich  $|f| \leq f_{\text{max}}$  wird mit  $N = 512$  und  $f_{\rm A} \cdot T = 1/8$  erfasst?

$f_{\text{max}} \cdot T\ = \ $

2

In welchem Zeitabstand  $T_{\rm A}$  liegen die Abtastwerte von  $x(t)$  vor?

$T_{\rm A}/T\ = \ $

3

Aufgrund welcher Effekte erhöht sich der MQF–Wert für den Gaußimpuls, wenn man  $f_{\rm A} \cdot T = 1/4$  anstelle von  $f_{\rm A} \cdot T = 1/8$  verwendet?

	Der Abbruchfehler wird signifikant vergrößert.
	Der Aliasingfehler wird signifikant vergrößert.

4

Aufgrund welcher Effekte erhöht sich der MQF–Wert für den Gaußimpuls, wenn man  $f_{\rm A} \cdot T = 1/16$  anstelle von $f_{\rm A} \cdot T = 1/4$  verwendet?

	Der Abbruchfehler wird signifikant vergrößert.
	Der Aliasingfehler wird signifikant vergrößert.

5

Vergleichen Sie die MQF–Werte des Rechteckimpulses  $x_2(t)$  mit denen des Gaußimpulses  $x_1(t)$. Welche der folgenden Aussagen treffen zu?

	$\rm MQF$  wird größer, da die Spektralfunktion  $X_2(f)$  asymptotisch langsamer abfällt als  $X_1(f)$.
	Es dominiert der Aliasingfehler.
	Es dominiert der Abbruchfehler.

6

Vergleichen Sie die MQF–Werte des Spaltimpulses  $x_3(t)$  mit denen des Gaußimpulses  $x_1(t)$. Welche der folgenden Aussagen treffen zu?

	$\rm MQF$  wird größer, da die Spektralfunktion  $X_3(f)$  asymptotisch langsamer abfällt als  $X_1(f)$.
	Es dominiert der Aliasingfehler.
	Es dominiert der Abbruchfehler.

Musterlösung

Solution

(1)  Mit den DFT–Parametern  $N = 512$  und  $f_{\rm A} \cdot T = 1/8$  folgt nach Multiplikation der beiden Größen:

$$f_{\rm P} \cdot T = N \cdot (f_{\rm A} \cdot T) = 64.$$

• Dadurch wird der Frequenzbereich  $–f_{\rm P}/2 \leq f < f_{\rm P}/2$  erfasst:

$$f_{\rm max }\cdot T \hspace{0.15 cm}\underline{= 32}\hspace{0.05cm}.$$

(2)  Die Periodifizierung der Zeitfunktion basiert auf dem Parameter  $T_{\rm P} = 1/f_{\rm A} = 8T$.

• Der Abstand zweier Abtastwerte beträgt somit

$$T_{\rm A}/T = \frac{T_{\rm P}/T}{N} = \frac{8}{512}\hspace{0.15 cm}\underline{ = 0.015625}\hspace{0.05cm}.$$

(3)  Richtig ist der Lösungsvorschlag 1   ⇒   Erhöhung des Abbruchfehlers:

• Mit dieser Maßnahme wird gleichzeitig  $T_{\rm P}$  von  $8T$  auf  $4T$  halbiert.
• Berücksichtigt werden somit nur noch Abtastwerte im Bereich  $–2T \leq t < 2T$, wodurch der Abbruchfehler erhöht wird.
• Der mittlere quadratische Fehler  $(\rm MQF)$  steigt dadurch beim Gaußimpuls  $x_1(t)$  von  $0.15 \cdot 10^{-15}$  auf  $8 \cdot 10^{-15}$, obwohl der Aliasingfehler durch diese Maßnahme sogar etwas kleiner wird.

(4)  Richtig ist der Lösungsvorschlag 2   ⇒   Erhöhung des Aliasingfehlers:

• Durch die Halbierung von  $f_{\rm A}$  wird auch  $f_{\rm P}$  halbiert.
• Dadurch wird der Aliasingfehler etwas größer bei gleichzeitig kleinerem Abbruchfehler.
• Insgesamt steigt beim Gaußimpuls  $x_1(t)$  der mittlere quadratische Fehler  $(\rm MQF)$  von  $1.5 \cdot 10^{-16}$  auf  $3.3 \cdot 10^{-16}$.

(5)  Richtig sind die Lösungsvorschläge 1 und 2:

• Wie aus der Grafik zu ersehen ist, trifft die letzte Aussage nicht zu im Gegensatz zu den ersten beiden.
• Aufgrund des langsamen,  $\rm si$–förmigen Abfalls der Spektralfunktion dominiert der Aliasingfehler.
• Der  $\rm MQF$–Wert ist bei  $f_{\rm A} \cdot T = 1/8$  mit  $1.4 \cdot 10^{-5}$  deshalb deutlich größer als beim Gaußimpuls  $(1.5 \cdot 10^{-16})$.

(6)  Richtig ist der Lösungsvorschlag 3:

• Die Spektralfunktion  $X_3(f)$  hat hier einen rechteckförmigen Vorlauf, so dass die beiden ersten Aussagen nicht zutreffen.
• Dagegen ist bei dieser  $\rm si$–förmigen Zeitfunktion ein Abbruchfehler unvermeidbar. Dieser führt zu den angegebenen großen  $\rm MQF$–Werten.