Difference between revisions of "Aufgaben:Exercise 2.2Z: Real Two-Path Channel"
From LNTwww
m (Text replacement - "Category:Exercises for Mobile Communications" to "Category:Mobile Communications: Exercises") |
|||
| (15 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Mobile_Communications/Multipath_Reception_in_Mobile_Communications}} |
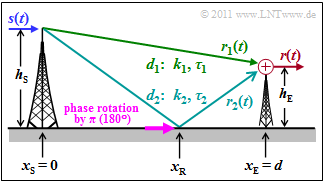
| − | [[File: | + | [[File:EN_Mob_A_2_2Z.png|right|frame|Two-path scenario]] |
The sketched scenario is considered in which the transmitted signal $s(t)$ reaches the antenna of the receiver via two paths: | The sketched scenario is considered in which the transmitted signal $s(t)$ reaches the antenna of the receiver via two paths: | ||
| − | $$r(t) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} r_1(t) + r_2(t) =k_1 \cdot s( t - \ | + | :$$r(t) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} r_1(t) + r_2(t) =k_1 \cdot s( t - \tau_1) + k_2 \cdot s( t - \tau_2) |
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
Note the following: | Note the following: | ||
| − | * The | + | * The delays $\tau_1$ and $\tau_2$ of the main and the secondary paths can be calculated from the path lengths $d_1$ and $d_2$ using the speed of light $c = 3 \cdot 10^8 \ \rm m/s$ . |
| − | * The amplitude factors $k_1$ and $k_2$ are | + | * The amplitude factors $k_1$ and $k_2$ are obtained according to the path loss model with path loss exponent $\gamma = 2$ (free–space attenuation). |
| − | * The height of the | + | * The height of the transmit antenna is $h_{\rm S} = 500 \ \rm m$. The height of the receiving antenna is $h_{\rm E} = 30 \ \rm m$. The antennas are separated by a distance of $d = 10 \ \ \rm km$. |
| − | * The reflection on the secondary path causes a phase change of $\pi$, so that the partial signals must be subtracted. This is taken into account by a negative $k_2$ | + | * The reflection on the secondary path causes a phase change of $\pi$, so that the partial signals must be subtracted. This is taken into account by a negative $k_2$ value. |
| Line 18: | Line 18: | ||
''Note:'' | ''Note:'' | ||
| − | * This task belongs to the chapter [[ | + | * This task belongs to the chapter [[Mobile_Communications/Multi-Path_Reception_in_Mobile_Communications| Multi–Path Reception in Mobile Communications]]. |
| Line 25: | Line 25: | ||
===Questionnaire=== | ===Questionnaire=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Calculate the length $d_1$ of the direct path | + | {Calculate the length $d_1$ of the direct path. |
|type="{}"} | |type="{}"} | ||
$d_1 \ = \ ${ 10011 1% } $\ \ \rm m$ | $d_1 \ = \ ${ 10011 1% } $\ \ \rm m$ | ||
| − | {Calculate the length $d_2$ of the | + | {Calculate the length $d_2$ of the reflected path. |
|type="{}"} | |type="{}"} | ||
$d_2 \ = \ ${ 10014 1% } $\ \ \rm m$ | $d_2 \ = \ ${ 10014 1% } $\ \ \rm m$ | ||
| Line 36: | Line 36: | ||
|type="{}"} | |type="{}"} | ||
$\Delta d \ = \ ${ 2,996 3% } $\ \ \rm m$ | $\Delta d \ = \ ${ 2,996 3% } $\ \ \rm m$ | ||
| − | $\ Delta \tau \ = \ ${ 9,987 3% } $\ \ \rm ns$ | + | $\Delta \tau \ = \ ${ 9,987 3% } $\ \ \rm ns$ |
| − | {What equation results for the | + | {What equation results for the path delay difference $\Delta \tau$ with the approximation $\sqrt{(1 + \varepsilon)} \approx 1 + \varepsilon/2$ valid for small $\varepsilon$ ? |
|type="[]"} | |type="[]"} | ||
- $\Delta \tau = (h_{\rm S} \ - h_{\rm E})/d$, | - $\Delta \tau = (h_{\rm S} \ - h_{\rm E})/d$, | ||
| Line 46: | Line 46: | ||
{Which statements apply for the amplitude coefficients $k_1$ and $k_2$ ? | {Which statements apply for the amplitude coefficients $k_1$ and $k_2$ ? | ||
|type="[]"} | |type="[]"} | ||
| − | + The coefficients $k_1$ and $k_2$ are almost equal in | + | + The coefficients $k_1$ and $k_2$ are almost equal in magnitude. |
| − | - The | + | - The magnitudes $|k_1|$ and $|k_2|$ differ significantly. |
+ The coefficients $|k_1|$ and $|k_2|$ differ in sign. | + The coefficients $|k_1|$ and $|k_2|$ differ in sign. | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' According to | + | '''(1)''' According to Pythagoras: |
| − | $$d_1 = \sqrt{d^2 + (h_{\rm S}- h_{\rm E})^2} = \sqrt{10^2 + (0.5- 0.03)^2} \,\,{\rm km} \hspace{0.1cm} \underline {=10011.039\,{\rm m}} | + | :$$d_1 = \sqrt{d^2 + (h_{\rm S}- h_{\rm E})^2} = \sqrt{10^2 + (0.5- 0.03)^2} \,\,{\rm km} \hspace{0.1cm} \underline {=10011.039\,{\rm m}} |
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
*Actually, specifying such a length with an accuracy of one millimeter is not very useful and contradicts the mentality of an engineer. | *Actually, specifying such a length with an accuracy of one millimeter is not very useful and contradicts the mentality of an engineer. | ||
| − | *We have done this anyway to be able to check the accuracy of the approximation | + | *We have done this anyway to be able to check the accuracy of the approximation in subtask '''(4)'''. |
| − | '''(2)''' If you fold the reflected beam right | + | '''(2)''' If you fold the reflected beam on the right side of $x_{\rm R}$ downwards (reflection on the ground), you get again a right triangle. From this follows: |
| − | $$d_2 = \sqrt{d^2 + (h_{\rm S}+ h_{\rm E})^2} = \sqrt{10^2 + (0.5+ 0.03)^2} \,\,{\rm km} \hspace{0.1cm} \underline {=10014.035\,{\rm m}} | + | :$$d_2 = \sqrt{d^2 + (h_{\rm S}+ h_{\rm E})^2} = \sqrt{10^2 + (0.5+ 0.03)^2} \,\,{\rm km} \hspace{0.1cm} \underline {=10014.035\,{\rm m}} |
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | '''(3)''' | + | '''(3)''' Using the results from '''(1)''' and '''(2)''', the length and delay differences are: |
| − | :$$\Delta d = d_2 - d_1 = \hspace{0.1cm} \underline {=2 | + | :$$\Delta d = d_2 - d_1 = \hspace{0.1cm} \underline {=2.996\,{\rm m}} |
\hspace{0.05cm},\hspace{1cm} | \hspace{0.05cm},\hspace{1cm} | ||
| − | \ | + | \Delta \tau = \frac{\Delta d}{c} = \frac{2.996\,{\rm m}}{3 \cdot 10^8 \,{\rm m/s}} \hspace{0.1cm} \underline {=9.987\,{\rm ns}} |
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | '''(4)''' With $h_{\rm S} + h_{\rm E} \ll d$ the above equation can be expressed as follows: | + | |
| − | $$d_1 \hspace{-0.1cm} \ = \ \hspace{-0.1cm} d \cdot \sqrt{1 + \frac{(h_{\rm S}- h_{\rm E})^2}{d^2} \approx d \cdot \left [ 1 + \frac{(h_{\rm S}- h_{\rm E})^2}{2d^2} \right ] \hspace{0.05cm},\hspace{1cm} | + | '''(4)''' With $h_{\rm S} + h_{\rm E} \ll d$ the above equation can be expressed as follows: |
| − | d_2 \hspace{-0.1cm} \ = \ \hspace{-0.1cm} d \cdot \sqrt{1 + \frac{(h_{\rm S}+ h_{\rm E})^2}{d^2} \approx d \cdot \left [ 1 + \frac{(h_{\rm S}+ h_{\rm E})^2}{2d^2} \right ] $$ | + | :$$d_1 \hspace{-0.1cm} \ = \ \hspace{-0.1cm} d \cdot \sqrt{1 + \frac{(h_{\rm S}- h_{\rm E})^2}{d^2}} \approx d \cdot \left [ 1 + \frac{(h_{\rm S}- h_{\rm E})^2}{2d^2} \right ] \hspace{0.05cm},\hspace{1cm} |
| − | $$\Rightarrow \hspace{0.3cm} \ | + | d_2 \hspace{-0.1cm} \ = \ \hspace{-0.1cm} d \cdot \sqrt{1 + \frac{(h_{\rm S}+ h_{\rm E})^2}{d^2}} \approx d \cdot \left [ 1 + \frac{(h_{\rm S}+ h_{\rm E})^2}{2d^2} \right ] $$ |
| − | = \frac {2 \cdot h_{\rm S}\cdot h_{\rm E}}{d}\hspace{0.3cm} | + | :$$\Rightarrow \hspace{0.3cm} \Delta d = d_2 - d_1 \approx \frac {1}{2d} \cdot \left [ (h_{\rm S}+ h_{\rm E})^2 - (h_{\rm S}- h_{\rm E})^2 \right ] |
| − | \Rightarrow \hspace{0.3cm} \ | + | = \frac {2 \cdot h_{\rm S}\cdot h_{\rm E}}{d}\hspace{0.3cm} |
| + | \Rightarrow \hspace{0.3cm} \Delta \tau = \frac{\Delta d}{c} \approx \frac {2 \cdot h_{\rm S}\cdot h_{\rm E}}{c \cdot d} | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | *So the correct solution is the <u>solution 3</u>. With the given numerical values | + | *So the correct solution is the <u>solution 3</u>. With the given numerical values, we have |
| − | $$\Delta \tau \approx \frac {2 \cdot 500\,{\rm m}\cdot 30\,{\rm m}}{3 \cdot 10^8 \,{\rm m/s} \cdot 10000\,{\rm m}} = 10^{-8}\,{\rm s} = 10\,{\rm ns} | + | :$$\Delta \tau \approx \frac {2 \cdot 500\,{\rm m}\cdot 30\,{\rm m}}{3 \cdot 10^8 \,{\rm m/s} \cdot 10000\,{\rm m}} = 10^{-8}\,{\rm s} = 10\,{\rm ns} |
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | *The relative | + | *The relative error with respect to the actual value according to the subtask '''(3)''' is only $0.13\%$. |
| − | *In | + | *In solutions 1 and 2, the dimensions are wrong. |
| − | *In solution 2, there would be no propagation delay if both antennas were the same height. This is | + | *In solution 2, there would be no propagation delay if both antennas were the same height. This is clearly not true. |
| − | '''(5)''' The path loss exponent $\gamma = 2$ | + | '''(5)''' The path loss exponent $\gamma = 2$ implies that the reception power $P_{\rm E}$ decreases quadratically with distance. |
| − | *The signal amplitude thus decreases with $1/d$, | + | *The signal amplitude thus decreases with $1/d$, so for some constant $K$ we have |
:$$k_1 = \frac {K}{d_1} \hspace{0.05cm},\hspace{0.2cm}|k_2| = \frac {K}{d_2} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} | :$$k_1 = \frac {K}{d_1} \hspace{0.05cm},\hspace{0.2cm}|k_2| = \frac {K}{d_2} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} | ||
\frac {|k_2|}{k_1} = \frac {d_1}{d_2}= \frac {10011,039\,{\rm m}}{10014,035\,{\rm m}} \approx 0.99 \hspace{0.05cm}.$$ | \frac {|k_2|}{k_1} = \frac {d_1}{d_2}= \frac {10011,039\,{\rm m}}{10014,035\,{\rm m}} \approx 0.99 \hspace{0.05cm}.$$ | ||
| − | *The two path weights thus only differ in | + | *The two path weights thus only differ in magnitude by about $1\%$. |
| − | * | + | *In addition, the coefficients $k_1$ and $k_2$ have different signs ⇒ <u>Answers 1 and 3</u> are correct. |
{{ML-Fuß}} | {{ML-Fuß}} | ||
| − | [[Category: | + | [[Category:Mobile Communications: Exercises|^2.2 Multi-Path Reception in Wireless Systems^]] |
Latest revision as of 13:37, 23 March 2021
The sketched scenario is considered in which the transmitted signal $s(t)$ reaches the antenna of the receiver via two paths:
- $$r(t) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} r_1(t) + r_2(t) =k_1 \cdot s( t - \tau_1) + k_2 \cdot s( t - \tau_2) \hspace{0.05cm}.$$
Note the following:
- The delays $\tau_1$ and $\tau_2$ of the main and the secondary paths can be calculated from the path lengths $d_1$ and $d_2$ using the speed of light $c = 3 \cdot 10^8 \ \rm m/s$ .
- The amplitude factors $k_1$ and $k_2$ are obtained according to the path loss model with path loss exponent $\gamma = 2$ (free–space attenuation).
- The height of the transmit antenna is $h_{\rm S} = 500 \ \rm m$. The height of the receiving antenna is $h_{\rm E} = 30 \ \rm m$. The antennas are separated by a distance of $d = 10 \ \ \rm km$.
- The reflection on the secondary path causes a phase change of $\pi$, so that the partial signals must be subtracted. This is taken into account by a negative $k_2$ value.
Note:
- This task belongs to the chapter Multi–Path Reception in Mobile Communications.
Questionnaire
Solution
(1) According to Pythagoras:
- $$d_1 = \sqrt{d^2 + (h_{\rm S}- h_{\rm E})^2} = \sqrt{10^2 + (0.5- 0.03)^2} \,\,{\rm km} \hspace{0.1cm} \underline {=10011.039\,{\rm m}} \hspace{0.05cm}.$$
- Actually, specifying such a length with an accuracy of one millimeter is not very useful and contradicts the mentality of an engineer.
- We have done this anyway to be able to check the accuracy of the approximation in subtask (4).
(2) If you fold the reflected beam on the right side of $x_{\rm R}$ downwards (reflection on the ground), you get again a right triangle. From this follows:
- $$d_2 = \sqrt{d^2 + (h_{\rm S}+ h_{\rm E})^2} = \sqrt{10^2 + (0.5+ 0.03)^2} \,\,{\rm km} \hspace{0.1cm} \underline {=10014.035\,{\rm m}} \hspace{0.05cm}.$$
(3) Using the results from (1) and (2), the length and delay differences are:
- $$\Delta d = d_2 - d_1 = \hspace{0.1cm} \underline {=2.996\,{\rm m}} \hspace{0.05cm},\hspace{1cm} \Delta \tau = \frac{\Delta d}{c} = \frac{2.996\,{\rm m}}{3 \cdot 10^8 \,{\rm m/s}} \hspace{0.1cm} \underline {=9.987\,{\rm ns}} \hspace{0.05cm}.$$
(4) With $h_{\rm S} + h_{\rm E} \ll d$ the above equation can be expressed as follows:
- $$d_1 \hspace{-0.1cm} \ = \ \hspace{-0.1cm} d \cdot \sqrt{1 + \frac{(h_{\rm S}- h_{\rm E})^2}{d^2}} \approx d \cdot \left [ 1 + \frac{(h_{\rm S}- h_{\rm E})^2}{2d^2} \right ] \hspace{0.05cm},\hspace{1cm} d_2 \hspace{-0.1cm} \ = \ \hspace{-0.1cm} d \cdot \sqrt{1 + \frac{(h_{\rm S}+ h_{\rm E})^2}{d^2}} \approx d \cdot \left [ 1 + \frac{(h_{\rm S}+ h_{\rm E})^2}{2d^2} \right ] $$
- $$\Rightarrow \hspace{0.3cm} \Delta d = d_2 - d_1 \approx \frac {1}{2d} \cdot \left [ (h_{\rm S}+ h_{\rm E})^2 - (h_{\rm S}- h_{\rm E})^2 \right ] = \frac {2 \cdot h_{\rm S}\cdot h_{\rm E}}{d}\hspace{0.3cm} \Rightarrow \hspace{0.3cm} \Delta \tau = \frac{\Delta d}{c} \approx \frac {2 \cdot h_{\rm S}\cdot h_{\rm E}}{c \cdot d} \hspace{0.05cm}.$$
- So the correct solution is the solution 3. With the given numerical values, we have
- $$\Delta \tau \approx \frac {2 \cdot 500\,{\rm m}\cdot 30\,{\rm m}}{3 \cdot 10^8 \,{\rm m/s} \cdot 10000\,{\rm m}} = 10^{-8}\,{\rm s} = 10\,{\rm ns} \hspace{0.05cm}.$$
- The relative error with respect to the actual value according to the subtask (3) is only $0.13\%$.
- In solutions 1 and 2, the dimensions are wrong.
- In solution 2, there would be no propagation delay if both antennas were the same height. This is clearly not true.
(5) The path loss exponent $\gamma = 2$ implies that the reception power $P_{\rm E}$ decreases quadratically with distance.
- The signal amplitude thus decreases with $1/d$, so for some constant $K$ we have
- $$k_1 = \frac {K}{d_1} \hspace{0.05cm},\hspace{0.2cm}|k_2| = \frac {K}{d_2} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \frac {|k_2|}{k_1} = \frac {d_1}{d_2}= \frac {10011,039\,{\rm m}}{10014,035\,{\rm m}} \approx 0.99 \hspace{0.05cm}.$$
- The two path weights thus only differ in magnitude by about $1\%$.
- In addition, the coefficients $k_1$ and $k_2$ have different signs ⇒ Answers 1 and 3 are correct.