Difference between revisions of "Aufgaben:Exercise 2.2: DC Component of Signals"
From LNTwww
m (Text replacement - "Category:Exercises for Signal Representation" to "Category:Signal Representation: Exercises") |
|||
| Line 3: | Line 3: | ||
}} | }} | ||
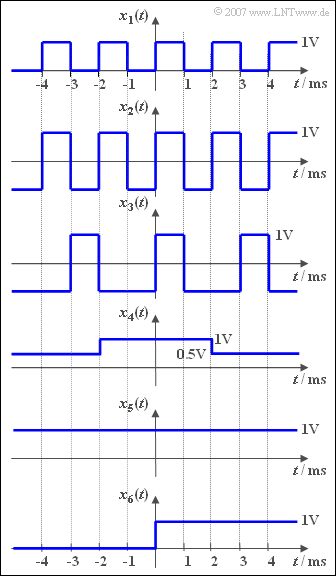
| − | [[File:P_ID273__Sig_A_2_2.png|right|frame| | + | [[File:P_ID273__Sig_A_2_2.png|right|frame|Square wave signal with and without DC component]] |
The graph shows some time signals defined for all times $($from $-\infty$ to $+\infty)$ . For all six sample signals $x_i(t)$ the associated spectral function can be written as: | The graph shows some time signals defined for all times $($from $-\infty$ to $+\infty)$ . For all six sample signals $x_i(t)$ the associated spectral function can be written as: | ||
Revision as of 10:21, 26 March 2021
The graph shows some time signals defined for all times $($from $-\infty$ to $+\infty)$ . For all six sample signals $x_i(t)$ the associated spectral function can be written as:
- $$X_i(f)=A_0\cdot{\rm \delta}(f)+\Delta X_i(f).$$
Here
- $A_0$ is the DC component, and
- $\Delta X_i(f)$ is the spectrum of the residual signal reduced by the DC component $\Delta x_i(t) = x_i(t) - A_0$.
Hint:
- This exercise belongs to the chapter Direct Current Signal - Limit Case of a Periodic Signal.
Questions
Solution
(1) The correct answers are 1, 3, 4, 5 and 6.
- All signals except $x_2(t)$ contain a DC signal component.
(2) Only solution 5 is correct:
- If the DC component $1\text{V}$ is subtracted from the signal $x_5(t)$ , the residual signal $\Delta x_5(t) = x5(t) - 1\text{V}$ is equal to zero.
- Accordignly, the spectral function is $\Delta X_5(f) = 0$.
- For all other time courses $\Delta x_i(t)$ is not equal to zero and thus the associated spectral function $\Delta X_i(f)$ is also not equal to zero.
(3) Given a periodic signal, averaging over a period duration is sufficient to calculate the DC signal component $A_0$ .
- For the sample signal $x_3(t)$ the period duration is $T_0 = 3\,\text{ms}$. This results in the required DC component:$$A_0=\rm \frac{1}{3\,ms}\cdot \big[1\,V\cdot 1\,ms+(-1\,V)\cdot 2\,ms \big] \hspace{0.15cm}\underline{=-0.333\,V}.$$
(4) The signal $x_4(t)$ can be written as: $x_4(t) = 0.5 \,{\rm V} + Δx_4(t)$.
- Here $Δx_4(t)$ denotes a square wave pulse with amplitude $0.5 \,{\rm V} $ and duration $4 \,{\rm ms} $, which due to its finite duration does not contribute to the DC signal component..
- Therefore $A_0 \hspace{0.15cm}\underline{=0.5 \,{\rm V}}$ applies here.
(5) The general equation for calculating the DC signal component is:
- $$A_0=\lim_{T_{\rm M}\to \infty}\frac{1}{T_{\rm M}}\int_{-T_{\rm M}/2}^{+T_{\rm M}/2}x(t)\, {\rm d }t.$$
- If one splits this integral into two partial integrals, one obtains:
- $$A_0=\lim_{T_{\rm M}\to \infty}\frac{1}{T_{\rm M}}\int _{-T_{\rm M}/2}^{0}0 {\rm V} \cdot\, {\rm d } {\it t }+\lim_{T_{\rm M}\to \infty}\frac{1}{T_{\rm M}}\int _{0}^{+T_{\rm M}/2}1 \rm V \ {\rm d }{\it t }.$$
- Only the second term makes a contribution. From this follows again : $A_0 \hspace{0.15cm}\underline{=0.5 \,{\rm V}}$.