Difference between revisions of "Aufgaben:Exercise 2.2Z: Non-Linearities"
From LNTwww
m (Guenter moved page Exercise 2.2Z: Nonlinearities to Exercise 2.2Z: Non-Linearities) |
|
(No difference)
| |
Revision as of 15:57, 12 April 2021
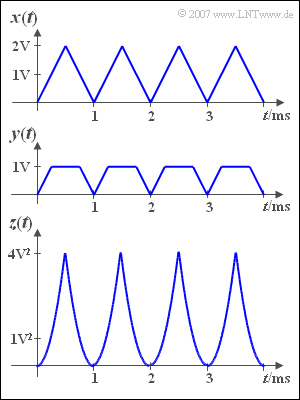
We start from the triangular signal ${x(t)}$ according to the figure above.
If we apply this signal to an amplitude limiter, we get the signal
- $$y(t)=\left\{ {x(t)\atop \rm 1V}{\hspace{0.5cm} {\rm for}\quad x(t)\le \rm 1V \atop {\rm else}}\right..$$
A second non-linearity provides the signal
- $$z(t)=x^2(t).$$
The DC signal components are designated $x_0$, $y_0$ and $z_0$ in the following.
Hint:
- This exercise belongs to the chapter Direct Current Signal - Limit Case of a Periodic Signal.
Questions
Solution
(1) The DC signal $x_0$ is the mean value of the signal ${x(t)}$. Averaging over a period duration $T_0 = 1 \, \text{ms}$ is sufficient. One obtains:
- $$x_0=\frac{1}{T_0}\int^{T_0}_0 x(t)\,{\rm d} t \hspace{0.15cm}\underline{=1\,\rm V}.$$
(2) In half the time ${y(t)} = 1\, \text{V}$, in the other half is is between $0$ and $1\, \text{V}$ with the mean value at $0.5 \,\text{V}$ ⇒ $y_0 \hspace{0.15cm}\underline{= 0.75 \,\text{V}}$.
(3) Due to the periodicity and symmetry, averaging in the range from $0$ bis $T_0/2$ is sufficient.
- With the corresponding characteristic curve, the following then applies::
- $$z_0=\frac{1}{T_0/2}\int^{T_0/2}_0 x^2(t)\,{\rm d}t=\frac{4\rm V^2}{T_0/2}\int^{T_0/2}_0 ({2t}/{T_0})^2\, {\rm d}t={4}/{3}\rm \;V^2 \hspace{0.15cm}\underline{\approx1.333\rm \;V^2}.$$