Difference between revisions of "Aufgaben:Exercise 2.4: Rectified Cosine"
| (35 intermediate revisions by 6 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Signal_Representation/Fourier_Series |
}} | }} | ||
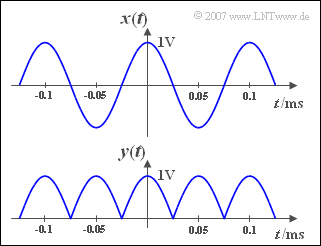
| − | [[File:P_ID300__Sig_A_2_4.png| | + | [[File:P_ID300__Sig_A_2_4.png|right|frame|Cosine and rectified cosine]] |
| − | + | A cosine signal $x(t)$ with amplitude $1\,\rm{V}$ and frequency $f_0= 10\,\rm{kHz}$ is applied to the input of a half-wave rectifier. At its output, the signal $y(t)$ results, which is shown in the graph below. | |
| − | |||
| − | + | In subtasks '''(6)''' and '''(7)''' the error signal $\varepsilon_3(t) = y_3(t) - y(t)$ is also used. This describes the difference between the Fourier series ⇒ $y_3(t)$ limited to only $N = 3$ coefficients and the actual output signal $y(t)$. | |
| − | + | ||
| − | + | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | ''Hints:'' | ||
| + | *This exercise belongs to the chapter [[Signal_Representation/Fourier_Series|Fourier Series]]. | ||
| + | |||
| + | *To solve the problem, you can use the following definite integral $($let $n$ be an integer$)$: | ||
| − | $$\int ^{\pi /2}_{-\pi /2}\cos(u)\cdot\cos(2nu)\,{\rm d}u = (-1)^{n+1}\cdot\frac{2}{4n^2-1}.$$ | + | :$$\int ^{\pi /2}_{-\pi /2}\cos(u)\cdot\cos(2nu)\,{\rm d}u = (-1)^{n+1}\cdot\frac{2}{4n^2-1}.$$ |
| + | |||
| + | *You can find a compact summary of the topic in the (German language) learning video<br> [[Zur_Berechnung_der_Fourierkoeffizienten_(Lernvideo)|Zur Berechnung der Fourierkoeffizienten]] ⇒ "To calculate the Fourier coefficients". | ||
| + | |||
| − | === | + | |
| + | |||
| + | ===Questions=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Which of the following statements are true for the signal $x(t)$ ? |
|type="[]"} | |type="[]"} | ||
| − | + | + | + The period duration is $T_0 = 100 \,µ{\rm s}$. |
| − | + | + | + The DC signal coefficient is $A_0 = 0$. |
| − | + | + | + Of all cosine coefficients $A_n$ exactly one is not equal to zero. |
| − | - | + | - Of all the sine coefficients $B_n$ exactly one is not equal to zero. |
| − | + | + | + The Fourier series $x_3(t)$ does not deviate from the actual signal $x(t)$ . |
| − | { | + | {What is the period duration of the signal $y(t)$? |
|type="{}"} | |type="{}"} | ||
| − | $T_0$ | + | $T_0\ = \ $ { 50 3% } ${\rm µs}$ |
| − | { | + | {Calculate the DC component of the signal $y(t)$. |
|type="{}"} | |type="{}"} | ||
| − | $A_0$ | + | $A_0\ = \ $ { 0.637 3% } ${\rm V}$ |
| − | { | + | {What are the sine coefficients $B_n$? Justify your result. Enter the coefficient $B_2$ as a check. |
|type="{}"} | |type="{}"} | ||
| − | $B_2$ | + | $B_2\ = \ $ { 0. } ${\rm V}$ |
| − | { | + | |
| + | {Now calculate the cosine coefficient $A_n$. Enter the coefficient $A_2$ as a check. | ||
|type="{}"} | |type="{}"} | ||
| − | $A_2$ | + | $A_2\ = \ $ { -0.087--0.083 } ${\rm V}$ |
| + | |||
| − | { | + | {Specify the Fourier series $y_3(t)$ analytically $($limit to $N = 3$ sine and cosine coefficients each$)$. |
| + | <br>How large is the error between this finite Fourier series and the actual signal value at $t = 0$? | ||
|type="{}"} | |type="{}"} | ||
| − | $\ | + | $\varepsilon_3(t= 0)\ = \ $ { 0.0125 3% } ${\rm V}$ |
| − | { | + | {Now calculate the error $\varepsilon_3(t= 25 \,µ{\rm s})$. Interpret this value in comparison to the result from '''(6)'''. |
|type="{}"} | |type="{}"} | ||
| − | $\ | + | $\varepsilon_3(t= 25 \,µ{\rm s})\ = \ $ { 0.091 3% } ${\rm V}$ |
</quiz> | </quiz> | ||
| − | === | + | |
| + | ===Solution=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''1 | + | '''(1)''' All solutions are correct except the fourth: |
| − | + | *From the signal frequency $f_0= 10\,\rm{kHz}$ follows $T_0 = 1/f_0 = 100\,µ\text{s}$. | |
| + | *The cosine signal is mean–free $(A_0 = 0)$ and it is completely described by a single cosine coefficient – namely $A_1$ . | ||
| + | *All sine coefficients are $B_n \equiv 0$, since $x(t)$ is an even function. | ||
| + | *The Fourier series representation $x_3(t)$ reproduces $x(t)$ without error. | ||
| + | |||
| + | |||
| − | '''2 | + | '''(2)''' Due to the double path rectification, the period duration is now half the value: $T_0 \hspace{0.1cm}\underline{= 50\,µ\text{s}}$. |
| + | *For all subsequent points, the specification $T_0$ refers to this value, i.e. to the period of the signal $y(t)$. | ||
| − | '''3 | + | |
| + | |||
| + | '''(3)''' In the range from $–T_0/2$ to $+T_0/2 \ (–25\,µ\text{s} \ \text{...} +25\,µ\text{s})$ is $y(t) = x(t)$. With $f_x= 10\,\rm{kHz} = 1/(2T_0)$ therefore applies to this section: | ||
| − | $$y(t)={\rm 1V}\cdot\cos(2{\pi} f_0\hspace{0.05cm}t)={\rm 1V}\cdot\cos(\pi\ | + | :$$y(t)={\rm 1V}\cdot\cos(2{\pi} f_0\hspace{0.05cm}t)={\rm 1V}\cdot\cos(\pi \cdot {t}/{T_0}).$$ |
| − | + | *This results in the following for the DC coefficient: | |
| − | $$A_0=\frac{1}{T_0}\int^{T_0/2}_{-T_0/2}y(t)\,{\rm d} t=\frac{1}{T_0}\int^{T_0/2}_{-T_0/2}{\rm 1V}\cdot\cos(\pi\ | + | :$$A_0=\frac{1}{T_0}\int^{T_0/2}_{-T_0/2}y(t)\,{\rm d} t=\frac{1}{T_0}\int^{T_0/2}_{-T_0/2}{\rm 1V}\cdot\cos(\pi\cdot {t}/{T_0})\,{\rm d}t.$$ |
| − | + | *With the substitution $u = \pi \cdot t/T_0$ one obtains: | |
| − | $$A_0=\left. \frac{ {\rm 1V}}{\pi}\int_{-\pi /2}^{\pi/2}\cos(u)\,{\rm d}u=\frac{ {\rm 1V}}{\pi}\sin(u)\; \right| _{-\pi/2}^{\pi/2}=\frac{ {\rm 1V}\cdot 2}{\pi} \hspace{0.15cm}\underline{\approx 0.637\;{\rm V}}.$$ | + | :$$A_0=\left. \frac{ {\rm 1V}}{\pi}\int_{-\pi /2}^{\pi/2}\cos(u)\,{\rm d}u=\frac{ {\rm 1V}}{\pi}\sin(u)\; \right| _{-\pi/2}^{\pi/2}=\frac{ {\rm 1V}\cdot 2}{\pi} \hspace{0.15cm}\underline{\approx 0.637\;{\rm V}}.$$ |
| + | |||
| + | |||
| + | '''(4)''' Since $y(–t) = y(t)$ holds, all sine coefficients $B_n = 0$. Thus $B_2 \hspace{0.1cm}\underline{= 0}$ also holds. | ||
| + | |||
| − | |||
| − | '''5 | + | '''(5)''' For the coefficients $A_n$ applies with the substitution $u = \pi \cdot t/T_0$ according to the given integral: |
| − | $$A_n = \frac{2{\rm V}}{T_0}\int_{-T_0/2}^{T_0/2}\cos(\pi\frac{t}{T_0})\cdot \cos(n\cdot 2\pi\frac{t}{T_0})\,{\rm d}t = \frac{2{\rm V}}{\pi}\int_{-\pi/2}^{\pi/2}\cos(u)\cdot \cos(2n u)\,{\rm d}u \ | + | :$$A_n = \frac{2{\rm V}}{T_0}\int_{-T_0/2}^{T_0/2}\cos(\pi\frac{t}{T_0})\cdot \cos(n\cdot 2\pi\frac{t}{T_0})\,{\rm d}t = \frac{2{\rm V}}{\pi}\int_{-\pi/2}^{\pi/2}\cos(u)\cdot \cos(2n u)\,{\rm d}u \quad |
\Rightarrow \quad A_n = \left( { - 1} \right)^{n + 1} \frac{{4\;{\rm{V}}}}{{{\rm{\pi }}\left( {4n^2 - 1} \right)}}.$$ | \Rightarrow \quad A_n = \left( { - 1} \right)^{n + 1} \frac{{4\;{\rm{V}}}}{{{\rm{\pi }}\left( {4n^2 - 1} \right)}}.$$ | ||
| − | + | The coefficient $A_2$ is thus equal to $-4 \,\text{V}/(15\pi) \hspace{0.1cm}\underline{\approx -\hspace{0.05cm}0.085 \, \text{V}}$. | |
| + | |||
| + | |||
| + | |||
| + | '''(6)''' For the finite Fourier series with $N = 3$ the following applies in general: | ||
| + | |||
| + | :$$y_3(t)=\frac{2{\rm V}}{\pi} \cdot \left [ 1+{2}/{3} \cdot \cos(\omega_0t)-{2}/{15}\cdot \cos(2\omega_0t)+{2}/{35}\cdot \cos(3\omega_0t) \right ].$$ | ||
| + | |||
| + | At time $t = 0$: $y_3(0) \approx 1.0125 \ \rm V$; thus the error is $\varepsilon_3(t = 0) \hspace{0.15cm}\underline{= 0.0125 \,\text{V}}$ . | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | '''7 | + | '''(7)''' The time $t = 25\,µ\text{s}$ corresponds to half the period of the signal $y(t)$. The following applies here because of $\omega_0 \cdot T_0 = 2\pi$: |
| − | $$ | + | :$$y_3(T_0/2) = \frac{2{\rm V}}{\pi} \left [1+\frac{2}{3} \cdot \cos({\pi}) -\frac{2}{15}\cdot \cos(2\pi)+\frac{2}{35}\cdot \cos(3\pi)\right ]= \frac{2{\rm V}}{\pi}\left [1-\frac{2}{3}-\frac{2}{15}-\frac{2}{35}\right ] = \frac{2{\rm V}}{7\pi}\approx 0.091{\rm V}.$$ |
| − | + | *Since $y(T_0/2) = 0$ this also results in $\varepsilon_3(T_0/2) \hspace{0.15cm}\underline{\approx 0.091\,{\rm V}}$. | |
| + | *This error is larger than the error at $t = 0$ by more than a factor of $7$, since $y(t)$ has more high-frequency components at $t = T_0/2$ $($peak-shaped course$)$. | ||
| + | *If it is required that the error $\varepsilon_3(T_0/2)$ be smaller than $0.01$ then at least $32$ Fourier coefficients would have to be taken into account. | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
__NOEDITSECTION__ | __NOEDITSECTION__ | ||
| − | [[Category: | + | [[Category:Signal Representation: Exercises|^2.4 Fourier Series^]] |
Latest revision as of 13:24, 15 April 2021
A cosine signal $x(t)$ with amplitude $1\,\rm{V}$ and frequency $f_0= 10\,\rm{kHz}$ is applied to the input of a half-wave rectifier. At its output, the signal $y(t)$ results, which is shown in the graph below.
In subtasks (6) and (7) the error signal $\varepsilon_3(t) = y_3(t) - y(t)$ is also used. This describes the difference between the Fourier series ⇒ $y_3(t)$ limited to only $N = 3$ coefficients and the actual output signal $y(t)$.
Hints:
- This exercise belongs to the chapter Fourier Series.
- To solve the problem, you can use the following definite integral $($let $n$ be an integer$)$:
- $$\int ^{\pi /2}_{-\pi /2}\cos(u)\cdot\cos(2nu)\,{\rm d}u = (-1)^{n+1}\cdot\frac{2}{4n^2-1}.$$
- You can find a compact summary of the topic in the (German language) learning video
Zur Berechnung der Fourierkoeffizienten ⇒ "To calculate the Fourier coefficients".
Questions
Solution
- From the signal frequency $f_0= 10\,\rm{kHz}$ follows $T_0 = 1/f_0 = 100\,µ\text{s}$.
- The cosine signal is mean–free $(A_0 = 0)$ and it is completely described by a single cosine coefficient – namely $A_1$ .
- All sine coefficients are $B_n \equiv 0$, since $x(t)$ is an even function.
- The Fourier series representation $x_3(t)$ reproduces $x(t)$ without error.
(2) Due to the double path rectification, the period duration is now half the value: $T_0 \hspace{0.1cm}\underline{= 50\,µ\text{s}}$.
- For all subsequent points, the specification $T_0$ refers to this value, i.e. to the period of the signal $y(t)$.
(3) In the range from $–T_0/2$ to $+T_0/2 \ (–25\,µ\text{s} \ \text{...} +25\,µ\text{s})$ is $y(t) = x(t)$. With $f_x= 10\,\rm{kHz} = 1/(2T_0)$ therefore applies to this section:
- $$y(t)={\rm 1V}\cdot\cos(2{\pi} f_0\hspace{0.05cm}t)={\rm 1V}\cdot\cos(\pi \cdot {t}/{T_0}).$$
- This results in the following for the DC coefficient:
- $$A_0=\frac{1}{T_0}\int^{T_0/2}_{-T_0/2}y(t)\,{\rm d} t=\frac{1}{T_0}\int^{T_0/2}_{-T_0/2}{\rm 1V}\cdot\cos(\pi\cdot {t}/{T_0})\,{\rm d}t.$$
- With the substitution $u = \pi \cdot t/T_0$ one obtains:
- $$A_0=\left. \frac{ {\rm 1V}}{\pi}\int_{-\pi /2}^{\pi/2}\cos(u)\,{\rm d}u=\frac{ {\rm 1V}}{\pi}\sin(u)\; \right| _{-\pi/2}^{\pi/2}=\frac{ {\rm 1V}\cdot 2}{\pi} \hspace{0.15cm}\underline{\approx 0.637\;{\rm V}}.$$
(4) Since $y(–t) = y(t)$ holds, all sine coefficients $B_n = 0$. Thus $B_2 \hspace{0.1cm}\underline{= 0}$ also holds.
(5) For the coefficients $A_n$ applies with the substitution $u = \pi \cdot t/T_0$ according to the given integral:
- $$A_n = \frac{2{\rm V}}{T_0}\int_{-T_0/2}^{T_0/2}\cos(\pi\frac{t}{T_0})\cdot \cos(n\cdot 2\pi\frac{t}{T_0})\,{\rm d}t = \frac{2{\rm V}}{\pi}\int_{-\pi/2}^{\pi/2}\cos(u)\cdot \cos(2n u)\,{\rm d}u \quad \Rightarrow \quad A_n = \left( { - 1} \right)^{n + 1} \frac{{4\;{\rm{V}}}}{{{\rm{\pi }}\left( {4n^2 - 1} \right)}}.$$
The coefficient $A_2$ is thus equal to $-4 \,\text{V}/(15\pi) \hspace{0.1cm}\underline{\approx -\hspace{0.05cm}0.085 \, \text{V}}$.
(6) For the finite Fourier series with $N = 3$ the following applies in general:
- $$y_3(t)=\frac{2{\rm V}}{\pi} \cdot \left [ 1+{2}/{3} \cdot \cos(\omega_0t)-{2}/{15}\cdot \cos(2\omega_0t)+{2}/{35}\cdot \cos(3\omega_0t) \right ].$$
At time $t = 0$: $y_3(0) \approx 1.0125 \ \rm V$; thus the error is $\varepsilon_3(t = 0) \hspace{0.15cm}\underline{= 0.0125 \,\text{V}}$ .
(7) The time $t = 25\,µ\text{s}$ corresponds to half the period of the signal $y(t)$. The following applies here because of $\omega_0 \cdot T_0 = 2\pi$:
- $$y_3(T_0/2) = \frac{2{\rm V}}{\pi} \left [1+\frac{2}{3} \cdot \cos({\pi}) -\frac{2}{15}\cdot \cos(2\pi)+\frac{2}{35}\cdot \cos(3\pi)\right ]= \frac{2{\rm V}}{\pi}\left [1-\frac{2}{3}-\frac{2}{15}-\frac{2}{35}\right ] = \frac{2{\rm V}}{7\pi}\approx 0.091{\rm V}.$$
- Since $y(T_0/2) = 0$ this also results in $\varepsilon_3(T_0/2) \hspace{0.15cm}\underline{\approx 0.091\,{\rm V}}$.
- This error is larger than the error at $t = 0$ by more than a factor of $7$, since $y(t)$ has more high-frequency components at $t = T_0/2$ $($peak-shaped course$)$.
- If it is required that the error $\varepsilon_3(T_0/2)$ be smaller than $0.01$ then at least $32$ Fourier coefficients would have to be taken into account.