Aufgaben:Exercise 2.5Z: Square Wave

• Return to book

Various square wave signals

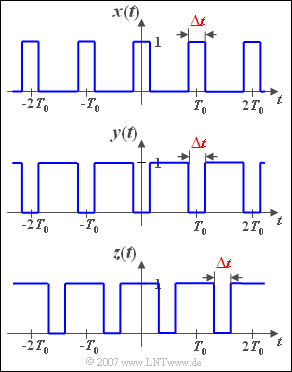
The signal  $x(t)$  periodic with time  $T_0$  is described by the single parameter  $\Delta t$;  let the amplitude of the square-wave pulses be  $1$ in each case.  Since  $x(t)$  is even, all sine coefficients  $B_n = 0$.

The DC signal coefficient is  $A_0 = \Delta t/T_0$  and the following applies to the cosine coefficients:

$$A_n=\frac{2}{n\pi}\cdot \sin(n\pi \Delta t/T_0).$$

In subtasks  (1)  and  (2)  the signal  $x(t)$  is analysed for the two parameter values  $\Delta t/T_0 = 0.5$  and  $\Delta t/T_0 = 0.25$  respectively.

Then we consider the two signals  $y(t)$  and  $z(t)$, each with  $\Delta t/T_0 = 0.25$. There is a fixed relationship between these signals and  $x(t)$  which can be exploited for the calculation.

Hints:

• This exercise belongs to the chapter  Fourier Series.
• You can find a compact summary of the topic in the two learning videos

Zur Berechnung der Fourierkoeffizienten  ⇒   "To calculate the Fourier coefficients",

Eigenschaften der Fourierreihendarstellung   ⇒   "Properties of the Fourier series representation".

Questions

1

Which statements are true for the signal  $x(t)$  with  $\Delta t/T_0 = 0.5$?

	The spectral function  ${X(f)}$  contains a Dirac function at  $f = 0$  with the weight  $0.5$.
	The spectral function  ${X(f)}$  contains Dirac lines at all multiples of the base frequency  $f_0 = 1/T_0$.
	The spectral function  ${X(f)}$  contains Dirac lines at odd multiples of the base frequency   $f_0$.
	The spectral line at  $f_0$  has the weight  $2/\pi = 0.636$.
	The spectral line at  $–\hspace{-0.1cm}f_0$  has the weight  $1/\pi = 0.318$.

2

Which statements are true for the signal  $x(t)$  with  $\Delta t/T_0 = 0.25$?

	The spectral function  ${X(f)}$  contains Dirac lines at all odd multiples of the base frequency  $f_0$.
	${X(f)}$  has Dirac lines at  $\pm2f_0$,  $\pm6f_0$,  $\pm10f_0$, etc.
	${X(f)}$  has Dirac lines at  $\pm4f_0$,  $\pm8f_0$,  $\pm12f_0$, etc.
	The Dirac line at  $2f_0$  has the weight  $1/(2\pi) = 0.159$.

3

What is the DC coefficient of the signal  ${y(t)}$?

$y(t)$:   $A_0 \ = \ $

4

What is the relationship between the signals  $x(t)$  and  ${y(t)}$?  With the help of these considerations, give the Fourier coefficients of  ${y(t)}$.
What are the coefficients  $A_1$  and  $A_2$  of this signal?

$y(t)$:   $A_1\ = \ $

$\hspace{1cm}A_2 \ = \ $

5

What is the relationship between the signals  ${y(t)}$  and  ${z(t)}$?  What are the coefficients  $A_1$  and  $A_2$  of the signal  ${z(t)}$?
Check the result using the given coefficients of the signal  $x(t)$.

$z(t)$:   $A_1 \ = \ $

$\hspace{1cm}A_2 \ = \ $

Solution

Solution

(1)  Statements 1, 3 and 5 are correct:

• The spectral function contains a Dirac line at  $f = 0$  with weight  $0.5$  (DC component)  as well as further spectral lines at odd multiples  ($n = \pm1, \pm3, \pm5,\text{...}$ of $f_0$.
• The weights at  $\pm f_0$ are $A_1/2 = 1/\pi = 0.318$  in each case.

(2)  Statements 1, 2 and 4 are correct:

• Spectral lines exist at all odd multiples of the basic frequency, and additionally at the  $2–{\rm fold}$,  $6–{\rm fold}$  and  $10–{\rm fold}$.
• For example  $A_1 = 1/\pi = 0.450$.  The Dirac line at  $2f_0$  thus has the weight  $A_2/2 = 1/(2\pi) = 0.159$.
• For  $n = 4$,  $n = 8$, etc., on the other hand, the coefficients  $A_n = 0$, since the following holds for the sine function:   $\sin(\pi) = \sin(2\pi) =\text{ ...} = 0$.

(3)  From the graphical representation of the signal  ${y(t)}$  it is clear that  $A_0 = 0.75$  must apply.  The same result can be obtained using the relationship:

$$A_0^{(y)}=1-A_0^{(x)}=1-0.25\hspace{0.15cm}\underline{=0.75}.$$

(4)  The following applies:  ${y(t)} = 1 - x(t)$.  For  $n \neq 0$  the Fourier coefficients are the same as for the signal  $x(t)$, but with negative signs.  In particular:

$$A_1^{(y)} = -A_1^{(x)}=-{2}/{\pi} \cdot \sin({\pi}/{4})= -{\sqrt2}/{\pi}\hspace{0.15cm}\underline{\approx -0.450},$$

$$A_2^{(y)} = -A_2^{(x)}=-{1}/{\pi}\hspace{0.15cm}\underline{ \approx - 0.318}.$$

(5)  ${z(t)} = y(t - T_0/2)$ applies.  With the Fourier series representation of  ${y(t)}$  it follows:

$$z(t)=A_0+A_1^{(y)}\cos(\omega_0(t-\frac{T_0}{2}))+A_2^{(y)}\cos(2\omega_0(t-\frac{T_0}{2}))+A_3^{(y)}\cos(3\omega_0(t-\frac{T_0}{2}))+\ldots$$

$$\Rightarrow \quad z(t)=A_0-A_1^{(y)}\cos(\omega_0 t)+A_2^{(y)}\cos(2\omega_0 t)-A_3^{(y)}\cos(3\omega_0 t)+\text{...}$$

Thus one obtains:

$$A_1^{(z)}=-A_1^{(y)}={\sqrt2}/{\pi}\hspace{0.15cm}\underline{=+0.450}, \hspace {0.5cm} A_2^{(z)}=A_2^{(y)}=-{1}/{\pi}\hspace{0.15cm}\underline{=-0.318}.$$

The same result is obtained starting from the given coefficients with  $\Delta t/T_0 = 0.75$:

$$A_1^{(z)}={2}/{\pi} \cdot \sin({3}/{4}\cdot \pi)={\sqrt2}/{\pi}, \hspace {0.5cm}A_2^{(z)}= {1}/{\pi} \cdot \sin({3}/{2} \cdot \pi) =-{1}/{\pi}.$$