Difference between revisions of "Aufgaben:Exercise 2.6: Complex Fourier Series"
From LNTwww
| (2 intermediate revisions by the same user not shown) | |||
| Line 5: | Line 5: | ||
[[File:P_ID312__Sig_A_2_6.png|right|frame|Various periodic triangular signals]] | [[File:P_ID312__Sig_A_2_6.png|right|frame|Various periodic triangular signals]] | ||
| − | We consider the signal $x(t)$, defined by the two parameters $T_0$ and $T_1$ where $T_1 \leq T_0$ should always apply. For the complex Fourier coefficients | + | We consider the signal $x(t)$, defined by the two parameters $T_0$ and $T_1$ where $T_1 \leq T_0$ should always apply. For the complex Fourier coefficients |
:$$D_n=\frac{1}{T_0} \cdot \int_0^{T_0}x(t)\cdot\rm e^{-\rm j\it n\omega_0t}\,{\rm d} \it t$$ | :$$D_n=\frac{1}{T_0} \cdot \int_0^{T_0}x(t)\cdot\rm e^{-\rm j\it n\omega_0t}\,{\rm d} \it t$$ | ||
| Line 11: | Line 11: | ||
of this signal are obtained after mathematical transformations: | of this signal are obtained after mathematical transformations: | ||
| − | :$$D_n=\frac{T_0/T_1} {(2\pi n)^2} \cdot \ | + | :$$D_n=\frac{T_0/T_1} {(2\pi n)^2} \cdot \big(1-{\rm e}^{-{\rm j} 2\pi nT_1/T_0}\big)-\frac{\rm j}{2\pi n}.$$ |
*The parameter set dealt with in subtasks '''(1)''' and '''(3)''' $($with $T_1 = T_0/2)$ is represented as the signal $x(t)$ . | *The parameter set dealt with in subtasks '''(1)''' and '''(3)''' $($with $T_1 = T_0/2)$ is represented as the signal $x(t)$ . | ||
*For $T_1 = T_0$ ⇒ subtask '''(2)''' the function $y(t)$ results. | *For $T_1 = T_0$ ⇒ subtask '''(2)''' the function $y(t)$ results. | ||
| − | *In subtask '''(4)''' the signal $z(t)$ is considered. Its Fourier coefficients are: | + | *In subtask '''(4)''' the signal $z(t)$ is considered. Its Fourier coefficients are: |
:$$A_0=1/4,\hspace{1cm} | :$$A_0=1/4,\hspace{1cm} | ||
| Line 28: | Line 28: | ||
''Hints:'' | ''Hints:'' | ||
| − | *This exercise refers to the page [[Signal_Representation/Fourier_Series# | + | *This exercise refers to the page [[Signal_Representation/Fourier_Series#Complex_Fourier_series|Complex Fourier series]]. |
| Line 39: | Line 39: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Calculate the coefficient $D_0$ and show that it is always real. What value results for $T_1 = T_0/2$, i.e. for the signal $x(t)$? | + | {Calculate the coefficient $D_0$ and show that it is always real. What value results for $T_1 = T_0/2$, i.e. for the signal $x(t)$? |
|type="{}"} | |type="{}"} | ||
$D_0^{(x)}\ = \ $ { 0.25 3% } | $D_0^{(x)}\ = \ $ { 0.25 3% } | ||
| − | {Calculate the complex Fourier coefficients $D_n^{(y)}$ for $n \neq 0$ for the special case $T_1 = T_0$ corresponding to the signal $y(t)$ . <br>What are the coefficients $A_n^{(y)}$ and $B_n^{(y)}$, especially for $n = 1$? | + | {Calculate the complex Fourier coefficients $D_n^{(y)}$ for $n \neq 0$ for the special case $T_1 = T_0$ corresponding to the signal $y(t)$ . <br>What are the coefficients $A_n^{(y)}$ and $B_n^{(y)}$, especially for $n = 1$? |
|type="{}"} | |type="{}"} | ||
$A_1^{(y)}\ = \ $ { 0. } | $A_1^{(y)}\ = \ $ { 0. } | ||
$B_1^{(y)}\ = \ $ { 0.318 3% } | $B_1^{(y)}\ = \ $ { 0.318 3% } | ||
| − | {Now calculate the coefficients $A_n^{(x)}$ and $B_n^{(x)}$ for the signal $x(t)$ with $T_1 = T_0/2$ for $n \neq 0$. What are the values for $A_1^{(x)}$ and $B_1^{(x)}$? | + | {Now calculate the coefficients $A_n^{(x)}$ and $B_n^{(x)}$ for the signal $x(t)$ with $T_1 = T_0/2$ for $n \neq 0$. What are the values for $A_1^{(x)}$ and $B_1^{(x)}$? |
|type="{}"} | |type="{}"} | ||
$A_1^{(x)}\ = \ $ { 0.203 3% } | $A_1^{(x)}\ = \ $ { 0.203 3% } | ||
| Line 73: | Line 73: | ||
:$${\rm Im}[D_n] =\frac{T_0/T_1}{(2\pi n)^2} \cdot \sin(2\pi nT_1/T_0)-\frac{1}{2\pi n}.$$ | :$${\rm Im}[D_n] =\frac{T_0/T_1}{(2\pi n)^2} \cdot \sin(2\pi nT_1/T_0)-\frac{1}{2\pi n}.$$ | ||
| − | *With the approximation $\text{sin}(\alpha ) \approx \alpha$ valid for small $\alpha$ | + | *With the approximation $\text{sin}(\alpha ) \approx \alpha$ valid for small $\alpha$–values one obtains for the imaginary part: |
:$${\rm Im}[D_n] =\frac{T_0/T_1}{(2\pi n)^2}\cdot(2\pi nT_1/T_0)-\frac{1}{2\pi n}=0.$$ | :$${\rm Im}[D_n] =\frac{T_0/T_1}{(2\pi n)^2}\cdot(2\pi nT_1/T_0)-\frac{1}{2\pi n}=0.$$ | ||
| Line 98: | Line 98: | ||
:$$D_n^{(y)}=\frac{-\rm j}{2\pi n}={1}/{2} \cdot (A_n- {\rm j} \cdot B_n).$$ | :$$D_n^{(y)}=\frac{-\rm j}{2\pi n}={1}/{2} \cdot (A_n- {\rm j} \cdot B_n).$$ | ||
| − | *The coefficient comparison yields $A_n^{(y)} = 0$ and $B_n^{(y)} = 1/(\pi n)$. In particular $A_1^{(y)} \hspace{0.1cm}\underline{= 0}$ und $B_1^{(y)}\hspace{0.1cm}\underline{ \approx 0.318}$. | + | *The coefficient comparison yields $A_n^{(y)} = 0$ and $B_n^{(y)} = 1/(\pi n)$. In particular $A_1^{(y)} \hspace{0.1cm}\underline{= 0}$ und $B_1^{(y)}\hspace{0.1cm}\underline{ \approx 0.318}$. |
*As expected, $B_{-n}^{(y)} = -B_n^{(y)}$ always holds. | *As expected, $B_{-n}^{(y)} = -B_n^{(y)}$ always holds. | ||
| Line 122: | Line 122: | ||
'''(4)''' The correct <u>solutions are 2, 4 and 5</u>: | '''(4)''' The correct <u>solutions are 2, 4 and 5</u>: | ||
| − | *The signal $x(t)$ is equal to the difference between $y(t)$ and $z(t)$. Since $z(t)$ is an even and $y(t)$ an odd function, the cosine coefficients $A_n$ are determined by the coefficients of the signal $z(t)$ alone, but with negative signs. | + | *The signal $x(t)$ is equal to the difference between $y(t)$ and $z(t)$. Since $z(t)$ is an even and $y(t)$ an odd function, the cosine coefficients $A_n$ are determined by the coefficients of the signal $z(t)$ alone, but with negative signs. |
| − | *The sine coefficients $B_n$ completely agree with those of $y(t)$ | + | *The sine coefficients $B_n$ completely agree with those of $y(t)$. |
*The DC component of $x(t)$ results from the difference of the two DC components of $y(t)$ und $z(t)$: | *The DC component of $x(t)$ results from the difference of the two DC components of $y(t)$ und $z(t)$: | ||
:$$A_0 = 0.5 - 0.25 = 0.25.$$ | :$$A_0 = 0.5 - 0.25 = 0.25.$$ | ||
Latest revision as of 10:49, 16 April 2021
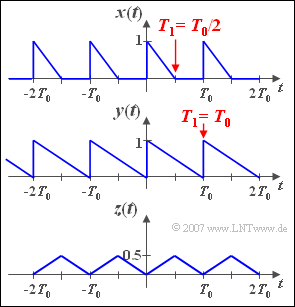
We consider the signal $x(t)$, defined by the two parameters $T_0$ and $T_1$ where $T_1 \leq T_0$ should always apply. For the complex Fourier coefficients
- $$D_n=\frac{1}{T_0} \cdot \int_0^{T_0}x(t)\cdot\rm e^{-\rm j\it n\omega_0t}\,{\rm d} \it t$$
of this signal are obtained after mathematical transformations:
- $$D_n=\frac{T_0/T_1} {(2\pi n)^2} \cdot \big(1-{\rm e}^{-{\rm j} 2\pi nT_1/T_0}\big)-\frac{\rm j}{2\pi n}.$$
- The parameter set dealt with in subtasks (1) and (3) $($with $T_1 = T_0/2)$ is represented as the signal $x(t)$ .
- For $T_1 = T_0$ ⇒ subtask (2) the function $y(t)$ results.
- In subtask (4) the signal $z(t)$ is considered. Its Fourier coefficients are:
- $$A_0=1/4,\hspace{1cm} A_n=\left\{ \begin{array}{cl} {\frac{\displaystyle-2}{\displaystyle(\pi n)^2}} & {\rm for\; even\; \it n \rm ,} \\ 0 & {\rm for\; odd\; \it n,} \end{array}\right. $$
- $$B_n=0\; \;\; \rm{ f\ddot{u}r\; alle\; \it n.}$$
Hints:
- This exercise refers to the page Complex Fourier series.
Questions
Solution
(1) With Euler's theorem, the complex Fourier coefficient $D_n$ can be represented as follows:
- $${\rm Re} [D_n] =\frac{T_0/T_1}{(2\pi n)^2}\cdot(1-\cos(2\pi nT_1/T_0)),$$
- $${\rm Im}[D_n] =\frac{T_0/T_1}{(2\pi n)^2} \cdot \sin(2\pi nT_1/T_0)-\frac{1}{2\pi n}.$$
- With the approximation $\text{sin}(\alpha ) \approx \alpha$ valid for small $\alpha$–values one obtains for the imaginary part:
- $${\rm Im}[D_n] =\frac{T_0/T_1}{(2\pi n)^2}\cdot(2\pi nT_1/T_0)-\frac{1}{2\pi n}=0.$$
- For the real part one obtains with $\text{cos}(\alpha) \approx 1 – \alpha^{2}/2$:
- $${\rm Re}[D_n] =\frac{T_0/T_1}{(2\pi n)^2}\frac{(2\pi nT_1/T_0)^2}{2}=\frac{T_1/T_0}{2}.$$
- For $T_1 = T_0/2$ it follows that the DC signal coefficient $D_0^{(x)} \hspace{0.1cm}\underline{= 0.25}$.
- With $T_1 = T_0$ it results in $D_0^{(y)} = 0.5$.
- A comparison with the signals $x(t)$ and $y(t)$ on the data page show the correctness of these results.
(2) It is now assumed $n \neq 0$ . With $T_1 = T_0$ one obtains for the real part because of $\text{cos}(2\pi n) = 1$:
- $${\rm Re}[D_n^{(y)}] =\frac{1}{(2\pi n)^2}\cdot(1-\cos(2\pi n))=0.$$
- The imagnary part is:
- $${\rm Im}[D_n^{(y)}] =\frac{1}{(2\pi n)^2}\cdot(\sin(2\pi n))-\frac{1}{2\pi n}.$$
- Because $\text{sin}(2\pi n) = 0$ it follows that ${\rm Im}[D_n] =-{1}/({2\pi n}).$ Thus
- $$D_n^{(y)}=\frac{-\rm j}{2\pi n}={1}/{2} \cdot (A_n- {\rm j} \cdot B_n).$$
- The coefficient comparison yields $A_n^{(y)} = 0$ and $B_n^{(y)} = 1/(\pi n)$. In particular $A_1^{(y)} \hspace{0.1cm}\underline{= 0}$ und $B_1^{(y)}\hspace{0.1cm}\underline{ \approx 0.318}$.
- As expected, $B_{-n}^{(y)} = -B_n^{(y)}$ always holds.
(3) From the general equation calculated in subtask (1) it follows with $T_1/T_0 = 1/2$:
- $$D_n^{(x)}=\frac{2}{(2\pi n)^2}(1-\cos(\pi n))+{\rm j}\cdot \left[\frac{2\sin(\pi n)}{(2\pi n)^2}-\frac{1}{(2\pi n)}\right].$$
- From this one obtains the cosine coefficients
- $$A_n^{(x)}={2}\cdot{\rm Re}[D_n] =\left\{ \begin{array}{cl} {\frac{\displaystyle 2}{\displaystyle(\pi n)^2}} & {\rm for\; odd\; \it n ,} \\ 0 & {\rm for\; even\;\it n.} \end{array}\right. $$
- The sine coefficients are:
- $$B_n^{(x)}=-2\cdot{\rm Im}[D_n] =\frac{1}{\pi n}.$$
- Here it is taken into account that for all integer values of $n$ the function $\text{sin}(n\pi ) = 0$ . The first real coefficients are as follows
- $$A_1^{(x)} = 2/\pi^{2} \hspace{0.1cm}\underline{\approx 0.203},$$
- $$B_1 = 1/\pi \hspace{0.1cm}\underline{\approx 0.318}.$$
(4) The correct solutions are 2, 4 and 5:
- The signal $x(t)$ is equal to the difference between $y(t)$ and $z(t)$. Since $z(t)$ is an even and $y(t)$ an odd function, the cosine coefficients $A_n$ are determined by the coefficients of the signal $z(t)$ alone, but with negative signs.
- The sine coefficients $B_n$ completely agree with those of $y(t)$.
- The DC component of $x(t)$ results from the difference of the two DC components of $y(t)$ und $z(t)$:
- $$A_0 = 0.5 - 0.25 = 0.25.$$