Difference between revisions of "Aufgaben:Exercise 3.1Z: Spectrum of the Triangular Pulse"
From LNTwww
m (Text replacement - "Signal_Representation/Fouriertransformation_und_-rücktransformation" to "Signal_Representation/Fourier_Transform_and_Its_Inverse") |
|||
| (10 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Signal_Representation/Fourier_Transform_and_Its_Inverse |
}} | }} | ||
| − | [[File:P_ID493__Sig_Z_3_1_neu.png|right|frame| | + | [[File:P_ID493__Sig_Z_3_1_neu.png|right|frame|Triangular pulse]] |
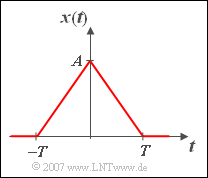
| − | + | A triangular pulse ${x(t)}$ is considered, which is described in the range $–T ≤ t ≤ T$ by the following equation: | |
:$$x(t) = A \cdot \left( {1 - {\left| \hspace{0.05cm}t \hspace{0.05cm}\right|}/{T}} \right).$$ | :$$x(t) = A \cdot \left( {1 - {\left| \hspace{0.05cm}t \hspace{0.05cm}\right|}/{T}} \right).$$ | ||
| − | + | Let the pulse amplitude be $A = 1\, \text{V}$ and the time parameter $T = 1 \text{ ms}$. For all times $|\hspace{0.05cm} t \hspace{0.05cm} | > T$ ⇒ ${x(t)} = 0$. | |
| − | + | To calculate the spectral function ${X(f)}$ you can exploit the following properties: | |
| − | * | + | * The time function is even and thus the spectral function is real: |
| − | :$$X\left( f \right) = \int_{ - \infty }^{ + \infty } {x(t)} \cdot {\rm e}^{{\rm j}2\pi ft} {\rm d}t = 2 \cdot \int_0^{ \infty } {x(t)} \cdot \cos \left( {2\pi ft} \right){\rm d}t.$$ | + | :$$X\left( f \right) = \int_{ - \infty }^{ + \infty } {x(t)} \cdot {\rm e}^{{\rm j}2\pi ft} {\rm d}t = 2 \cdot \int_0^{ \infty } {x(t)} \cdot \cos \left( {2\pi ft} \right)\ {\rm d}t.$$ |
| − | * | + | * For $|\hspace{0.05cm} t \hspace{0.05cm} | > T$ ⇒ ${x(t)}$ has no components: |
| − | : | ||
| + | :$$X\left( f \right) = 2 \cdot \int_0^T {x(t)} \cdot \cos \left( {2\pi ft} \right)\ {\rm d}t.$$ | ||
| Line 22: | Line 22: | ||
| − | '' | + | |
| − | * | + | ''Hints:'' |
| − | * | + | *This exercise belongs to the chapter [[Signal_Representation/Fourier_Transform_and_Its_Inverse|Fourier Transform and its Inverse]]. |
| + | *Further information on this topic can be found in the (German language) learning video [[Kontinuierliche_und_diskrete_Spektren_(Lernvideo)|Kontinuierliche und diskrete Spektren]] ⇒ "Continuous and discrete spectra". | ||
| − | * | + | *You can use the following formulas to solve this task: |
| − | :$$\int {t \cdot \cos \left( {\omega _0 t} \right)\ {\rm d}t = \frac{{\cos \left( {\omega _0 t} \right)}}{\omega _0 ^2 }} + \frac{{t \cdot \sin \left( {\omega _0 t} \right)}}{\omega _0 } | + | :$$\sin ^2 \left( \alpha \right) = {1}/{2} \cdot \left( {1 - \cos \left( {2\alpha } \right)} \right),$$ |
| + | :$$\int {t \cdot \cos \left( {\omega _0 t} \right)\ {\rm d}t = \frac{{\cos \left( {\omega _0 t} \right)}}{\omega _0 ^2 }} + \frac{{t \cdot \sin \left( {\omega _0 t} \right)}}{\omega _0 }.$$ | ||
| − | + | ===Questions=== | |
| − | === | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Calculate the spectral function ${X(f)}$. What spectral value results at the frequency $f = 500 \,\text{Hz}$? |
|type="{}"} | |type="{}"} | ||
$X(f = 500 \,\text{Hz}) \ = \ $ { 0.405 3% } $\text{mV/Hz}$ | $X(f = 500 \,\text{Hz}) \ = \ $ { 0.405 3% } $\text{mV/Hz}$ | ||
| − | { | + | {Give the spectral function ${X(f)}$ using the "slitting function" $\text{si}(x) = \sin(x)/x$. What value results for $f = 0$? |
|type="{}"} | |type="{}"} | ||
$X(f = 0) \ = \ $ { 1 3% } $\text{mV/Hz}$ | $X(f = 0) \ = \ $ { 1 3% } $\text{mV/Hz}$ | ||
| − | { | + | {At what frequency $f = f_0$ does the spectrum ${X(f)}$ have the first zero? |
|type="{}"} | |type="{}"} | ||
$f_0 \ = \ $ { 1 3% } $\text{kHz}$ | $f_0 \ = \ $ { 1 3% } $\text{kHz}$ | ||
| − | { | + | {Which of the two statements is true? |
|type="[]"} | |type="[]"} | ||
| − | + | + | + At all multiples of $f_0$ the spectrum has zeros. |
| − | - | + | - At the frequency $f = 1.5 \cdot f_0$ the spectral function is negative. |
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' We use the abbreviation $\omega = 2\pi f$. Then taking advantage of the above symmetry properties: |
:$$X(f) = 2A \cdot \int_0^T {\left( {1 -{t}/{T}} \right)} \cdot \cos \left( {\omega t} \right)\hspace{0.1cm}{\rm d}t.$$ | :$$X(f) = 2A \cdot \int_0^T {\left( {1 -{t}/{T}} \right)} \cdot \cos \left( {\omega t} \right)\hspace{0.1cm}{\rm d}t.$$ | ||
| − | * | + | *This integral is composed of two parts: |
:$$X_1 (f) = 2A \cdot \int_0^T {\cos } \left( {\omega t} \right)\hspace{0.1cm}{\rm d}t = \frac{2A}{\omega } \cdot \sin \left( {\omega T} \right),$$ | :$$X_1 (f) = 2A \cdot \int_0^T {\cos } \left( {\omega t} \right)\hspace{0.1cm}{\rm d}t = \frac{2A}{\omega } \cdot \sin \left( {\omega T} \right),$$ | ||
:$$X_2 (f) = - \frac{2A}{T} \cdot \int_0^T {t \cdot \cos } \left( {\omega t} \right)\hspace{0.1cm}{\rm d}t = - \frac{2A}{T} \cdot \left. {\left[ {\frac{{\cos \left( {\omega t} \right)}}{\omega ^2 } + \frac{{t \cdot \sin \left( {\omega t} \right)}}{\omega }} \right]} \right|_0^T .$$ | :$$X_2 (f) = - \frac{2A}{T} \cdot \int_0^T {t \cdot \cos } \left( {\omega t} \right)\hspace{0.1cm}{\rm d}t = - \frac{2A}{T} \cdot \left. {\left[ {\frac{{\cos \left( {\omega t} \right)}}{\omega ^2 } + \frac{{t \cdot \sin \left( {\omega t} \right)}}{\omega }} \right]} \right|_0^T .$$ | ||
| − | * | + | *Taking into account the upper and lower limits, one obtains: |
:$$X_2 \left( f \right) = - \frac{2A}{T} \cdot \left[ {\frac{{\cos \left( {\omega T} \right)}}{\omega ^2 } - \frac{1}{\omega ^2 } + \frac{{T \cdot \sin \left( {\omega T} \right)}}{\omega }} \right].$$ | :$$X_2 \left( f \right) = - \frac{2A}{T} \cdot \left[ {\frac{{\cos \left( {\omega T} \right)}}{\omega ^2 } - \frac{1}{\omega ^2 } + \frac{{T \cdot \sin \left( {\omega T} \right)}}{\omega }} \right].$$ | ||
| − | * | + | *Adding the two parts, we get: |
:$$X(f) = \frac{2A}{\omega ^2 \cdot T}\cdot \big[ {1 - \cos \left( {\omega T} \right)} \big] = \frac{A}{2\pi ^2 f^2 T} \cdot \big[ {1 - \cos \left( {2\pi fT} \right)} \big].$$ | :$$X(f) = \frac{2A}{\omega ^2 \cdot T}\cdot \big[ {1 - \cos \left( {\omega T} \right)} \big] = \frac{A}{2\pi ^2 f^2 T} \cdot \big[ {1 - \cos \left( {2\pi fT} \right)} \big].$$ | ||
| − | * | + | *At frequency $f = 1/(2T) = 500 \,\text{Hz}$ the argument of the cosine function is equal to $\pi$ and the cosine function itself is equal to $-1$. It follows: |
:$$X( {f ={1}/{2T} = 500\;{\rm Hz}} ) = \frac{4}{\pi^2} \cdot A \cdot T = \frac{4}{\pi^2} \cdot 1\;{\rm V} \cdot 10^{ - 3}\;{\rm s}\hspace{0.15 cm}\underline{= 0.405 \,{\rm mV/Hz}}.$$ | :$$X( {f ={1}/{2T} = 500\;{\rm Hz}} ) = \frac{4}{\pi^2} \cdot A \cdot T = \frac{4}{\pi^2} \cdot 1\;{\rm V} \cdot 10^{ - 3}\;{\rm s}\hspace{0.15 cm}\underline{= 0.405 \,{\rm mV/Hz}}.$$ | ||
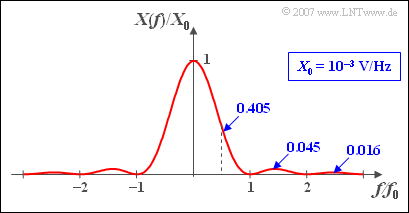
| − | '''(2)''' | + | '''(2)''' With the trigonometric transformation ${1}/{2} \cdot (1 - \cos (2 \alpha)) = \sin^2(\alpha)$ one obtains for the spectral function: |
| − | [[File:P_ID497__Sig_Z_3_1_d_neu.png|right|frame|$ | + | [[File:P_ID497__Sig_Z_3_1_d_neu.png|right|frame|Normalized spectrum $X(f)$]] |
:$$X(f) = A \cdot T \cdot \frac{\sin^2(\pi f T)}{\pi^2 \cdot {f^2 \cdot T^2}} = A \cdot T \cdot {{{\rm si}^2(\pi f T)}}.$$ | :$$X(f) = A \cdot T \cdot \frac{\sin^2(\pi f T)}{\pi^2 \cdot {f^2 \cdot T^2}} = A \cdot T \cdot {{{\rm si}^2(\pi f T)}}.$$ | ||
| − | * | + | *At the frequency $f = 0$ the $\rm si$-function is equal to $1$. From this follows: |
:$$X( {f = 0} ) = A \cdot T \hspace{0.15 cm}\underline{= 1\,{\rm mV/Hz}}.$$ | :$$X( {f = 0} ) = A \cdot T \hspace{0.15 cm}\underline{= 1\,{\rm mV/Hz}}.$$ | ||
| − | + | '''(3)''' The first zero occurs when the argument of the $\rm si$-function is equal to $\pi$. | |
| − | '''(3)''' | + | *From this follows: $f_0 \cdot T = 1$ bzw. $f_0 = 1/T \hspace{0.15 cm}\underline{= 1 \ \text{kHz}}$. |
| − | * | ||
| − | '''(4)''' | + | '''(4)''' The <u>first statement</u> is correct: |
| − | * | + | *The spectrum ${X(f)}$ is equal to ${\rm si}^2(n \cdot \pi) = 0$ at multiples of $f_0$ $(f = n \cdot f_0)$. |
| − | * | + | *The second statement is false: At no frequency $f$ holds: ${X(f)} < 0$ (see sketch). |
{{ML-Fuß}} | {{ML-Fuß}} | ||
| Line 92: | Line 92: | ||
__NOEDITSECTION__ | __NOEDITSECTION__ | ||
| − | [[Category: | + | [[Category:Signal Representation: Exercises|^3.1 Fourier Transform and Its Inverse^]] |
Latest revision as of 14:39, 21 April 2021
A triangular pulse ${x(t)}$ is considered, which is described in the range $–T ≤ t ≤ T$ by the following equation:
- $$x(t) = A \cdot \left( {1 - {\left| \hspace{0.05cm}t \hspace{0.05cm}\right|}/{T}} \right).$$
Let the pulse amplitude be $A = 1\, \text{V}$ and the time parameter $T = 1 \text{ ms}$. For all times $|\hspace{0.05cm} t \hspace{0.05cm} | > T$ ⇒ ${x(t)} = 0$.
To calculate the spectral function ${X(f)}$ you can exploit the following properties:
- The time function is even and thus the spectral function is real:
- $$X\left( f \right) = \int_{ - \infty }^{ + \infty } {x(t)} \cdot {\rm e}^{{\rm j}2\pi ft} {\rm d}t = 2 \cdot \int_0^{ \infty } {x(t)} \cdot \cos \left( {2\pi ft} \right)\ {\rm d}t.$$
- For $|\hspace{0.05cm} t \hspace{0.05cm} | > T$ ⇒ ${x(t)}$ has no components:
- $$X\left( f \right) = 2 \cdot \int_0^T {x(t)} \cdot \cos \left( {2\pi ft} \right)\ {\rm d}t.$$
Hints:
- This exercise belongs to the chapter Fourier Transform and its Inverse.
- Further information on this topic can be found in the (German language) learning video Kontinuierliche und diskrete Spektren ⇒ "Continuous and discrete spectra".
- You can use the following formulas to solve this task:
- $$\sin ^2 \left( \alpha \right) = {1}/{2} \cdot \left( {1 - \cos \left( {2\alpha } \right)} \right),$$
- $$\int {t \cdot \cos \left( {\omega _0 t} \right)\ {\rm d}t = \frac{{\cos \left( {\omega _0 t} \right)}}{\omega _0 ^2 }} + \frac{{t \cdot \sin \left( {\omega _0 t} \right)}}{\omega _0 }.$$
Questions
Solution
(1) We use the abbreviation $\omega = 2\pi f$. Then taking advantage of the above symmetry properties:
- $$X(f) = 2A \cdot \int_0^T {\left( {1 -{t}/{T}} \right)} \cdot \cos \left( {\omega t} \right)\hspace{0.1cm}{\rm d}t.$$
- This integral is composed of two parts:
- $$X_1 (f) = 2A \cdot \int_0^T {\cos } \left( {\omega t} \right)\hspace{0.1cm}{\rm d}t = \frac{2A}{\omega } \cdot \sin \left( {\omega T} \right),$$
- $$X_2 (f) = - \frac{2A}{T} \cdot \int_0^T {t \cdot \cos } \left( {\omega t} \right)\hspace{0.1cm}{\rm d}t = - \frac{2A}{T} \cdot \left. {\left[ {\frac{{\cos \left( {\omega t} \right)}}{\omega ^2 } + \frac{{t \cdot \sin \left( {\omega t} \right)}}{\omega }} \right]} \right|_0^T .$$
- Taking into account the upper and lower limits, one obtains:
- $$X_2 \left( f \right) = - \frac{2A}{T} \cdot \left[ {\frac{{\cos \left( {\omega T} \right)}}{\omega ^2 } - \frac{1}{\omega ^2 } + \frac{{T \cdot \sin \left( {\omega T} \right)}}{\omega }} \right].$$
- Adding the two parts, we get:
- $$X(f) = \frac{2A}{\omega ^2 \cdot T}\cdot \big[ {1 - \cos \left( {\omega T} \right)} \big] = \frac{A}{2\pi ^2 f^2 T} \cdot \big[ {1 - \cos \left( {2\pi fT} \right)} \big].$$
- At frequency $f = 1/(2T) = 500 \,\text{Hz}$ the argument of the cosine function is equal to $\pi$ and the cosine function itself is equal to $-1$. It follows:
- $$X( {f ={1}/{2T} = 500\;{\rm Hz}} ) = \frac{4}{\pi^2} \cdot A \cdot T = \frac{4}{\pi^2} \cdot 1\;{\rm V} \cdot 10^{ - 3}\;{\rm s}\hspace{0.15 cm}\underline{= 0.405 \,{\rm mV/Hz}}.$$
(2) With the trigonometric transformation ${1}/{2} \cdot (1 - \cos (2 \alpha)) = \sin^2(\alpha)$ one obtains for the spectral function:
- $$X(f) = A \cdot T \cdot \frac{\sin^2(\pi f T)}{\pi^2 \cdot {f^2 \cdot T^2}} = A \cdot T \cdot {{{\rm si}^2(\pi f T)}}.$$
- At the frequency $f = 0$ the $\rm si$-function is equal to $1$. From this follows:
- $$X( {f = 0} ) = A \cdot T \hspace{0.15 cm}\underline{= 1\,{\rm mV/Hz}}.$$
(3) The first zero occurs when the argument of the $\rm si$-function is equal to $\pi$.
- From this follows: $f_0 \cdot T = 1$ bzw. $f_0 = 1/T \hspace{0.15 cm}\underline{= 1 \ \text{kHz}}$.
(4) The first statement is correct:
- The spectrum ${X(f)}$ is equal to ${\rm si}^2(n \cdot \pi) = 0$ at multiples of $f_0$ $(f = n \cdot f_0)$.
- The second statement is false: At no frequency $f$ holds: ${X(f)} < 0$ (see sketch).