Difference between revisions of "Aufgaben:Exercise 3.2: From the Spectrum to the Signal"
From LNTwww
| Line 57: | Line 57: | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
'''(1)''' Correct is the <u>proposed solution 2</u> ⇒ $x(t)$ is <u>purely real</u>: | '''(1)''' Correct is the <u>proposed solution 2</u> ⇒ $x(t)$ is <u>purely real</u>: | ||
| − | *For the imaginary signal component ⇒ $x_{\rm I}(t)$ the integrand is an odd function (even numerator, odd denominator) | + | *For the imaginary signal component ⇒ $x_{\rm I}(t)$ the integrand is an odd function (even numerator, odd denominator). |
*Thus the integral from $-\infty$ bis $+\infty$ is zero. | *Thus the integral from $-\infty$ bis $+\infty$ is zero. | ||
| − | *In contrast, for the real component $x_{\rm R}(t)$ ⇒ even integrand (odd numerator, odd denominator) yields a non-zero value. | + | *In contrast, for the real component $x_{\rm R}(t)$ ⇒ even integrand (odd numerator, odd denominator) yields a non-zero value. |
'''(2)''' With the abbreviation $a = 2\pi t$ can be written for the time signal: | '''(2)''' With the abbreviation $a = 2\pi t$ can be written for the time signal: | ||
| − | |||
:$$x(t) = x_{\rm R} \left( t \right) = \frac{{4\,{\rm V}}}{\pi }\int_0^\infty {\frac{{\sin( {af} )}}{f}}\hspace{0.1cm} {\rm d}f.$$ | :$$x(t) = x_{\rm R} \left( t \right) = \frac{{4\,{\rm V}}}{\pi }\int_0^\infty {\frac{{\sin( {af} )}}{f}}\hspace{0.1cm} {\rm d}f.$$ | ||
| Line 78: | Line 77: | ||
| − | '''(3)''' | + | '''(3)''' $x(t)$ has a jumping point at $t = 0$. The right-hand limit value for $t \rightarrow 0$ is $x_+ = +2\,\text{V}$. |
| − | *If one approaches the | + | *If one approaches the jumping point of negative times as close as desired, one obtains $x_– = -\hspace{-0.05cm}2\,\text{V}$. |
| + | *The following then applies to the actual signal value at $t = 0$: | ||
:$$x( {t = 0} ) = {1}/{2}\cdot ( x_{+} + x_{-} ) \hspace{0.15 cm}\underline{= 0}.$$ | :$$x( {t = 0} ) = {1}/{2}\cdot ( x_{+} + x_{-} ) \hspace{0.15 cm}\underline{= 0}.$$ | ||
| Line 93: | Line 93: | ||
Here is a second solution: | Here is a second solution: | ||
| − | *The right | + | *The right–hand limit for $f → 0$ is $X_+ = -\text{j} \cdot \infty$,– and the left–hand limit $X_- = \text{j} \cdot \infty$. |
| − | *So the relationship also applies with regard to the spectral value at $f = 0$ | + | *So the relationship also applies with regard to the spectral value at $f = 0$: |
:$$X( {f = 0}) = {1}/{2}\cdot \left( {X_{ +} + X_{-} } \right) = 0.$$ | :$$X( {f = 0}) = {1}/{2}\cdot \left( {X_{ +} + X_{-} } \right) = 0.$$ | ||
Latest revision as of 15:25, 21 April 2021
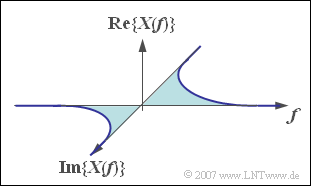
Given the spectral function
- $$X(f) = \frac{{2\,{\rm V}}}{ { {\rm j}\pi f}}.$$
The associated time function $x(t)$ can be determined with the help of The second Fourier integral :
- $$x(t) = \int_{ - \infty }^{ + \infty } {X(f)} \cdot {\rm e}^{{\rm j}2\pi ft} {\rm d} f = x_{\rm R} (t) + {\rm j} \cdot x_{\rm I} (t),$$
where holds for the real part and the imaginary part, respectively:
- $$x_{\rm R} (t) = 2\,{\rm V} \cdot \int_{ - \infty }^{ + \infty } {\frac{{\sin ( {2\pi ft} )}}{ {\pi f}}}\hspace{0.1cm} {\rm d}f, $$
- $$x_{\rm I} (t) = -2\, {\rm V} \cdot \int_{ - \infty }^{ + \infty } {\frac{ {\cos ( {2\pi ft} )}}{ {\pi f}}} \hspace{0.1cm}{\rm d}f.$$
Hints:
- This exercise belongs to the chapter Fourier Transform and its Inverse.
- If necessary, use the following information for the solution:
- $$x( {t = 0}) = \int_{ - \infty }^{ + \infty } {X( f )}\hspace{0.1cm} {\rm d}f,\hspace{0.5cm} X( {f = 0} ) = \int_{ - \infty }^{ + \infty } {x( t)}\hspace{0.1cm} {\rm d}t ,\hspace{0.5cm}\int_0^\infty {\frac{{\sin ( {ax} )}}{x}}\hspace{0.1cm} {\rm d}x = {\rm sign} ( a ) \cdot{\pi }/{2}. $$
Questions
Solution
(1) Correct is the proposed solution 2 ⇒ $x(t)$ is purely real:
- For the imaginary signal component ⇒ $x_{\rm I}(t)$ the integrand is an odd function (even numerator, odd denominator).
- Thus the integral from $-\infty$ bis $+\infty$ is zero.
- In contrast, for the real component $x_{\rm R}(t)$ ⇒ even integrand (odd numerator, odd denominator) yields a non-zero value.
(2) With the abbreviation $a = 2\pi t$ can be written for the time signal:
- $$x(t) = x_{\rm R} \left( t \right) = \frac{{4\,{\rm V}}}{\pi }\int_0^\infty {\frac{{\sin( {af} )}}{f}}\hspace{0.1cm} {\rm d}f.$$
This leads to the result using the given definite integral:
- $$x(t) = \frac{{4\,{\rm V}}}{\pi } \cdot \frac{\pi }{2} \cdot {\mathop{\rm sign}\nolimits} ( t ) = 2\;{\rm V} \cdot {\mathop{\rm sign}\nolimits} ( t ).$$
- For $t > 0$ $x(t) = +2\,\text{V}$ .
- Correspondingly, $x(t) = -\hspace{-0.1cm}2\,\text{V}$ applies for $t < 0$.
- The signal $x(t)$ thus describes a step function from $-\hspace{-0.05cm}2\,\text{V}$ auf $+2\,\text{V}$.
(3) $x(t)$ has a jumping point at $t = 0$. The right-hand limit value for $t \rightarrow 0$ is $x_+ = +2\,\text{V}$.
- If one approaches the jumping point of negative times as close as desired, one obtains $x_– = -\hspace{-0.05cm}2\,\text{V}$.
- The following then applies to the actual signal value at $t = 0$:
- $$x( {t = 0} ) = {1}/{2}\cdot ( x_{+} + x_{-} ) \hspace{0.15 cm}\underline{= 0}.$$
- The same result is obtained by considering the relation
- $$x( t = 0) = \int_{ - \infty }^{ + \infty } {X( f)}\hspace{0.1cm} {\rm d}f = 0.$$
(4) The spectral value at $f = 0$ is equal to the integral from $-\infty$ to $+\infty$ over the time function $x(t)$:
- $$X( f = 0) = \int_{ - \infty }^{ + \infty } {x( t)}\hspace{0.1cm} {\rm d}t \hspace{0.15 cm}\underline{= 0}.$$
Here is a second solution:
- The right–hand limit for $f → 0$ is $X_+ = -\text{j} \cdot \infty$,– and the left–hand limit $X_- = \text{j} \cdot \infty$.
- So the relationship also applies with regard to the spectral value at $f = 0$:
- $$X( {f = 0}) = {1}/{2}\cdot \left( {X_{ +} + X_{-} } \right) = 0.$$