Difference between revisions of "Aufgaben:Exercise 3.6: Even and Odd Time Signals"
| Line 57: | Line 57: | ||
:$$U( {f = 0.5\;{\rm{kHz}}} ) = - {\rm{j}} \cdot \frac{ {A_u \cdot T}}{ {\rm{\pi }}} \cdot {\mathop{\rm si}\nolimits} ( {{ {\rm{\pi }}}/{2}} ) = - {\rm{j}} \cdot \frac{2}{ { {\rm{\pi }}^{\rm{2}} }} \cdot A_{\rm u} \cdot T.$$ | :$$U( {f = 0.5\;{\rm{kHz}}} ) = - {\rm{j}} \cdot \frac{ {A_u \cdot T}}{ {\rm{\pi }}} \cdot {\mathop{\rm si}\nolimits} ( {{ {\rm{\pi }}}/{2}} ) = - {\rm{j}} \cdot \frac{2}{ { {\rm{\pi }}^{\rm{2}} }} \cdot A_{\rm u} \cdot T.$$ | ||
| − | *The imaginary part is | + | *The imaginary part is ${\rm Im}[U(f=0.5 \,\text{kHz})]\; \underline{\approx 0.2 \,\text{mV/Hz}}$. |
| − | *In contrast, the si function at $f \cdot T = 1$ yields the value zero, while the cosine is equal to $-1$ | + | *In contrast, the $\rm si$–function at $f \cdot T = 1$ yields the value zero, while the cosine is equal to $-1$. Thus with $A_u = 1\,\text{V}$ and $T = 1\,\text{ms}$ one obtains: |
:$$U( {f = 1\;{\rm{kHz}}} ) = {\rm{j}} \cdot \frac{ {A_{\rm u} \cdot T}}{ { {\rm{2\pi }}}} \hspace{0.3 cm} \Rightarrow \hspace{0.3 cm} {\rm Re} [\text{...}] \hspace{0.15 cm}\underline{ = 0}, \hspace{0.3 cm}{\rm Im} [\text{...}] \hspace{0.15 cm}\underline{\approx 0.159 \;{\rm{mV/Hz}}}.$$ | :$$U( {f = 1\;{\rm{kHz}}} ) = {\rm{j}} \cdot \frac{ {A_{\rm u} \cdot T}}{ { {\rm{2\pi }}}} \hspace{0.3 cm} \Rightarrow \hspace{0.3 cm} {\rm Re} [\text{...}] \hspace{0.15 cm}\underline{ = 0}, \hspace{0.3 cm}{\rm Im} [\text{...}] \hspace{0.15 cm}\underline{\approx 0.159 \;{\rm{mV/Hz}}}.$$ | ||
| Line 64: | Line 64: | ||
| − | '''(2)''' According to the | + | '''(2)''' According to the "Assignment Theorem", an odd time function $u(t)$ always has an imaginary and at the same time odd spectrum $U( { - f} ) = - U( f )$. With the boundary transition $f \rightarrow \infty$ follows from the given equation |
| − | $U( { - f} ) = - U( f ). | ||
:$$U( f ) = - {\rm{j}} \cdot \frac{ {A_u \cdot T}}{ {2{\rm{\pi }}fT}}\big[ { {\mathop{\rm si}\nolimits} ( {{\rm{\pi }}fT} ) - \cos ( { {\rm{\pi }}fT} )} \big]$$ | :$$U( f ) = - {\rm{j}} \cdot \frac{ {A_u \cdot T}}{ {2{\rm{\pi }}fT}}\big[ { {\mathop{\rm si}\nolimits} ( {{\rm{\pi }}fT} ) - \cos ( { {\rm{\pi }}fT} )} \big]$$ | ||
| − | the result $U(f = 0) = 0$. Formally, one could confirm this result by applying l'Hospital's rule. | + | the result $U(f = 0) = 0$. Formally, one could confirm this result by applying l'Hospital's rule. |
We proceed a little more pragmatically. | We proceed a little more pragmatically. | ||
| Line 77: | Line 76: | ||
*For even smaller frequency values, the result also becomes smaller and smaller. | *For even smaller frequency values, the result also becomes smaller and smaller. | ||
| − | *You get to the result $U(f = 0)\;\underline{ = 0}$ | + | *You get to the result $U(f = 0)\;\underline{ = 0}$ more quickly if you take into account that the integral over $u(t)$ disappears. |
*So you don't have to calculate at all. | *So you don't have to calculate at all. | ||
| − | '''(3)''' The signal $x(t)$ can be divided into | + | '''(3)''' The signal $x(t)$ can be divided into an even and an odd part, which lead to the even real part and the odd imaginary part of $X(f)$ : |
| − | *The even part is equal to the function $g(t)$ with $A_g = 3\,\text{V}$. From this follows for the real part of the spectral value at $f \cdot T = 0.5$: | + | *The even part is equal to the function $g(t)$ with $A_g = 3\,\text{V}$. From this follows for the real part of the spectral value at $f \cdot T = 0.5$: |
:$${\mathop{\rm Re}\nolimits} \left[ {X( {f \cdot T = 0.5} )} \right] = A_{\rm g} \cdot T \cdot {\mathop{\rm si}\nolimits} ( {{ {\rm{\pi }}}/{2}} ) \hspace{0.15 cm}\underline{= 1.91 \;{\rm{mV/Hz}}}{\rm{.}}$$ | :$${\mathop{\rm Re}\nolimits} \left[ {X( {f \cdot T = 0.5} )} \right] = A_{\rm g} \cdot T \cdot {\mathop{\rm si}\nolimits} ( {{ {\rm{\pi }}}/{2}} ) \hspace{0.15 cm}\underline{= 1.91 \;{\rm{mV/Hz}}}{\rm{.}}$$ | ||
| − | *The imaginary part results from the spectral function $U(f)$ with $A_u = 1\,\text{V}$. This was already calculated in subtask '''(1)''' | + | *The imaginary part results from the spectral function $U(f)$ with $A_u = 1\,\text{V}$. This was already calculated in subtask '''(1)''': |
:$${\mathop{\rm Im}\nolimits} \left[ {X( {f \cdot T = 0.5} )} \right] \hspace{0.15 cm}\underline{\approx - 0.2 \;{\rm{mV/Hz}}}{\rm{.}}$$ | :$${\mathop{\rm Im}\nolimits} \left[ {X( {f \cdot T = 0.5} )} \right] \hspace{0.15 cm}\underline{\approx - 0.2 \;{\rm{mV/Hz}}}{\rm{.}}$$ | ||
Latest revision as of 14:22, 27 April 2021
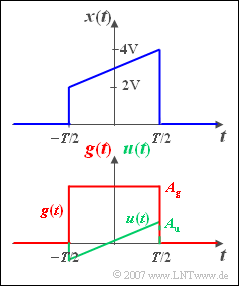
We are looking for the spectrum $X(f)$ of the pulse $x(t)$ sketched opposite, which rises linearly from $2\hspace{0.05cm} \text{V}$ to $4\hspace{0.05cm} \text{V}$ in the range from $–T/2$ to $+T/2$ and is zero outside.
The spectral functions of the signals $g(t)$ and $u(t)$ shown below are assumed to be known:
- The even (German: gerade) rectangular time function $g(t)$ has the spectrum
- $$G( f ) = A_g \cdot T \cdot {\mathop{\rm si}\nolimits}( { {\rm{\pi }}fT} ) \hspace{0.3cm} {\rm{with}}\hspace{0.3cm} {\mathop{\rm si}\nolimits}( x ) = {\sin ( x )}/{x}.$$
- The spectrum of the odd (German: ungerade) function $u(t)$ is:
- $$U( f ) = - {\rm{j}} \cdot \frac{ {A_u \cdot T}}{ {2{\rm{\pi }}fT}}\big[ {{\mathop{\rm si}\nolimits} ( { {\rm{\pi }}fT} ) - \cos ( { {\rm{\pi }}fT} )} \big].$$
Hints:
- This exercise belongs to the chapter Fourier Transform Theorems.
- All the theorems presented here are illustrated with examples in the (German language) learning video
Gesetzmäßigkeiten der Fouriertransformation ⇒ "Regularities to the Fourier transform". - Solve this task with the help of the Assignment Theorem.
- For the first two subtasks use the signal parameters $A_u = 1\,\text{V}$ and $T = 1\,\text{ms}$.
Questions
Solution
- $$U( {f = 0.5\;{\rm{kHz}}} ) = - {\rm{j}} \cdot \frac{ {A_u \cdot T}}{ {\rm{\pi }}} \cdot {\mathop{\rm si}\nolimits} ( {{ {\rm{\pi }}}/{2}} ) = - {\rm{j}} \cdot \frac{2}{ { {\rm{\pi }}^{\rm{2}} }} \cdot A_{\rm u} \cdot T.$$
- The imaginary part is ${\rm Im}[U(f=0.5 \,\text{kHz})]\; \underline{\approx 0.2 \,\text{mV/Hz}}$.
- In contrast, the $\rm si$–function at $f \cdot T = 1$ yields the value zero, while the cosine is equal to $-1$. Thus with $A_u = 1\,\text{V}$ and $T = 1\,\text{ms}$ one obtains:
- $$U( {f = 1\;{\rm{kHz}}} ) = {\rm{j}} \cdot \frac{ {A_{\rm u} \cdot T}}{ { {\rm{2\pi }}}} \hspace{0.3 cm} \Rightarrow \hspace{0.3 cm} {\rm Re} [\text{...}] \hspace{0.15 cm}\underline{ = 0}, \hspace{0.3 cm}{\rm Im} [\text{...}] \hspace{0.15 cm}\underline{\approx 0.159 \;{\rm{mV/Hz}}}.$$
(2) According to the "Assignment Theorem", an odd time function $u(t)$ always has an imaginary and at the same time odd spectrum $U( { - f} ) = - U( f )$. With the boundary transition $f \rightarrow \infty$ follows from the given equation
- $$U( f ) = - {\rm{j}} \cdot \frac{ {A_u \cdot T}}{ {2{\rm{\pi }}fT}}\big[ { {\mathop{\rm si}\nolimits} ( {{\rm{\pi }}fT} ) - \cos ( { {\rm{\pi }}fT} )} \big]$$
the result $U(f = 0) = 0$. Formally, one could confirm this result by applying l'Hospital's rule.
We proceed a little more pragmatically.
- For example, if we set $f \cdot T = 0.01$, we obtain:
$$U( {f \cdot T = 0.01}) = -{\rm{j}} \cdot \frac{ {A_{\rm u} \cdot T}}{{0.02{\rm{\pi }}}}\big[ {{\mathop{\rm si}\nolimits} ( {0.01{\rm{\pi }}} ) - \cos ( {0.01{\rm{\pi }}} )} \big ] = - {\rm{j}} \cdot \frac{ {A{\rm u} \cdot T}}{{0.02{\rm{\pi }}}}( {0.999836 - 0.999507} ) \approx - {\rm{j}} \cdot 5 \cdot 10^{ - 6} \;{\rm{V/Hz}}{\rm{.}}$$
- For even smaller frequency values, the result also becomes smaller and smaller.
- You get to the result $U(f = 0)\;\underline{ = 0}$ more quickly if you take into account that the integral over $u(t)$ disappears.
- So you don't have to calculate at all.
(3) The signal $x(t)$ can be divided into an even and an odd part, which lead to the even real part and the odd imaginary part of $X(f)$ :
- The even part is equal to the function $g(t)$ with $A_g = 3\,\text{V}$. From this follows for the real part of the spectral value at $f \cdot T = 0.5$:
- $${\mathop{\rm Re}\nolimits} \left[ {X( {f \cdot T = 0.5} )} \right] = A_{\rm g} \cdot T \cdot {\mathop{\rm si}\nolimits} ( {{ {\rm{\pi }}}/{2}} ) \hspace{0.15 cm}\underline{= 1.91 \;{\rm{mV/Hz}}}{\rm{.}}$$
- The imaginary part results from the spectral function $U(f)$ with $A_u = 1\,\text{V}$. This was already calculated in subtask (1):
- $${\mathop{\rm Im}\nolimits} \left[ {X( {f \cdot T = 0.5} )} \right] \hspace{0.15 cm}\underline{\approx - 0.2 \;{\rm{mV/Hz}}}{\rm{.}}$$