Aufgaben:Exercise 4.3: Pointer Diagram Representation

• Return to book

Pointer diagram of a harmonic

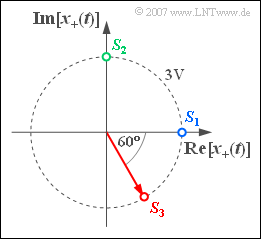
We consider an analytical signal  $x_+(t)$, which is defined by the drawn diagram in the complex plane.  Depending on the choice of signal parameters, this results in three physical band-pass signals  $x_1(t)$,  $x_2(t)$  and  $x_3(t)$, which differ by different starting points  $S_i = x_i(t = 0)$.

In addition, the angular velocities of the three constellations  (blue, green and red point)  are also different:

• The (blue) analytical signal  $x_{1+}(t)$  starts at  $S_1 = 3 \ \rm V$.  The angular velocity is  $\omega_1 = \pi \cdot 10^{4} \ 1/\text{s}$.
• The signal  $x_{2+}(t)$  starts at the green starting point  $S_2 = {\rm j} \cdot 3 \ \text{V}$  and, compared to  $x_{1+}(t)$ , rotates with twice the angular velocity  ⇒   $\omega_2 = 2 \cdot \omega_1$.
• The signal $x_{3+}(t)$ starts at the red starting point  $S_3 = 3 \ \text{V} \cdot \text{e}^{–\text{j}\hspace{0.05cm}\cdot\hspace{0.05cm}\pi /3}$  and rotates with same speed as the signal  $x_{2+}(t)$.

Hints:

• This exercise belongs to the chapter  Analytical Signal and its Spectral Function.
• The interactive applet  Physical signal & Analytical Signal  illustrates the topic covered here.

Questions

1

What are the amplitudes of all signals considered??

$A\ = \ $  $\text{V}$

2

What are the frequency and phase values of the signal  $x_1(t)$?

$f_1\ = \ $  $\text{kHz}$

$\varphi_1\ = \ $  $\text{deg}$

3

What are the frequency and phase values of the signal  $x_2(t)$?

$f_2\ = \ $  $\text{kHz}$

$\varphi_2\ = \ $  $\text{deg}$

4

What are the values of the frequency and phase of the signal   $x_3(t)$?

$f_3\ = \ $  $\text{kHz}$

$\varphi_3\ = \ $  $\text{deg}$

5

After what time  $t_1$  is the analytical signal  $x_{3+}(t)$  equal to the initial value  $x_{3+}(t = 0)$for the first time again?

$t_1\ = \ $  $\text{ms}$

6

After what time  $t_2$  is the physical signal  $x_3(t)$  for the first time again as large as at time  $t = 0$?

$t_2\ = \ $  $\text{ms}$

Solution

Solution

(1)  The amplitude of the harmonic oscillation is equal to the pointer length. For all signals  $A \; \underline{= 3 \ \text{V}}$.

(2)  The sought frequency is given by  $f_1 = \omega_1/(2\pi ) \; \underline{= 5 \ \text{kHz}}$.

• The phase can be determined from  $S_1 = 3 \ \text{V} \cdot \text{e}^{–\text{j} \hspace{0.05cm}\cdot \hspace{0.05cm} \varphi_1}$  and is  $\varphi_1 \; \underline{= 0}$.
• In total this gives

$$x_1(t) = 3\hspace{0.05cm}{\rm V} \cdot {\cos} ( 2 \pi \cdot {\rm 5 \hspace{0.05cm} kHz}\cdot t) .$$

(3)  Because of  $\omega_2 = 2\cdot \omega_1$ , the frequency is now  $f_2 = 2 \cdot f_1 \; \underline{= 10 \ \text{kHz}}$.

• The phase is obtained with the starting time  $S_2$  at  $\text{e}^{–\text{j}\hspace{0.05cm} \cdot \hspace{0.05cm}\varphi_2} = \text{j}$   ⇒   $\varphi_2 \; \underline{= -\pi /2 \; (-90^{\circ})}$.
• Thus the time function is:

$$x_2(t) = 3\hspace{0.05cm}{\rm V} \cdot {\cos} ( 2 \pi \cdot {\rm 10 \hspace{0.05cm} kHz}\cdot t + 90^\circ) = -3\hspace{0.05cm}{\rm V} \cdot {\sin} ( 2 \pi \cdot {\rm 10 \hspace{0.05cm} kHz}\cdot t ).$$

This signal is "minus-sine", which can also be read directly from the pointer diagram:

• The real part of  $x_{2+}(t)$  at time  $t = 0$  is zero. Since the pointer turns counterclockwise, the real part is negative at first.
• After a quarter turn,  $x_2(T/4) = - 3 \ \text{V}$.
• If one continues to turn counterclockwise in steps of  $90^\circ$  , the signal values  $0 \ \text{V}$,  $3 \ \text{V}$  and  $0 \ \text{V}$ result.

(4)  This sub-task can be solved analogously to questions  (2)  and (3) :  

$$f_3 \; \underline{= 10 \ \text{kHz}}, \ \varphi_3 \; \underline{= 60^\circ}.$$

(5)  The pointer requires exactly the period  $T_3 = 1/f_3 \; \underline{= 0.1 \ \text{ms}} \;(= t_1)$ for one revolution..

(6)  The analytical signal starts at  $S_3 = 3 \ \text{V} \cdot \text{e}^{–\text{j}\hspace{0.05cm} \cdot \hspace{0.05cm}60^{\circ}}$.

• If the signal rotates further by  $120^\circ$ , exactly the same real part results.
• The following relationship then applies with  $t_2 = t_1/3 \; \underline{= 0.033 \ \text{ms}} $ :

$$x_3(t = t_2) = x_3(t = 0) = 3\hspace{0.05cm}{\rm V} \cdot {\cos} ( 60^\circ) = 1.5\hspace{0.05cm}{\rm V} .$$