Difference between revisions of "Aufgaben:Exercise 5.3: Mean Square Error"
| Line 10: | Line 10: | ||
:$$x_1(t) = A \cdot {\rm e}^{- \pi (t/T)^2} \hspace{0.05cm},$$ | :$$x_1(t) = A \cdot {\rm e}^{- \pi (t/T)^2} \hspace{0.05cm},$$ | ||
| − | *a [[Signal_Representation/ | + | *a [[Signal_Representation/Special_Cases_of_Pulses#Rectangular_pulse|rectangular pulse]] $x_2(t)$ with amplitude $A$ and (equivalent) duration $T$: |
:$$x_2(t) = \left\{ \begin{array}{c} A \\ | :$$x_2(t) = \left\{ \begin{array}{c} A \\ | ||
Revision as of 16:01, 17 May 2021
We consider three pulses, namely
- a Gaussian pulse with amplitude $A$ and equivalent duration $T$:
- $$x_1(t) = A \cdot {\rm e}^{- \pi (t/T)^2} \hspace{0.05cm},$$
- a rectangular pulse $x_2(t)$ with amplitude $A$ and (equivalent) duration $T$:
- $$x_2(t) = \left\{ \begin{array}{c} A \\ 0 \\ \end{array} \right.\quad \begin{array}{*{10}c} {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{20}c} |t| < T/2 \hspace{0.05cm}, \\ |t| > T/2 \hspace{0.05cm}, \\ \end{array}$$
- a so called "sinc pulse" according to the following definition:
- $$x_3(t) = A \cdot {\rm sinc}(t/ T) ,\hspace{0.15cm}{\rm sinc}(x) = \sin(\pi x)/(\pi x)\hspace{0.05cm}.$$
Let the signal parameters be $A = 1\ {\rm V}$ and $T = 1\ {\rm ms}$ in each case.
The conventional Fourier transform leads to the following spectral functions:
- $X_1(f)$ is also Gaussian,
- $X_2(f)$ runs according to the $\rm sinc$ function,
- $X_3(f)$ is constant for $|f| < 1/(2 T)$ and outside zero.
For all spectral functions, $X(f = 0) = A \cdot T$.
If the discrete-frequency spectrum is determined by the Discrete Fourier Transform with the DFT parameters
- $N = 512$ ⇒ number of samples considered in the time and frequency domain,
- $f_{\rm A}$ ⇒ interpolation distance in the frequency domain,
this will lead to distortions due to truncation and/or aliasing errors.
The other DFT parameters are clearly fixed withn $N$ and $f_{\rm A}$. The following applies to these:
- $$f_{\rm P} = N \cdot f_{\rm A},\hspace{0.3cm}T_{\rm P} = 1/f_{\rm A},\hspace{0.3cm}T_{\rm A} = T_{\rm P}/N \hspace{0.05cm}.$$
The accuracy of the respective DFT approximation is captured by the "mean square error" $\rm (MSE)$.
Here, we use the designation $\rm MQF$ ⇒ (German: "Mittlerer Quadratischer Fehler"):
- $${\rm MQF} = \frac{1}{N}\cdot \sum_{\mu = 0 }^{N-1} \left|X(\mu \cdot f_{\rm A})-\frac{D(\mu)}{f_{\rm A}}\right|^2 \hspace{0.05cm}.$$
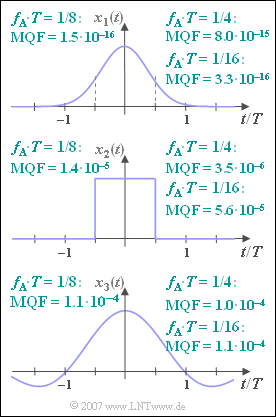
The resulting MQF values are given in the graph above, valid for $N = 512$ as well as for
- $f_{\rm A} \cdot T = 1/4$,
- $f_{\rm A} \cdot T = 1/8$,
- $f_{\rm A} \cdot T = 1/16$.
Hints:
- This task belongs to the chapter Possible errors when using DFT.
- The theory for this chapter is summarised in the (German language) learning video
Fehlermöglichkeiten bei Anwendung der DFT ⇒ "Possible errors when using DFT".
Questions
Solution
- $$f_{\rm P} \cdot T = N \cdot (f_{\rm A} \cdot T) = 64.$$
- This covers the frequency range $–f_{\rm P}/2 \leq f < f_{\rm P}/2$ :
- $$f_{\rm max }\cdot T \hspace{0.15 cm}\underline{= 32}\hspace{0.05cm}.$$
(2) The periodisation of the time function is based on the parameter $T_{\rm P} = 1/f_{\rm A} = 8T$.
- The distance between two samples is therefore
- $$T_{\rm A}/T = \frac{T_{\rm P}/T}{N} = \frac{8}{512}\hspace{0.15 cm}\underline{ = 0.015625}\hspace{0.05cm}.$$
(3) Correct is the proposed solution 1 ⇒ increase of the termination error:
- This measure simultaneously halves $T_{\rm P}$ from $8T$ to $4T$ .*Thus, only samples in the range $–2T \leq t < 2T$, are taken into account, which increases the termination error.
- The mean square error $(\rm MQF)$ increases from $0.15 \cdot 10^{-15}$ to $8 \cdot 10^{-15}$ for the Gaussian pulse $x_1(t)$ , although the aliasing error actually decreases slightly by this measure.
(4) Correct is the proposed solution 2 ⇒ increase of the aliasing error::
- By halving $f_{\rm A}$ wird auch $f_{\rm P}$ is also halved.
- As a result, the aliasing error becomes somewhat larger with a smaller termination error at the same time.
- Overall, for the Gaussian pulse $x_1(t)$ , the mean square error $(\rm MQF)$ increases from $1.5 \cdot 10^{-16}$ to $3.3 \cdot 10^{-16}$.
(5) Proposed solutions 1 and 2 are correct:
- As can be seen from the graph, the last statement is not true in contrast to the first two.
- Due to the slow, $\rm si$–shaped decay of the spectral function, the aliasing error dominates.
- The $\rm MQF$ value at $f_{\rm A} \cdot T = 1/8$ with $1.4 \cdot 10^{-5}$ is therefore significantly larger than for the Gaussian pulse $(1.5 \cdot 10^{-16})$.
(6) Proposed solution 3 is correct:
- The spectral function $X_3(f)$ here has a rectangular lead, so that the first two statements do not apply.
- On the other hand, a termination error is unavoidable with this $\rm si$–shaped time function. This leads to the large $\rm MQF$ values given.