Difference between revisions of "Aufgaben:Exercise 2.2: DC Component of Signals"
From LNTwww
m (Text replacement - "Category:Exercises for Signal Representation" to "Category:Signal Representation: Exercises") |
|||
| (6 intermediate revisions by 2 users not shown) | |||
| Line 3: | Line 3: | ||
}} | }} | ||
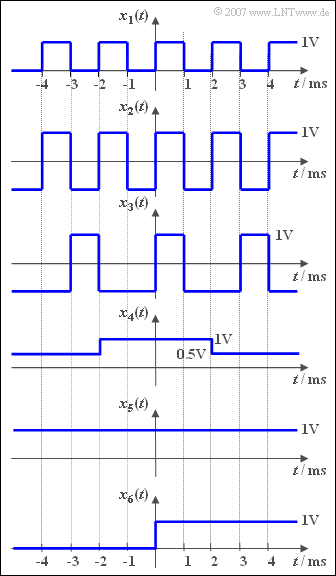
| − | [[File:P_ID273__Sig_A_2_2.png|right|frame| | + | [[File:P_ID273__Sig_A_2_2.png|right|frame|Square wave signal with/ without DC component]] |
| − | The graph shows | + | The graph shows six time signals defined for all times $($from $-\infty$ to $+\infty)$. For all sample signals $x_i(t)$ the associated spectral function can be written as: |
:$$X_i(f)=A_0\cdot{\rm \delta}(f)+\Delta X_i(f).$$ | :$$X_i(f)=A_0\cdot{\rm \delta}(f)+\Delta X_i(f).$$ | ||
| − | Here | + | Here: |
| − | *$A_0$ is the DC component | + | *$A_0$ is the DC component of the signal. |
| − | *$\Delta X_i(f)$ is the spectrum of the residual signal reduced by the DC component $\Delta x_i(t) = x_i(t) - A_0$ | + | *$\Delta X_i(f)$ is the spectrum of the residual signal reduced by the DC component: |
| − | + | :$$\Delta x_i(t) = x_i(t) - A_0.$$ | |
| − | |||
| − | |||
| − | |||
| − | |||
''Hint:'' | ''Hint:'' | ||
| − | *This exercise belongs to the chapter [[Signal_Representation/Direct_Current_Signal_-_Limit_Case_of_a_Periodic_Signal|Direct Current Signal - Limit Case of a Periodic Signal]]. | + | *This exercise belongs to the chapter <br>[[Signal_Representation/Direct_Current_Signal_-_Limit_Case_of_a_Periodic_Signal|Direct Current Signal - Limit Case of a Periodic Signal]]. |
| − | |||
| − | |||
| Line 72: | Line 66: | ||
'''(2)''' Only <u>solution 5 is correct</u>: | '''(2)''' Only <u>solution 5 is correct</u>: | ||
| − | *If the DC component $1\text{V}$ is subtracted from the signal $x_5(t)$ | + | *If the DC component $1\text{V}$ is subtracted from the signal $x_5(t)$, the residual signal $\Delta x_5(t) = x5(t) - 1\text{V}$ is zero. |
*Accordignly, the spectral function is $\Delta X_5(f) = 0$. | *Accordignly, the spectral function is $\Delta X_5(f) = 0$. | ||
| − | *For all other time courses $\Delta x_i(t)$ | + | *For all other time courses $\Delta x_i(t)ßne 0$ and thus the associated spectral function $\Delta X_i(f)\ne 0$, too. |
'''(3)''' Given a periodic signal, averaging over a period duration is sufficient to calculate the DC signal component $A_0$ . | '''(3)''' Given a periodic signal, averaging over a period duration is sufficient to calculate the DC signal component $A_0$ . | ||
| − | *For | + | *For signal $x_3(t)$ the period duration is $T_0 = 3\,\text{ms}$. This results in the required DC component:$$A_0=\rm \frac{1}{3\,ms}\cdot \big[1\,V\cdot 1\,ms+(-1\,V)\cdot 2\,ms \big] |
\hspace{0.15cm}\underline{=-0.333\,V}.$$ | \hspace{0.15cm}\underline{=-0.333\,V}.$$ | ||
| Line 85: | Line 79: | ||
'''(4)''' The signal $x_4(t)$ can be written as: $x_4(t) = 0.5 \,{\rm V} + Δx_4(t)$. | '''(4)''' The signal $x_4(t)$ can be written as: $x_4(t) = 0.5 \,{\rm V} + Δx_4(t)$. | ||
| − | *Here $Δx_4(t)$ denotes a | + | *Here $Δx_4(t)$ denotes a rectangular pulse with amplitude $0.5 \,{\rm V} $ and duration $4 \,{\rm ms} $, |
| + | *which due to its finite duration does not contribute to the DC signal component. | ||
*Therefore $A_0 \hspace{0.15cm}\underline{=0.5 \,{\rm V}}$ applies here. | *Therefore $A_0 \hspace{0.15cm}\underline{=0.5 \,{\rm V}}$ applies here. | ||
| Line 98: | Line 93: | ||
:$$A_0=\lim_{T_{\rm M}\to \infty}\frac{1}{T_{\rm M}}\int _{-T_{\rm M}/2}^{0}0 {\rm V} \cdot\, {\rm d } {\it t }+\lim_{T_{\rm M}\to \infty}\frac{1}{T_{\rm M}}\int _{0}^{+T_{\rm M}/2}1 \rm V \ {\rm d }{\it t }.$$ | :$$A_0=\lim_{T_{\rm M}\to \infty}\frac{1}{T_{\rm M}}\int _{-T_{\rm M}/2}^{0}0 {\rm V} \cdot\, {\rm d } {\it t }+\lim_{T_{\rm M}\to \infty}\frac{1}{T_{\rm M}}\int _{0}^{+T_{\rm M}/2}1 \rm V \ {\rm d }{\it t }.$$ | ||
| − | *Only the second term makes a contribution. From this follows again : $A_0 \hspace{0.15cm}\underline{=0.5 \,{\rm V}}$. | + | *Only the second term makes a contribution. From this follows again : $A_0 \hspace{0.15cm}\underline{=0.5 \,{\rm V}}$. |
{{ML-Fuß}} | {{ML-Fuß}} | ||
__NOEDITSECTION__ | __NOEDITSECTION__ | ||
| − | [[Category:Signal Representation: Exercises|^2.2 Direct Current | + | [[Category:Signal Representation: Exercises|^2.2 Direct Current Signal^]] |
Latest revision as of 17:30, 17 May 2021
The graph shows six time signals defined for all times $($from $-\infty$ to $+\infty)$. For all sample signals $x_i(t)$ the associated spectral function can be written as:
- $$X_i(f)=A_0\cdot{\rm \delta}(f)+\Delta X_i(f).$$
Here:
- $A_0$ is the DC component of the signal.
- $\Delta X_i(f)$ is the spectrum of the residual signal reduced by the DC component:
- $$\Delta x_i(t) = x_i(t) - A_0.$$
Hint:
- This exercise belongs to the chapter
Direct Current Signal - Limit Case of a Periodic Signal.
Questions
Solution
(1) The correct answers are 1, 3, 4, 5 and 6.
- All signals except $x_2(t)$ contain a DC signal component.
(2) Only solution 5 is correct:
- If the DC component $1\text{V}$ is subtracted from the signal $x_5(t)$, the residual signal $\Delta x_5(t) = x5(t) - 1\text{V}$ is zero.
- Accordignly, the spectral function is $\Delta X_5(f) = 0$.
- For all other time courses $\Delta x_i(t)ßne 0$ and thus the associated spectral function $\Delta X_i(f)\ne 0$, too.
(3) Given a periodic signal, averaging over a period duration is sufficient to calculate the DC signal component $A_0$ .
- For signal $x_3(t)$ the period duration is $T_0 = 3\,\text{ms}$. This results in the required DC component:$$A_0=\rm \frac{1}{3\,ms}\cdot \big[1\,V\cdot 1\,ms+(-1\,V)\cdot 2\,ms \big] \hspace{0.15cm}\underline{=-0.333\,V}.$$
(4) The signal $x_4(t)$ can be written as: $x_4(t) = 0.5 \,{\rm V} + Δx_4(t)$.
- Here $Δx_4(t)$ denotes a rectangular pulse with amplitude $0.5 \,{\rm V} $ and duration $4 \,{\rm ms} $,
- which due to its finite duration does not contribute to the DC signal component.
- Therefore $A_0 \hspace{0.15cm}\underline{=0.5 \,{\rm V}}$ applies here.
(5) The general equation for calculating the DC signal component is:
- $$A_0=\lim_{T_{\rm M}\to \infty}\frac{1}{T_{\rm M}}\int_{-T_{\rm M}/2}^{+T_{\rm M}/2}x(t)\, {\rm d }t.$$
- If one splits this integral into two partial integrals, one obtains:
- $$A_0=\lim_{T_{\rm M}\to \infty}\frac{1}{T_{\rm M}}\int _{-T_{\rm M}/2}^{0}0 {\rm V} \cdot\, {\rm d } {\it t }+\lim_{T_{\rm M}\to \infty}\frac{1}{T_{\rm M}}\int _{0}^{+T_{\rm M}/2}1 \rm V \ {\rm d }{\it t }.$$
- Only the second term makes a contribution. From this follows again : $A_0 \hspace{0.15cm}\underline{=0.5 \,{\rm V}}$.