Aufgaben:Exercise 1.4Z: Entropy of the AMI Code

• Return to book

Binary source signal (top) and
ternary encoder signal (bottom)

We assume similar prerequisites as in  task 1.4 :  

A binary source provides the source symbol sequence  $\langle q_\nu \rangle$  with  $q_\nu \in \{ {\rm L}, {\rm H} \}$, where there are no statistical ties between the individual sequence elements.

For the symbol probabilities, let:

• $p_{\rm L} =p_{\rm H} = 1/2$  (in subtasks 1 und 2),
• $p_{\rm L} = 1/4, \, p_{\rm H} = 3/4$  (subtasks 3, 4 and 5),
• $p_{\rm L} = 3/4, \, p_{\rm H} = 1/4$  (subtask 6).

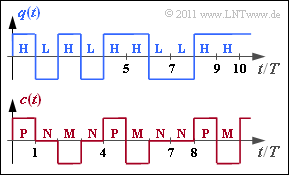
The presented code signal  $c(t)$  and the corresponding symbol sequence  $\langle c_\nu \rangle$  with  $c_\nu \in \{{\rm P}, {\rm N}, {\rm M} \}$  results from the AMI coding  (Alternate Mark Inversion)  according to the following rule:

• The binary symbol  $\rm L$  ⇒  Low  is always represented by the ternary symbol  $\rm N$  ⇒  Null .
• The binary symbol  $\rm H$  ⇒  High  is also coded deterministically but alternately (hence the name „AMI”) by the symbols  $\rm P$  ⇒  Plus  and  $\rm M$  ⇒  Minus .

In this task, the decision content  $H_0$  and the resulting entropy  $H_{\rm C}$  the code symbol sequence  $\langle c_\nu \rangle$  are to be determined for the three parameter sets mentioned above.  The relative redundancy of the code sequence results from this according to the equation

$$r_{\rm C} = \frac{H_{\rm 0}-H_{\rm C}}{H_{\rm C}} \hspace{0.05cm}.$$

Hints:

• The task belongs to the chapter  Sources with Memory.
• Reference is made in particular to the page  Die Entropie des AMI–Codes.

• In general, the following relations exist between the decision content  $H_0$,  the entropy  $H$  $($here equal to  $H_{\rm C})$  und den Entropienäherungen:

$$H \le \ \text{...} \ \le H_3 \le H_2 \le H_1 \le H_0 \hspace{0.05cm}.$$

• In  task 1.4  for equally probable symbols  $\rm L$  and  $\rm H$  the entropy approximations were calculated as follows (each in „bit/symbol”):

$$H_1 = 1.500\hspace{0.05cm},\hspace{0.2cm} H_2 = 1.375\hspace{0.05cm},\hspace{0.2cm}H_3 = 1.292 \hspace{0.05cm}.$$

Questions

1

Let the source symbols be equally probable  $(p_{\rm L} = p_{\rm H}= 1/2)$.  What is the entropy  $H_{\rm C}$  of the code symbol sequence  $\langle c_\nu \rangle$?

$H_{\rm C} \ = \ $ $\ \rm bit/ternary symbol$

2

What is the relative redundancy of the code symbol sequence?

$r_{\rm C} \ = \ $ $\ \rm \%$

3

For the binary source,  $p_{\rm L} = 1/4$  and  $p_{\rm H} = 3/4$.  What is the entropy of the code symbol sequence?

$H_{\rm C} \ = \ $ $\ \rm bit/ternary symbol$

4

What is the relative redundancy of the code symbol sequence?

$r_{\rm C} \ = \ $ $\ \rm \%$

5

Berechnen Sie die Näherung  $H_{\rm 1}$  der Coderentropie für  $p_{\rm L} = 1/4$  und  $p_{\rm H} = 3/4$.

$H_{\rm 1} \ = \ $ $\ \rm bit/ternary symbol$

6

Calculate the approximation  $H_{\rm 1}$  der Coderentropie für  $p_{\rm L} = 3/4$  und  $p_{\rm H} = 1/4$.

$H_{\rm 1} \ = \ $ $\ \rm bit/ternary symbol$

Solution

Solution

(1)  Since the AMI code neither adds new information nor causes information to disappear, the entropy  $H_{\rm C}$  of the code symbol sequence  $\langle c_\nu \rangle$  is equal to the source entropy  $H_{\rm Q}$. 

• Therefore, for equally probable and statistically independent source symbols, the following holds:

$$H_{\rm Q} {= 1 \,{\rm bit/Bin\ddot{a}rsymbol}} \hspace{0.3cm} \Rightarrow\hspace{0.3cm} H_{\rm C} \hspace{0.15cm} \underline {= 1 \,{\rm bit/Tern\ddot{a}rsymbol}} \hspace{0.05cm}.$$

(2)  The decision content of a ternary source is  $H_0 = \log_2 \; (3) = 1.585\; \rm bit/symbol$. 

• This gives the following for the relative redundancy

$$r_{\rm C} =1 -{H_{\rm C}/H_{\rm 0}}=1-1/{\rm log}_2\hspace{0.05cm}(3) \hspace{0.15cm} \underline {= 36.9 \,\%} \hspace{0.05cm}.$$

(3)    $H_{\rm C} = H_{\rm Q}$ is still valid.  However, because of the unequal symbol probabilities,  $H_{\rm Q}$  is now smaller:

$$H_{\rm Q} = \frac{1}{4} \cdot {\rm log}_2\hspace{0.05cm} (4) + \frac{3}{4} \cdot {\rm log}_2\hspace{0.1cm} (4/3) {= 0.811 \,{\rm bit/binary symbol}} \hspace{0.3cm} \Rightarrow\hspace{0.3cm} H_{\rm C} = H_{\rm Q} \hspace{0.15cm} \underline {= 0.811 \,{\rm bit/Tern\ddot{a}rsymbol}} \hspace{0.05cm}.$$

(4)  By analogy with sub-task  (2)    $r_{\rm C} = 1 - 0.811/1.585 \hspace{0.15cm} \underline {= 48.8 \,\%} \hspace{0.05cm} now holds.$

• One can generalise this result. Namely, it holds:

$$(1-0.488) = (1- 0.189) \cdot (1- 0.369)\hspace{0.3cm} \Rightarrow\hspace{0.3cm} (1-r_{\rm Codefolge}) = (1-r_{\rm Quelle}) \cdot (1- r_{\rm AMI-Code}) \hspace{0.05cm}.$$

(5)  Since each  $\rm L$  is mapped to  $\rm N$  and  $\rm H$  is mapped alternately to  $\rm M$  and  $\rm P$, it holds that

$$p_{\rm N} = p_{\rm L} = 1/4\hspace{0.05cm},\hspace{0.2cm}p_{\rm P} = p_{\rm M} = p_{\rm H}/2 = 3/8\hspace{0.3cm} \Rightarrow\hspace{0.3cm} H_1 = {1}/{4} \cdot {\rm log}_2\hspace{0.1cm} (4) + 2 \cdot {3}/{8} \cdot {\rm log}_2\hspace{0.1cm}(8/3) \hspace{0.15cm} \underline {= 1.56 \,{\rm bit/ternary symbol}} \hspace{0.05cm}.$$

(6)  Now the probabilities of occurrence of the ternary symbols are   $p_{\rm N} = 3/4$  sowie  $p_{\rm P} = p_{\rm M} =1/8$.  Thus:

$$H_1 = {3}/{4} \cdot {\rm log}_2\hspace{0.1cm} (4/3) + 2 \cdot {1}/{8} \cdot {\rm log}_2\hspace{0.1cm}(8) \hspace{0.15cm} \underline {= 1.06 \,{\rm bit/Tern\ddot{a}rsymbol}} \hspace{0.05cm}.$$

Interpretation:

• For  $p_{\rm L} = 1/4, \ p_{\rm H} = 3/4$  gives  $H_1 = 1.56 \; \rm bit/symbol$.
• For  $p_{\rm L} = 3/4, \ p_{\rm H} = 1/4$ , on the other hand,  $H_1 = 1.06 \; \rm bit/symbol$  results in a significantly smaller value.
• For both parameter combinations, however, the same applies:

$$H_0 = 1.585 \,{\rm bit/symbol}\hspace{0.05cm},\hspace{0.2cm}H_{\rm C} = \lim_{k \rightarrow \infty } H_k = 0.811 \,{\rm bit/Symbol} \hspace{0.05cm}.$$

It follows from this:

• If one considers two message sources  $\rm Q1$  and  $\rm Q2$  with the same symbol range  $M$   ⇒   decision content  $H_0 = \rm const.$, whereby the first-order entropy approximation  $\rm Q1$  is clearly greater for source  $(H_1)$  than for source  $\rm Q2$, one cannot conclude from this by any means that the entropy of  $\rm Q1$  is actually greater than the entropy of $\rm Q2$. 
• Rather, one must

• calculate enough entropy approximations  $H_1$,  $H_2$,  $H_3$,  ... for both sources and
• determine from them (graphically or analytically) the limit value of  $H_k$  für  $k \to \infty$  .

• Only then is a final statement about the entropy ratios possible.