Difference between revisions of "Aufgaben:Exercise 3.7Z: Rectangular Signal with Echo"
(Die Seite wurde neu angelegt: „ {{quiz-Header|Buchseite=Signaldarstellung/Faltungssatz und Faltungsoperation }} right| Wir betrachten ein periodisches R…“) |
m (Text replacement - "Dirac impulse" to "Dirac delta") |
||
| (27 intermediate revisions by 5 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Signal Representation/The Convolution Theorem and Operation |
}} | }} | ||
| − | [[File: | + | [[File:EN_Sig_Z_3_7.png|right|frame|Transmission signal $s(t)$, and <br>reception signal $r(t)$ with echo]] |
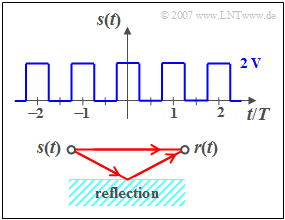
| − | + | We consider a periodic rectangular signal $s(t)$ with the possible amplitude values $0\text{ V}$ and $2\text{ V}$ and the period duration $T_0 = T = 1 \text{ ms}$. At the jump points, e.g. at $t = T/4$, the signal value are $1\text{ V}$. The DC component $($i.e. the Fourier coefficient $A_0)$ of the signal is $1\text{ V}$, too. | |
| − | : | + | Further applies: |
| − | + | * Due to symmetry (even function), all sine coefficients $B_n = 0$. | |
| − | + | * The coefficients $A_n$ with even $n$ are also zero. | |
| + | |||
| + | * For odd values of $n$, the following applies: | ||
:$$A_n = ( { - 1} )^{\left( {n - 1} \right)/2} \cdot \frac{{4\;{\rm{V}}}}{{n \cdot {\rm{\pi }}}}.$$ | :$$A_n = ( { - 1} )^{\left( {n - 1} \right)/2} \cdot \frac{{4\;{\rm{V}}}}{{n \cdot {\rm{\pi }}}}.$$ | ||
| − | + | ||
| + | The signal $s(t)$ reaches the receiver via two paths (see sketch below): | ||
| + | *Once on the direct path and secondly via a secondary path. | ||
| + | *The latter is characterised by the attenuation factor $\alpha$ and the transit time $\tau$ . | ||
| + | *Therefore, the following applies to the received signal: | ||
:$$r(t) = s(t) + \alpha \cdot s( {t - \tau } ).$$ | :$$r(t) = s(t) + \alpha \cdot s( {t - \tau } ).$$ | ||
| − | + | The frequency response of the channel is $H(f) = R(f)/S(f)$, the impulse response is denoted by $h(t)$ . | |
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| − | + | ''Hints:'' | |
| + | *This exercise belongs to the chapter [[Signal_Representation/The_Convolution_Theorem_and_Operation|The Convolution Theorem and Operation]]. | ||
| + | *Important information can be found on the page [[Signal_Representation/The_Convolution_Theorem_and_Operation#Convolution_of_a_function_with_a_Dirac_function|Convolution of a function with a Dirac function]]. | ||
| + | |||
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Which statements are true regarding the impulse response $h(t)$? |
|type="[]"} | |type="[]"} | ||
| − | - | + | - For $0 ≤ t < \tau$ holds $h(t) = 1$, and for $t > \tau$ holds $h(t) = 1 + \alpha$. |
| − | + | + | + It holds that $h(t) = \delta (t) + \alpha \cdot \delta(t - \tau)$. |
| − | - $h(t)$ | + | - $h(t)$ has a Gaussian shape. |
| − | { | + | {Calculate the reception signal $r(t)$ for the channel parameters $\alpha = -0.5$ and $\tau = T/4$. <br>What values result at the given times? |
|type="{}"} | |type="{}"} | ||
| − | $r(t = 0.2 \cdot T)$ | + | $r(t = 0.2 \cdot T)\ = \ $ { 1 3% } $\text{V}$ |
| − | $r(t = 0.3 \cdot T) | + | $r(t = 0.3 \cdot T)\ = \ $ { -1.03--0.97 } $\text{V}$ |
| − | { | + | {Calculate the reception signal $r(t)$ with $\alpha = 1$ and $\tau = T/2$. Interpret the result in the frequency domain. <br>What value results for $t = T/2$? |
|type="{}"} | |type="{}"} | ||
| − | $r(t = T/2)$ | + | $r(t = T/2)\ = \ $ { 2 3% } $\text{V}$ |
| Line 43: | Line 59: | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''1 | + | '''(1)''' The <u>second suggested solution</u> is correct: |
| + | *The impulse response is equal to the received signal $r(t)$, if a single Dirac delta is present at the input at time $t = 0$ : | ||
:$$h(t) = \delta (t) + \alpha \cdot \delta( {t - \tau } ).$$ | :$$h(t) = \delta (t) + \alpha \cdot \delta( {t - \tau } ).$$ | ||
| − | |||
| − | |||
| − | |||
| − | + | [[File:P_ID532__Sig_Z_3_7_b_neu.png|right|frame|Convolution of square wave signal $s(t)$ and impulse response $h(t)$]] | |
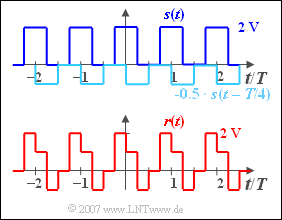
| + | '''(2)''' It holds $r(t) = s(t) ∗ h(t)$. This convolution operation is most easily performed graphically: | ||
| − | : | + | The values of the received signal are generally: |
| − | :* $0.25 < t/T < 0.50: r(t) = | + | * $0.00 < t/T < 0.25\text{:}\hspace{0.4cm} r(t) = +1\hspace{0.02cm}\text{ V}$, |
| + | * $0.25 < t/T < 0.50\text{:}\hspace{0.4cm} r(t) = -1 \hspace{0.02cm}\text{ V}$, | ||
| + | * $0.50 < t/T < 0.75\text{:}\hspace{0.4cm} r(t) = 0 \hspace{0.02cm}\text{ V}$, | ||
| + | * $0.75 < t/T < 1.00\text{:}\hspace{0.4cm} r(t) = +2 \hspace{0.02cm}\text{ V}$. | ||
| − | |||
| − | : | + | The values we are looking for are thus |
| + | :$$r(t = 0.2 \cdot T) \hspace{0.15cm}\underline{= +1 \hspace{0.02cm}\text{ V}},$$ | ||
| + | :$$r(t = 0.3 · T) \hspace{0.15cm}\underline{= -1 \hspace{0.02cm}\text{ V}}.$$ | ||
| − | |||
| − | '''3 | + | '''(3)''' Using a similar procedure as in '''(2)''', a direct signal $\rm (DC)$ of $2\hspace{0.02cm}\text{ V}$ is obtained for $r(t)$ : |
| + | *The gaps in the signal $s(t)$ are completely filled by the echo $s(t - T/2)$. | ||
| + | *This result can also be derived in the frequency domain. The channel frequency response is with $\alpha = 1$ and $\tau = T/2$: | ||
:$$H( f ) = 1 + 1 \cdot {\rm{e}}^{ - {\rm{j\pi }}fT} = 1 + \cos ( {{\rm{\pi }}fT} ) - {\rm{j}} \cdot {\rm{sin}}( {{\rm{\pi }}fT} ).$$ | :$$H( f ) = 1 + 1 \cdot {\rm{e}}^{ - {\rm{j\pi }}fT} = 1 + \cos ( {{\rm{\pi }}fT} ) - {\rm{j}} \cdot {\rm{sin}}( {{\rm{\pi }}fT} ).$$ | ||
| − | + | *Apart from the DC component, the input signal ${s(t)}$ only has components at $f = f_0 = 1/T$, $f = 3 \cdot f_0$, $f = 5 \cdot f_0$, etc.. | |
| + | *At these frequencies, however, both the real– and the imaginary part of ${H(f)}$ are equal to zero. | ||
| + | *Thus, for the output spectrum with $A_0 = 1 \text{ V}$ and $H(f = 0) = 2$ we obtain: | ||
:$$R(f) = A_0 \cdot H(f = 0) \cdot \delta (f) = 2\;{\rm{V}} \cdot \delta (f).$$ | :$$R(f) = A_0 \cdot H(f = 0) \cdot \delta (f) = 2\;{\rm{V}} \cdot \delta (f).$$ | ||
| − | + | The inverse Fourier transformation thus also yields $r(t) \underline{= 2 \text{ V= const}}$. | |
{{ML-Fuß}} | {{ML-Fuß}} | ||
__NOEDITSECTION__ | __NOEDITSECTION__ | ||
| − | [[Category: | + | [[Category:Signal Representation: Exercises|^3.4 The Convolution Theorem^]] |
Latest revision as of 08:05, 26 May 2021
We consider a periodic rectangular signal $s(t)$ with the possible amplitude values $0\text{ V}$ and $2\text{ V}$ and the period duration $T_0 = T = 1 \text{ ms}$. At the jump points, e.g. at $t = T/4$, the signal value are $1\text{ V}$. The DC component $($i.e. the Fourier coefficient $A_0)$ of the signal is $1\text{ V}$, too.
Further applies:
- Due to symmetry (even function), all sine coefficients $B_n = 0$.
- The coefficients $A_n$ with even $n$ are also zero.
- For odd values of $n$, the following applies:
- $$A_n = ( { - 1} )^{\left( {n - 1} \right)/2} \cdot \frac{{4\;{\rm{V}}}}{{n \cdot {\rm{\pi }}}}.$$
The signal $s(t)$ reaches the receiver via two paths (see sketch below):
- Once on the direct path and secondly via a secondary path.
- The latter is characterised by the attenuation factor $\alpha$ and the transit time $\tau$ .
- Therefore, the following applies to the received signal:
- $$r(t) = s(t) + \alpha \cdot s( {t - \tau } ).$$
The frequency response of the channel is $H(f) = R(f)/S(f)$, the impulse response is denoted by $h(t)$ .
Hints:
- This exercise belongs to the chapter The Convolution Theorem and Operation.
- Important information can be found on the page Convolution of a function with a Dirac function.
Questions
Solution
- The impulse response is equal to the received signal $r(t)$, if a single Dirac delta is present at the input at time $t = 0$ :
- $$h(t) = \delta (t) + \alpha \cdot \delta( {t - \tau } ).$$
(2) It holds $r(t) = s(t) ∗ h(t)$. This convolution operation is most easily performed graphically:
The values of the received signal are generally:
- $0.00 < t/T < 0.25\text{:}\hspace{0.4cm} r(t) = +1\hspace{0.02cm}\text{ V}$,
- $0.25 < t/T < 0.50\text{:}\hspace{0.4cm} r(t) = -1 \hspace{0.02cm}\text{ V}$,
- $0.50 < t/T < 0.75\text{:}\hspace{0.4cm} r(t) = 0 \hspace{0.02cm}\text{ V}$,
- $0.75 < t/T < 1.00\text{:}\hspace{0.4cm} r(t) = +2 \hspace{0.02cm}\text{ V}$.
The values we are looking for are thus
- $$r(t = 0.2 \cdot T) \hspace{0.15cm}\underline{= +1 \hspace{0.02cm}\text{ V}},$$
- $$r(t = 0.3 · T) \hspace{0.15cm}\underline{= -1 \hspace{0.02cm}\text{ V}}.$$
(3) Using a similar procedure as in (2), a direct signal $\rm (DC)$ of $2\hspace{0.02cm}\text{ V}$ is obtained for $r(t)$ :
- The gaps in the signal $s(t)$ are completely filled by the echo $s(t - T/2)$.
- This result can also be derived in the frequency domain. The channel frequency response is with $\alpha = 1$ and $\tau = T/2$:
- $$H( f ) = 1 + 1 \cdot {\rm{e}}^{ - {\rm{j\pi }}fT} = 1 + \cos ( {{\rm{\pi }}fT} ) - {\rm{j}} \cdot {\rm{sin}}( {{\rm{\pi }}fT} ).$$
- Apart from the DC component, the input signal ${s(t)}$ only has components at $f = f_0 = 1/T$, $f = 3 \cdot f_0$, $f = 5 \cdot f_0$, etc..
- At these frequencies, however, both the real– and the imaginary part of ${H(f)}$ are equal to zero.
- Thus, for the output spectrum with $A_0 = 1 \text{ V}$ and $H(f = 0) = 2$ we obtain:
- $$R(f) = A_0 \cdot H(f = 0) \cdot \delta (f) = 2\;{\rm{V}} \cdot \delta (f).$$
The inverse Fourier transformation thus also yields $r(t) \underline{= 2 \text{ V= const}}$.