Difference between revisions of "Applets:Dämpfung von Kupferkabeln"
David.Jobst (talk | contribs) |
m (Text replacement - "”" to """) |
||
| (60 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{ | + | {{LntAppletLink|attenuationCopperCables_en}} |
| − | {{ | + | |
| − | + | ==Programmbeschreibung== | |
| − | | | + | <br> |
| − | | | + | Dieses Applet berechnet die Dämpfungsfunktion $a_{\rm K}(f)$ von leitungsgebundenen Übertragungsmedien (jeweils mit der Kabellänge $l$): |
| − | }} | + | *Für Koaxialkabel verwendet man meist die Gleichung $a_{\rm K}(f)=(\alpha_0+\alpha_1\cdot f+\alpha_2\cdot \sqrt{f}) \cdot l$. |
| + | *Dagegen werden Zweidrahtleitungen oft in der Form $a_{\rm K}(f)=(k_1+k_2\cdot (f/{\rm MHz})^{k_3}) \cdot l$ dargestellt. | ||
| + | *Realisiert ist auch die Umrechnung der $(k_1, \ k_2, \ k_3)$–Darstellung in die $(\alpha_0, \ \alpha_1, \ \alpha_2)$–Form für $B = 30 \ \rm MHz$ und umgekehrt. | ||
| + | |||
| + | |||
| + | Außer der Dämpfungsfunktion $a_{\rm K}(f)$ können graphisch dargestellt werden: | ||
| + | *der zugehörige Betragsfrequenzgang $\left | H_{\rm K}(f)\right |=10^{-a_\text{K}(f)/20},$ | ||
| + | *der Entzerrer–Frequenzgang $\left | H_{\rm E}(f)\right | = \left | H_{\rm CRO}(f) / H_{\rm K}(f)\right | $, der zu einem Nyquist–Gesamtfrequenzgang $ H_{\rm CRO}(f) $ führt, | ||
| + | *der entsprechende Betrags–Quadrat–Frequenzgang $\left | H_{\rm E}(f)\right |^2 $. | ||
| + | |||
| + | |||
| + | Das Integral über $\left | H_{\rm E}(f)\right |^2 $ ist ein Maß für die Rauschüberhöhung des ausgewählten Nyquist–Gesamtfrequenzgangs und damit auch für zu erwartende Fehlerwahrscheinlichkeit. Aus dieser wird der ''Gesamt–Wirkungsgrad'' $\eta_\text{K+E}$ für '''K'''anal und '''E'''ntzerrer berechnet, der im Applet in $\rm dB$ ausgegeben wird. | ||
| + | |||
| + | |||
| + | Durch Optimierung des Roll-off–Faktors $r$ des Cosinus–Roll-off–Frequenzgangs $ H_{\rm CRO}(f) $ kommt man zum ''Kanal–Wirkungsgrad'' $ \eta_\text{K}$. Dieser gibt also die Verschlechterung des Gesamtsystems aufgrund der Dämpfungsfunktion $a_{\rm K}(f)$ des Übertragungsmediums an. | ||
| + | |||
| + | |||
| − | |||
| − | |||
==Theoretischer Hintergrund== | ==Theoretischer Hintergrund== | ||
| − | *Die Dämpfungsfunktion eines Koaxialkabels wird | + | <br> |
| − | $$ | + | ===Betragsfrequenzgang und Dämpfungsfunktion=== |
| − | *$ | + | Es besteht folgender Zusammenhang zwischen dem Betragsfrequenzgang und der Dämpfungsfunktion: |
| − | * | + | :$$\left | H_{\rm K}(f)\right |=10^{-a_\text{K}(f)/20} = {\rm e}^{-a_\text{K, Np}(f)}.$$ |
| − | *Der | + | *Der Index "K" soll deutlich machen, dass das betrachtete LZI–System ein '''K'''abel ist. |
| − | + | *Bei der ersten Berechnungsvorschrift ist die Dämpfungsfunktion $a_\text{K}(f)$ in $\rm dB$ (Dezibel) einzusetzen. | |
| − | + | *Bei der zweiten Berechnungsvorschrift ist die Dämpfungsfunktion $a_\text{K, Np}(f)$ in $\rm Np$ (Neper) einzusetzen. | |
| − | $$ | + | * Es gelten folgende Umrechnungen $\rm 1 \ dB = 0.05 \cdot \ln (10) \ Np= 0.1151 \ Np$ bzw. $\rm 1 \ Np = 20 \cdot \lg (e) \ dB= 8.6859 \ dB$. |
| − | + | * In diesem Applet werden ausschließlich die dB–Werte verwendet. | |
| + | |||
| + | ===Dämpfungsfunktion eines Koaxialkabels=== | ||
| + | Die Dämpfungsfunktion eines Koaxialkabels der Länge $l$ wird in [Wel77]<ref name ='Wel77'>Wellhausen, H. W.: Dämpfung, Phase und Laufzeiten bei Weitverkehrs–Koaxialpaaren. Frequenz 31, S. 23-28, 1977.</ref> wie folgt angegeben: | ||
| + | :$$a_{\rm K}(f)=(\alpha_0+\alpha_1\cdot f+\alpha_2\cdot \sqrt{f}) \cdot l.$$ | ||
| + | *Beachten Sie bitte den Unterschied zwischen der Dämpfungsfunktion $a_{\rm K}(f)$ in $\rm dB$ und den "alpha"–Koeffizienten $\alpha_{\rm K}(f)=a_{\rm K}(f)/l$ mit anderen Pseudo–Einheiten. | ||
| + | *Die Dämpfungsfunktion $a_{\rm K}(f)$ ist direkt proportional zur Kabellänge $l$. Man bezeichnet den Quotienten $a_{\rm K}(f)/l$ als "Dämpfungsmaß" oder "kilometrische Dämpfung". | ||
| + | *Der frequenzunabhängige Anteil $α_0$ des Dämpfungsmaßes berücksichtigt die Ohmschen Verluste ("Leitungsverluste"). | ||
| + | *Der frequenzproportionale Anteil $α_1 · f$ des Dämpfungsmaßes ist auf die Ableitungsverluste ("Querverluste") zurückzuführen. | ||
| + | *Der dominante Anteil $α_2$ geht auf den [[Digital_Signal_Transmission/Ursachen_und_Auswirkungen_von_Impulsinterferenzen#Frequenzgang_eines_Koaxialkabels|Skineffekt]] zurück, der bewirkt, dass bei höherfrequentem Wechselstrom die Stromdichte im Leiterinneren niedriger ist als an der Oberfläche. Dadurch steigt der Widerstandsbelag einer elektrischen Leitung mit der Wurzel aus der Frequenz an. | ||
| + | |||
| + | |||
| + | Die Konstanten für das ''Normalkoaxialkabel'' mit 2.6 mm Innendurchmesser und 9.5 mm Außendurchmesser ⇒ kurz '''Coax (2.6/9.5 mm)''' lauten: | ||
| + | :$$\alpha_0 = 0.014\, \frac{ {\rm dB} }{ {\rm km} }\hspace{0.05cm}, \hspace{0.2cm} \alpha_1 = 0.0038\, \frac{ {\rm dB} }{ {\rm km \cdot MHz} }\hspace{0.05cm}, \hspace{0.2cm} \alpha_2 = 2.36\, \frac{ {\rm dB} }{ {\rm km \cdot \sqrt{MHz} } }\hspace{0.05cm}.$$ | ||
| + | |||
| + | Entsprechend gilt für das ''Kleinkoaxialkabel'' ⇒ kurz '''Coax (1.2/4.4 mm)''': | ||
| + | :$$\alpha_0 = 0.068\, \frac{ {\rm dB} }{ {\rm km} }\hspace{0.05cm}, \hspace{0.2cm} | ||
| + | \alpha_1 = 0.0039\, \frac{ {\rm dB} }{ {\rm km \cdot MHz} }\hspace{0.05cm}, \hspace{0.2cm} \alpha_2 =5.2\, \frac{ {\rm dB} }{ {\rm km \cdot \sqrt{MHz} } }\hspace{0.05cm}.$$ | ||
| + | |||
| + | |||
| + | Diese Werte können aus den geometrischen Abmessungen der Kabel berechnet werden und wurden durch Messungen am Fernmeldetechnischen Zentralamt in Darmstadt bestätigt – siehe [Wel77]<ref name ='Wel77'>Wellhausen, H. W.: Dämpfung, Phase und Laufzeiten bei Weitverkehrs–Koaxialpaaren. Frequenz 31, S. 23-28, 1977.</ref> . Sie gelten für eine Temperatur von 20°C (293 K) und Frequenzen größer als 200 kHz. | ||
| + | |||
| + | |||
| + | ===Dämpfungsfunktion einer Zweidrahtleitung=== | ||
| + | Die Dämpfungsfunktion einer Zweidrahtleitung (englisch: ''Two–wired Line'') der Länge $l$ wird in [PW95]<ref name ='PW95'>Pollakowski, M.; Wellhausen, H.W.: Eigenschaften symmetrischer Ortsanschlusskabel im Frequenzbereich bis 30 MHz. Mitteilung aus dem Forschungs- und Technologiezentrum der Deutschen Telekom AG, Darmstadt, Verlag für Wissenschaft und Leben Georg Heidecker, 1995.</ref> wie folgt angegeben: | ||
| + | :$$a_{\rm K}(f)=(k_1+k_2\cdot (f/{\rm MHz})^{k_3}) \cdot l.$$ | ||
| + | Dieser Funktionsverlauf ist nicht direkt interpretierbar, sondern es handelt sich um eine phänomenologische Beschreibungsform. | ||
| + | |||
| + | Ebenfalls in [PW95]<ref name ='PW95'>Pollakowski, M.; Wellhausen, H.W.: Eigenschaften symmetrischer Ortsanschlusskabel im Frequenzbereich bis 30 MHz. Mitteilung aus dem Forschungs- und Technologiezentrum der Deutschen Telekom AG, Darmstadt, Verlag für Wissenschaft und Leben Georg Heidecker, 1995.</ref>findet man die aus Messergebnissen ermittelten Konstanten für verschiedene Leitungsdurchmesser $d$: | ||
| + | * $d = 0.35 \ {\rm mm}$: $k_1 = 7.9 \ {\rm dB/km}, \hspace{0.2cm}k_2 = 15.1 \ {\rm dB/km}, \hspace{0.2cm}k_3 = 0.62$, | ||
| + | * $d = 0.40 \ {\rm mm}$: $k_1 = 5.1 \ {\rm dB/km}, \hspace{0.2cm}k_2 = 14.3 \ {\rm dB/km}, \hspace{0.2cm}k_3 = 0.59$, | ||
| + | * $d = 0.50 \ {\rm mm}$: $k_1 = 4.4 \ {\rm dB/km}, \hspace{0.2cm}k_2 = 10.8 \ {\rm dB/km}, \hspace{0.2cm}k_3 = 0.60$, | ||
| + | * $d = 0.60 \ {\rm mm}$: $k_1 = 3.8 \ {\rm dB/km}, \hspace{0.2cm}k_2 = \hspace{0.25cm}9.2 \ {\rm dB/km}, \hspace{0.2cm}k_3 = 0.61$. | ||
| + | |||
| + | |||
| + | Man erkennt aus diesen Zahlenwerten: | ||
| + | *Dämpfungsmaß $α(f)$ und Dämpfungsfunktion $a_{\rm K}(f) = α(f) · l$ hängen signifikant vom Leitungsdurchmesser ab. Die seit 1994 verlegten Kabel mit $d = 0.35$ mm und $d = 0.5$ mm haben etwa ein um $10\%$ größeres Dämpfungsmaß als die älteren Leitungen mit $d = 0.4$bzw. $0.6$ mm. | ||
| + | *Dieser mit den Herstellungs– und Verlegungskosten begründete kleinere Durchmesser vermindert allerdings die Reichweite $l_{\rm max}$ der auf diesen Leitungen eingesetzten Übertragungssysteme signifikant, so dass im schlimmsten Fall teuere Zwischenregeneratoren eingesetzt werden müssen. | ||
| + | *Die heute üblichen Übertragungsverfahren für Kupferleitungen belegen allerdings nur ein relativ schmales Frequenzband, zum Beispiel sind dies bei [[Examples_of_Communication_Systems/Allgemeine_Beschreibung_von_ISDN|ISDN]] $120\ \rm kHz$ und bei [[Examples_of_Communication_Systems/Allgemeine_Beschreibung_von_DSL|DSL]] ca. $1100 \ \rm kHz$. Für $f = 1 \ \rm MHz$ beträgt das Dämpfungsmaß für ein 0.4 mm–Kabel etwa $20 \ \rm dB/km$, so dass selbst bei einer Kabellänge von $l = 4 \ \rm km$ der Dämpfungswert nicht über $80 \ \rm dB$ liegt. | ||
| + | |||
| + | |||
| + | ===Umrechnung zwischen $k$– und $\alpha$– Parametern=== | ||
| + | Es besteht die Möglichkeit, die $k$–Parameter des Dämpfungsmaßes ⇒ $\alpha_{\rm I} (f)$ in entsprechende $\alpha$–Parameter ⇒ $\alpha_{\rm II} (f)$ umzurechnen: | ||
| + | :$$\alpha_{\rm I} (f) = k_1 + k_2 \cdot (f/f_0)^{k_3}\hspace{0.05cm}, \hspace{0.2cm}{\rm mit} \hspace{0.15cm} f_0 = 1\,{\rm MHz},$$ | ||
| + | :$$\alpha_{\rm II} (f) = \alpha_0 + \alpha_1 \cdot f + \alpha_2 \cdot \sqrt {f}.$$ | ||
| + | |||
| + | Als Kriterium dieser Umrechnung gehen wir davon aus, dass die quadratische Abweichung dieser beiden Funktionen innerhalb einer Bandbreite $B$ minimal ist: | ||
| + | :$$\int_{0}^{B} \left [ \alpha_{\rm I} (f) - \alpha_{\rm II} (f)\right ]^2 \hspace{0.1cm}{\rm d}f \hspace{0.3cm}\Rightarrow \hspace{0.3cm}{\rm Minimum} \hspace{0.05cm} .$$ | ||
| + | Es ist offensichtlich, dass $α_0 = k_1$ gelten wird. Die Parameter $α_1$ und $α_2$ sind von der zugrundegelegten Bandbreite $B$ abhängig und lauten: | ||
| + | :$$\begin{align*}\alpha_1 & = 15 \cdot (B/f_0)^{k_3 -1}\cdot \frac{k_3 -0.5}{(k_3 + 1.5)(k_3 + 2)}\cdot {k_2}/{ {f_0} }\hspace{0.05cm} ,\\ \alpha_2 & = 10 \cdot (B/f_0)^{k_3 -0.5}\cdot \frac{1-k_3}{(k_3 + 1.5)(k_3 + 2)}\cdot {k_2}/{\sqrt{f_0} }\hspace{0.05cm} .\end{align*}$$ | ||
| + | |||
| + | In der Gegenrichtung lautet die Umrechnungsvorschrift für den Exponenten: | ||
| + | |||
| + | :$$k_3 = \frac{A + 0.5} {A +1}, \hspace{0.2cm}\text{Hilfsgröße: }A = \frac{2} {3} \cdot \frac{\alpha_1 \cdot \sqrt{f_0}}{\alpha_2} \cdot \sqrt{B/f_0}.$$ | ||
| + | |||
| + | Mit diesem Ergebnis lässt sich $k_2$ mit jeder der oberen Gleichungen angeben. | ||
| + | |||
| + | {{GraueBox|TEXT= | ||
| + | $\text{Beispiel 1:}$ Im Folgenden verwenden wir die Normierunggröße $f_0 = 1 \ \rm MHz$. | ||
| + | *Für $k_3 = 1$ (frequenzproportionales Dämpfungsmaß) ergeben sich folgerichtig $\alpha_0 = k_0\hspace{0.05cm} ,\hspace{0.2cm} \alpha_1 = {k_2}/{ {f_0} }\hspace{0.05cm} ,\hspace{0.2cm} \alpha_2 = 0\hspace{0.05cm} .$ | ||
| + | *Für $k_3 = 0.5$ (entsprechend Skineffekt) erhält man folgende Koeffizienten: $\alpha_0 = k_0\hspace{0.05cm} ,\hspace{0.2cm}\alpha_1 = 0\hspace{0.05cm} ,\hspace{0.2cm} \alpha_2 = {k_2}/{\sqrt{f_0} }\hspace{0.05cm}.$ | ||
| + | *Für $k_3 < 0.5$ ergibt sich ein negatives $\alpha_1$. Umrechnung ist nur für $0.5 \le k_3 \le 1$ möglich. | ||
| + | *Für $0.5 \le k_3 \le$ ergeben sich Koeffizienten $\alpha_1 > 0$ und $\alpha_2 > 0$, die auch von $B/f_0$ abhängen. | ||
| + | *Aus $\alpha_1 = 0.3\, {\rm dB}/ ({\rm km \cdot MHz}) \hspace{0.05cm}, \hspace{0.2cm} \alpha_2 = 3\, {\rm dB}/ ({\rm km \cdot \sqrt{MHz} })\hspace{0.05cm},\hspace{0.2cm}B = 30 \ \rm MHz$ folgt $k_3 = 0.63$ und $k_2 = 2.9 \ \rm dB/km$.}} | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | ===Zum Kanaleinfluss auf die binäre Nyquistentzerrung=== | ||
| + | [[File:Applet_Kabeldaempfung_1_version3.png|right|frame|Vereinfachtes Blockschaltbild des optimalen Nyquistentzerrers|class=fit]] | ||
| + | Wir gehen vom skizzierten Blockschaltbild aus. Zwischen der Diracquelle und dem Entscheider liegen die Frequenzgänge für Sender ⇒ $H_{\rm S}(f)$, Kanal ⇒ $H_{\rm K}(f)$ und Empfänger ⇒ $H_{\rm E}(f)$. | ||
| + | |||
| + | In diesem Applet | ||
| + | *vernachlässigen wir den Einfluss der Sendeimpulsform ⇒ $H_{\rm S}(f) \equiv 1$ ⇒ diracförmiges Sendesignal $s(t)$, | ||
| + | *setzen ein binäres Nyquistsystem mit Cosinus–Roll-off um die Nyquistfrequenz $f_{\rm Nyq} = [f_1 + f_2]/2 =1(2T)$ voraus: | ||
| + | :$$H_{\rm K}(f) · H_{\rm E}(f) = H_{\rm CRO}(f).$$ | ||
| + | |||
| + | [[File:Applet_Kabeldaempfung_2_version2.png|right|frame|Frequenzgang mit Cosinus–Roll-off|class=fit]] | ||
| + | |||
| + | Das bedeutet: Das [[Digital_Signal_Transmission/Eigenschaften_von_Nyquistsystemen#Erstes_Nyquistkriterium_im_Frequenzbereich|erste Nyquistkriterium]] wird erfüllt ⇒ zeitlich aufeinander folgende Impulse stören sich nicht gegenseitig ⇒ es gibt keine [[Digital_Signal_Transmission/Ursachen_und_Auswirkungen_von_Impulsinterferenzen|Impulsinterferenzen]] (englisch: ''Intersymbol Interference'', ISI). | ||
| + | |||
| + | Bei weißem Rauschen wird somit die Übertragungsqualität allein durch die Rauschleistung vor dem Empfänger bestimmt: | ||
| + | |||
| + | :$$P_{\rm N} =\frac{N_0}{2} \cdot \int_{-\infty}^{+\infty} |H_{\rm E}(f)|^2 \ {\rm d}f\hspace{1cm}\text{mit}\hspace{1cm}|H_{\rm E}(f)|^2 = \frac{|H_{\rm CRO}(f)|^2}{|H_{\rm K}(f)|^2}.$$ | ||
| + | <br clear=all> | ||
| + | Die kleinstmögliche Rauschleistung ergibt sich bei idealem Kanal ⇒ $H_{\rm K}(f) \equiv 1$ und gleichzeitig dem Frequenzgang $H_{\rm CRO}(f)$ mit Roll-off–Faktor $r = 1$ im Bereich $|f| \le 2 \cdot f_{\rm Nyq}$ (siehe Skizze): | ||
| + | |||
| + | :$$P_\text{N, min} = P_{\rm N} \ \big [\text{optimales System: }H_{\rm K}(f) \equiv 1; \ \text{ Roll-off–Faktor } r=r_{\rm opt} =1 \big ] = N_0 \cdot 3/4 \cdot f_{\rm Nyq} .$$ | ||
| + | |||
| + | {{BlaueBox|TEXT= | ||
| + | $\text{Definitionen:}$ | ||
| + | *Als Gütekriterium für ein gegebenes System verwenden wir den '''Gesamt–Wirkungsgrad''': | ||
| + | |||
| + | :$$\eta_\text{K+E} = \frac{P_{\rm N} \ \big [\text{optimales System: }H_{\rm K}(f) \equiv 1, \ r=r_{\rm opt} =1 \big ]}{P_{\rm N} \ \big [\text{gegebenes System: Kanal }H_{\rm K}(f), \ \text{Roll-off-Faktor }r \big ]} =\left [ \frac{1}{3/4 \cdot f_{\rm Nyq} } \cdot \int_{0}^{+\infty} \vert H_{\rm E}(f) \vert^2 \ {\rm d}f \right ]^{-1}\le 1.$$ | ||
| + | |||
| + | :Diese Systemgröße wird im Applet für beide Parametersätze in logarithmierter Form angegeben: $10 \cdot \lg \ \eta_\text{K+E} \le 0 \ \rm dB$. | ||
| + | |||
| + | *Durch Variation und Optimierung des Roll-off-Faktors $r$ erhält man den '''Kanal–Wirkungsgrad''': | ||
| + | |||
| + | :$$\eta_\text{K} = \max_{0 \le r \le 1} \ \eta_\text{K+E} .$$}} | ||
| + | |||
| + | |||
| + | [[File:Applet_Kabeldaempfung_3_version2.png|right|frame|Betrags–Quadrat–Frequenzgang $\left \vert H_{\rm E}(f)\right \vert ^2 $|class=fit]] | ||
| + | {{GraueBox|TEXT= | ||
| + | $\text{Beispiel 2:}$ | ||
| + | Die Grafik zeigt den Betrags–Quadrat–Frequenzgang $\left \vert H_{\rm E}(f)\right \vert ^2 $ mit $\left \vert H_{\rm E}(f)\right \vert = H_{\rm CRO}(f) / \left \vert H_{\rm K}(f)\right \vert$ für folgende Randbedingungen: | ||
| + | *Dämpfungsfunktion des Kanals: $a_{\rm K}(f) = 1 \ {\rm dB} \cdot \sqrt{f/\ {\rm MHz} }$, | ||
| + | *Nyquist–Frequenz: : $f_{\rm Nyq} = 20 \ {\rm MHz}$, Roll-off-Faktor $r = 0.5$ | ||
| + | |||
| + | |||
| + | Daraus ergeben sich folgende Konsequenzen: | ||
| + | *Im Bereich bis $f_{1} = 10 \ {\rm MHz}$ ist $H_{\rm CRO}(f) = 1$ ⇒ $\left \vert H_{\rm E}(f)\right \vert ^2 = \left \vert H_{\rm K}(f)\right \vert ^{-2}$ (siehe gelbe Hinterlegung). | ||
| + | *Erst im Bereich von $f_{1}$ bis $f_{2} = 30 \ {\rm MHz}$ ist die Flanke von $H_{\rm CRO}(f)$ wirksam und $\left \vert H_{\rm E}(f)\right \vert ^2$ wird immer kleiner. | ||
| + | *Das Maximum von $\left \vert H_{\rm E}(f_{\rm max})\right \vert ^2$ bei $f_{\rm max} \approx 11.5 \ {\rm MHz}$ ist mehr als doppelt so groß wie $\left \vert H_{\rm E}(f = 0)\right \vert ^2 = 1$. | ||
| + | *Das Integral über $\left \vert H_{\rm E}(f)\right \vert ^2$ ist ein Maß für die wirksame Rauschleistung. Diese ist im Beispiel um den Faktor $4.6$ größer als die minimale Rauschleistung (für $a_{\rm K}(f) = 0 \ {\rm dB}$ und $r=1$) ⇒ $10 \cdot \lg \ \eta_\text{K+E} \approx - 6.6 \ {\rm dB}.$}} | ||
| + | |||
| + | |||
| + | ==Versuchsdurchführung== | ||
| + | |||
| + | [[File:Applet_Kabeldaempfung_6_version1.png|right]] | ||
| + | *Wählen Sie zunächst die Nummer '''1''' ... '''11''' der zu bearbeitenden Aufgabe. | ||
| + | *Der Aufgabentext wird angezeigt. Die Parameterwerte sind angepasst. | ||
| + | *Lösung nach Drücken von "Hide solution". | ||
| + | *Aufgabenstellung und Lösung in Englisch. | ||
| + | |||
| + | |||
| + | Die Nummer '''0''' entspricht einem "Reset": | ||
| + | *Gleiche Einstellung wie beim Programmstart. | ||
| + | *Ausgabe eines "Reset–Textes" mit weiteren Erläuterungen zum Applet. | ||
| + | |||
| + | |||
| + | In der folgenden Beschreibung bezeichnet '''Blue''' den linken Parametersatz (im Applet blau markiert) '''Red''' den rechten Parametersatz (im Applet rot markiert). Alle Angaben mit Hochkomma sind ohne Einheit, zum Beispiel steht ${\alpha_2}' =2$ für $\alpha_2 =2\, {\rm dB} / ({\rm km \cdot \sqrt{MHz} })$. | ||
| + | |||
| + | |||
| + | {{BlaueBox|TEXT= | ||
| + | '''(1)''' Setzen Sie '''Blue''' zunächst auf $\text{Coax (1.2/4.4 mm)}$ und anschließend auf $\text{Coax (2.6/9.5 mm)}$. Die Kabellänge sei jeweils $l_{\rm Blue}= 5\ \rm km$. | ||
| + | :Betrachten und Interpretieren Sie $a_{\rm K}(f)$ und $\vert H_{\rm K}(f) \vert$, insbesondere die Funktionswerte $a_{\rm K}(f = f_\star = 30 \ \rm MHz)$ und $\vert H_{\rm K}(f = 0) \vert$.}} | ||
| + | |||
| + | |||
| + | $\Rightarrow\hspace{0.3cm}\text{Näherungsweise steigt die Dämpfungsfunktion mit }\sqrt{f}\text{ und der Betragsfrequenzgang fällt ähnlich einer Exponentialfunktion};$ | ||
| + | |||
| + | $\hspace{1.15cm}\text{Coax (1.2/4.4 mm): }a_{\rm K}(f = f_\star) = 143.3\text{ dB;}\hspace{0.5cm}\vert H_{\rm K}(f = 0) \vert = 0.96.$ | ||
| + | |||
| + | $\hspace{1.15cm}\text{Coax (2.6/9.5 mm): }a_{\rm K}(f = f_\star) = 65.3\text{ dB;}\hspace{0.5cm}\vert H_{\rm K}(f = 0) \vert = 0.99;$ | ||
| + | |||
| + | |||
| + | {{BlaueBox|TEXT= | ||
| + | '''(2)''' Für '''Blue''' gelte $\text{Coax (2.6/9.5 mm)}$ und $l_{\rm Blue} = 5\ \rm km$. Wie wird $a_{\rm K}(f =f_\star = 30 \ \rm MHz)$ von $\alpha_0$, $\alpha_1$ und $\alpha_2$ beeinflusst?}} | ||
| + | |||
| + | |||
| + | $\Rightarrow\hspace{0.3cm}\text{Entscheidend ist }\alpha_2\text{ (Skineffekt). Die Beitrag von } \alpha_0\text{ ist nur ca. 0.1 dB und der von }\alpha_1 \text{ nur ca. 0.6 dB.}$ | ||
| + | |||
| + | |||
| + | {{BlaueBox|TEXT= | ||
| + | '''(3)''' Setzen Sie zusätzlich '''Red''' auf $\text{Two–wired Line (0.5 mm)}$ und $l_{\rm Red} = 1\ \rm km$. Welcher Wert ergibt sich für $a_{\rm K}(f =f_\star= 30 \ \rm MHz)$? | ||
| + | :Bis zu welcher Länge $l_{\rm Red}$ ist die rote Dämpfungsfunktion vergleichbar mit der blauen?}} | ||
| + | |||
| + | |||
| + | $\Rightarrow\hspace{0.3cm}\text{Für die rote Kurve gilt: }a_{\rm K}(f = f_\star) = 87.5 {\ \rm dB} \text{. Obige Bedingung wird erfüllt für }l_{\rm Red} = 0.7\ {\rm km} \ \Rightarrow \ a_{\rm K}(f = f_\star) = 61.3 {\ \rm dB}.$ | ||
| + | |||
| + | |||
| + | {{BlaueBox|TEXT= | ||
| + | '''(4)''' Setzen Sie '''Red''' auf ${k_1}' = 0, {k_2}' = 10, {k_3}' = 0.75, {l_{\rm red} } = 1 \ \rm km$ und variieren Sie den Parameter $0.5 \le k_3 \le 1$. | ||
| + | :Was erkennt man anhand von $a_{\rm K}(f)$ und $\vert H_{\rm K}(f) \vert$? }} | ||
| + | |||
| + | |||
| + | $\Rightarrow\hspace{0.3cm}\text{Bei festem }k_2\text {wird }a_{\rm K}(f)\text{ mit größerem }k_3\text{ immer größer und }\vert H_{\rm K}(f) \vert \text{ nimmt immer schneller ab. Mit }k_3 =1: a_{\rm K}(f)\text{ steigt linear.}$ | ||
| + | |||
| + | $\hspace{1.15cm}\text{Mit }k_3 \to 0.5\text{ wird die Dämpfungsfunktion wie beim Koaxialkabel immer mehr durch den Skineffekt bestimmt.}$ | ||
| + | |||
| + | |||
| + | {{BlaueBox|TEXT= | ||
| + | '''(5)''' Setzen Sie '''Red''' auf $\text{Two–wired Line (0.5 mm)}$ und '''Blue''' auf $\text{Conversion of Red}$. Es gelte $l_{\rm Red} = l_{\rm Blue} = 1\ \rm km$. | ||
| + | :Betrachten und interpretieren Sie die dargestellten Funktionsverläufe für $a_{\rm K}(f)$ und $\vert H_{\rm K}(f) \vert$.}} | ||
| + | |||
| + | |||
| + | $\Rightarrow\hspace{0.3cm}\text{Sehr gute Approximation der Zweidrahtleitung durch den blauen Parametersatz, sowohl bezüglich }a_{\rm K}(f) \text{ als auch }\vert H_{\rm K}(f) \vert.$ | ||
| + | |||
| + | $\hspace{1.15cm}\text{Die errechneten Parameterwerte nach der Konvertierung sind }{\alpha_0}' = {k_1}' = 4.4, \ {\alpha_1}' = 0.76, \ {\alpha_2}' = 11.12.$ | ||
| + | |||
| + | |||
| + | {{BlaueBox|TEXT= | ||
| + | '''(6)''' Es gelten die Einstellungen von '''(5)'''. Welche Anteile der Dämpfungsfunktion gehen auf Ohmschen Verlust, Querverluste und Skineffekt zurück? }} | ||
| + | |||
| + | |||
| + | $\Rightarrow\hspace{0.3cm}\text{Lösung anhand '''Blue''': }a_{\rm K}(f = f_\star= 30 \ {\rm MHz}) = 88.1\ {\rm dB}, \hspace{0.2cm}\text{ohne }\alpha_0\text{: }83.7\ {\rm dB}, \hspace{0.2cm}\text{ohne }\alpha_0 \text{ und } \alpha_1\text{: }60.9\ {\rm dB}.$ | ||
| + | |||
| + | $\hspace{1.15cm}\text{Bei einer Zweidrahtleitung ist der Einfluss der Längs– und der Querverluste signifikant größer als bei einem Koaxialkabel.}$ | ||
| + | |||
| + | |||
| + | |||
| + | {{BlaueBox|TEXT= | ||
| + | '''(7)''' Setzen Sie '''Blue''' auf ${\alpha_0}' = {\alpha_1}' ={\alpha_2}' = 0$ und '''Red''' auf ${k_1}' = 2, {k_2}' = 0, {l_{\rm red} } = 1 \ \rm km$. Zusätzlich gelte ${f_{\rm Nyq} }' =15$ und $r= 0.5$. | ||
| + | :Wie groß ist jeweils der Gesamt–Wirkungsgrad $\eta_\text{K+E}$ und der Kanal–Wirkungsgrad $\eta_\text{K}$?}} | ||
| + | |||
| + | |||
| + | $\Rightarrow\hspace{0.3cm}\text{Es gilt }10 \cdot \lg \ \eta_\text{K+E} = -0.7\ \ {\rm dB}\text{ (Blue: ideales System) und }10 \cdot \lg \ \eta_\text{K+E} = -2.7\ \ {\rm dB}\text{ (Red: nur Gleichsignaldämpfung)}$. | ||
| + | |||
| + | $\hspace{0.95cm}\text{Der bestmögliche Rolloff–Faktor ist }r = 1.\text{ Somit ist }10 \cdot \lg \ \eta_\text{K} = 0 \ {\rm dB}\text{ (Blue) bzw. }10 \cdot \lg \ \eta_\text{K} = -2\ {\rm dB}\text{ (Red)}.$ | ||
| + | |||
| + | |||
| + | {{BlaueBox|TEXT= | ||
| + | '''(8)''' Es gilt die Einstellung von '''(7)'''. Mit welcher Sendeleistung $P_{\rm red}$ in Bezug zu $P_{\rm blue}$ erreichen beide Systeme gleiche Fehlerwahrscheinlichkeit? }} | ||
| + | |||
| + | |||
| + | $\Rightarrow\hspace{0.3cm}\text{Es muss gelten: }10 \cdot \lg \ P_{\rm red}/P_{\rm blue} =2 \ {\rm dB} \ \ \text{ ⇒ } \ \ P_{\rm red}/P_{\rm blue} = 10^{0.2} = 1.585.$ | ||
| + | |||
| + | |||
| + | {{BlaueBox|TEXT= | ||
| + | '''(9)''' Setzen Sie '''Blue''' auf ${\alpha_0}' = {\alpha_1}' = 0, \ {\alpha_2}' = 3, \ {l_{\rm blue} }' = 2$ und '''Red''' auf "Inactive". Zusätzlich gelte ${f_{\rm Nyq} }' =15$ und $r= 0.7$. | ||
| + | :Welchen Verlauf hat $\vert H_{\rm E}(f) \vert$? Wie groß ist sind Gesamt–Wirkungsgrad $\eta_\text{K+E}$ und Kanal–Wirkungsgrad $\eta_\text{K}$?}} | ||
| + | |||
| + | |||
| + | $\Rightarrow\hspace{0.3cm}\text{Für } f < 7.5 {\ \rm MHz}\text{ ist } \vert H_{\rm E}(f) \vert = \vert H_{\rm K}(f) \vert ^{-1}.\text{ Für }(f > 22.5 {\ \rm MHz)}\text{ ist: }\vert H_{\rm E}(f) \vert = 0.\text{ Dazwischen Einfluss der CRO–Flanke.}$ | ||
| + | |||
| + | $\hspace{0.95cm}\text{Der bestmögliche Rolloff–Faktor }r = 0.7\text{ ist bereits eingestellt: }\Rightarrow \ 10 \cdot \lg \ \eta_\text{K+E} = 10 \cdot \lg \ \eta_\text{K} \approx - 18.1 \ {\rm dB}.$ | ||
| + | |||
| + | |||
| + | {{BlaueBox|TEXT= | ||
| + | '''(10)''' Setzen Sie '''Blue''' auf ${\alpha_0}' = {\alpha_1}' = 0, \ {\alpha_2}' = 3, \ {l_{\rm blue} }' = 8$ sowie '''Red''' auf "Inactive". Zusätzlich gelte ${f_{\rm Nyq} }' =15$ und $r= 0.7$. | ||
| + | :Welchen Wert hat $\vert H_{\rm E}(f = 0) \vert$? Was ist der Maximalwert von $\vert H_{\rm E}(f) \vert$? Wie groß ist ist der Kanal–Wirkungsgrad $\eta_\text{K}$?}} | ||
| + | |||
| + | |||
| + | $\Rightarrow\hspace{0.3cm}\text{Es gilt }\vert H_{\rm E}(f = 0) \vert = \vert H_{\rm E}(f = 0) \vert ^{-1}= 1 \text{ und das Maximum von } \vert H_{\rm E}(f) \vert \text{ ist ca. }37500\text{ für }r=0.7 \Rightarrow 10 \cdot \lg \ \eta_\text{K+E} \approx -89.2 \ {\rm dB},$ | ||
| + | |||
| + | $\hspace{0.95cm}\text{weil das Intergral über }\vert H_{\rm E}(f) \vert^2\text{sehr groß ist. Nach Optimierung von }r=0.17 \text{ erhält man }10 \cdot \lg \ \eta_\text{K} \approx -82.6 \ {\rm dB}.$ | ||
| + | |||
| + | |||
| + | {{BlaueBox|TEXT= | ||
| + | '''(11)''' Es gelten die Einstellungen von '''(10) und $r= 0.17$. Variieren Sie die Kabellänge bis $l_{\rm blue} =10 \ \rm km$. | ||
| + | :Wie ändert sich der Maximalwert von $\vert H_{\rm E}(f) \vert$, der Kanal–Wirkungsgrad $\eta_\text{K}$ und der optimale Roll–off–Faktor $r_{\rm opt}$?}} | ||
| + | |||
| + | |||
| + | $\Rightarrow\hspace{0.3cm}\text{Der Maximalwert von } \vert H_{\rm E}(f) \vert \text{wird immer größer und }10 \cdot \lg \ \eta_\text{K}\text{ immer kleiner.}$ | ||
| + | |||
| + | $\hspace{0.95cm}\text{Bei 10 km Länge ist } 10 \cdot \lg \ \eta_\text{K} \approx -104.9 \ {\rm dB} \text{ und } r_{\rm opt}=0.14\text{. Für }f_\star \approx 14.5\ {\rm MHz} \text{ ist } \vert H_{\rm E}(f = f_\star) = 352000 \cdot \approx \vert H_{\rm E}(f =0)\vert$. | ||
| + | |||
| + | |||
| + | |||
| + | ==Zur Handhabung des Applets== | ||
| + | [[File:Applet_Kabeldaempfung_5_version2.png|left|600px]] | ||
| + | '''(A)''' Vorauswahl für blauen Parametersatz | ||
| + | |||
| + | '''(B)''' Eingabe der $\alpha$–Parameter per Slider | ||
| + | |||
| + | '''(C)''' Vorauswahl für roten Parametersatz | ||
| + | |||
| + | '''(D)''' Eingabe der $k$–Parameter per Slider | ||
| + | |||
| + | '''(E)''' Eingabe der Parameter $f_{\rm Nyq}$ und $r$ | ||
| + | |||
| + | '''(F)''' Auswahl für die graphische Darstellung | ||
| + | |||
| + | '''(G)''' Darstellung $a_\text{K}(f)$, $|H_\text{K}(f)|$, $|H_\text{E}(f)|$, ... | ||
| + | |||
| + | '''(H)''' Skalierungsfaktor $H_0$ für $|H_\text{E}(f)|$, $|H_\text{E}(f)|^2$ | ||
| + | |||
| + | '''(I)''' Auswahl der Frequenz $f_\star$ für Numerikausgabe | ||
| + | |||
| + | '''(J)''' Numerikausgabe für blauen Parametersatz | ||
| + | |||
| + | '''(K)''' Numerikausgabe für roten Parametersatz | ||
| + | |||
| + | '''(L)''' Ausgabe Systemwirkungsgrad $\eta_\text{K+E}$ in dB | ||
| + | |||
| + | '''(M)''' Store & Recall von Einstellungen | ||
| + | |||
| + | '''(N)''' Bereich für die Versuchsdurchführung | ||
| + | |||
| + | '''(O)''' Variation der grafischen Darstellung:$\hspace{0.5cm}$"$+$" (Vergrößern), | ||
| + | |||
| + | $\hspace{0.5cm}$ "$-$" (Verkleinern) | ||
| + | |||
| + | $\hspace{0.5cm}$ "$\rm o$" (Zurücksetzen) | ||
| + | $\hspace{0.5cm}$ "$\leftarrow$" (Verschieben nach links), usw. | ||
| + | '''Andere Möglichkeiten zur Variation der grafischen Darstellung''': | ||
| + | *Gedrückte Shifttaste und Scrollen: Zoomen im Koordinatensystem, | ||
| + | *Gedrückte Shifttaste und linke Maustaste: Verschieben des Koordinatensystems. | ||
| − | == | + | ==Über die Autoren== |
| + | Dieses interaktive Berechnungstool wurde am [http://www.lnt.ei.tum.de/startseite Lehrstuhl für Nachrichtentechnik] der [https://www.tum.de/ Technischen Universität München] konzipiert und realisiert. | ||
| + | *Die erste Version wurde 2009 von [[Biographies_and_Bibliographies/An_LNTwww_beteiligte_Studierende#Sebastian_Seitz_.28Diplomarbeit_LB_2009.29|Sebastian Seitz]] im Rahmen seiner Diplomarbeit erstellt (Betreuer: [[Biographies_and_Bibliographies/An_LNTwww_beteiligte_Mitarbeiter_und_Dozenten#Prof._Dr.-Ing._habil._G.C3.BCnter_S.C3.B6der_.28am_LNT_seit_1974.29|Günter Söder]] und [[Biographies_and_Bibliographies/Beteiligte_der_Professur_Leitungsgebundene_Übertragungstechnik#Dr.-Ing._Bernhard_G.C3.B6bel_.28bei_L.C3.9CT_von_2004-2010.29|Bernhard Göbel]]). | ||
| + | *2018 wurde das Programm von [[Biographies_and_Bibliographies/An_LNTwww_beteiligte_Studierende#Jimmy_He_.28Bachelorarbeit_2018.29|Jimmy He]] (Bachelorarbeit, Betreuer: [[Biographies_and_Bibliographies/Beteiligte_der_Professur_Leitungsgebundene_%C3%9Cbertragungstechnik#Tasn.C3.A1d_Kernetzky.2C_M.Sc._.28bei_L.C3.9CT_seit_2014.29|Tasnád Kernetzky]] ) auf "HTML5" umgesetzt und neu gestaltet. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | {{ | + | {{LntAppletLink|attenuationCopperCables_en}} |
Latest revision as of 15:46, 28 May 2021
Contents
Programmbeschreibung
Dieses Applet berechnet die Dämpfungsfunktion $a_{\rm K}(f)$ von leitungsgebundenen Übertragungsmedien (jeweils mit der Kabellänge $l$):
- Für Koaxialkabel verwendet man meist die Gleichung $a_{\rm K}(f)=(\alpha_0+\alpha_1\cdot f+\alpha_2\cdot \sqrt{f}) \cdot l$.
- Dagegen werden Zweidrahtleitungen oft in der Form $a_{\rm K}(f)=(k_1+k_2\cdot (f/{\rm MHz})^{k_3}) \cdot l$ dargestellt.
- Realisiert ist auch die Umrechnung der $(k_1, \ k_2, \ k_3)$–Darstellung in die $(\alpha_0, \ \alpha_1, \ \alpha_2)$–Form für $B = 30 \ \rm MHz$ und umgekehrt.
Außer der Dämpfungsfunktion $a_{\rm K}(f)$ können graphisch dargestellt werden:
- der zugehörige Betragsfrequenzgang $\left | H_{\rm K}(f)\right |=10^{-a_\text{K}(f)/20},$
- der Entzerrer–Frequenzgang $\left | H_{\rm E}(f)\right | = \left | H_{\rm CRO}(f) / H_{\rm K}(f)\right | $, der zu einem Nyquist–Gesamtfrequenzgang $ H_{\rm CRO}(f) $ führt,
- der entsprechende Betrags–Quadrat–Frequenzgang $\left | H_{\rm E}(f)\right |^2 $.
Das Integral über $\left | H_{\rm E}(f)\right |^2 $ ist ein Maß für die Rauschüberhöhung des ausgewählten Nyquist–Gesamtfrequenzgangs und damit auch für zu erwartende Fehlerwahrscheinlichkeit. Aus dieser wird der Gesamt–Wirkungsgrad $\eta_\text{K+E}$ für Kanal und Entzerrer berechnet, der im Applet in $\rm dB$ ausgegeben wird.
Durch Optimierung des Roll-off–Faktors $r$ des Cosinus–Roll-off–Frequenzgangs $ H_{\rm CRO}(f) $ kommt man zum Kanal–Wirkungsgrad $ \eta_\text{K}$. Dieser gibt also die Verschlechterung des Gesamtsystems aufgrund der Dämpfungsfunktion $a_{\rm K}(f)$ des Übertragungsmediums an.
Theoretischer Hintergrund
Betragsfrequenzgang und Dämpfungsfunktion
Es besteht folgender Zusammenhang zwischen dem Betragsfrequenzgang und der Dämpfungsfunktion:
- $$\left | H_{\rm K}(f)\right |=10^{-a_\text{K}(f)/20} = {\rm e}^{-a_\text{K, Np}(f)}.$$
- Der Index "K" soll deutlich machen, dass das betrachtete LZI–System ein Kabel ist.
- Bei der ersten Berechnungsvorschrift ist die Dämpfungsfunktion $a_\text{K}(f)$ in $\rm dB$ (Dezibel) einzusetzen.
- Bei der zweiten Berechnungsvorschrift ist die Dämpfungsfunktion $a_\text{K, Np}(f)$ in $\rm Np$ (Neper) einzusetzen.
- Es gelten folgende Umrechnungen $\rm 1 \ dB = 0.05 \cdot \ln (10) \ Np= 0.1151 \ Np$ bzw. $\rm 1 \ Np = 20 \cdot \lg (e) \ dB= 8.6859 \ dB$.
- In diesem Applet werden ausschließlich die dB–Werte verwendet.
Dämpfungsfunktion eines Koaxialkabels
Die Dämpfungsfunktion eines Koaxialkabels der Länge $l$ wird in [Wel77][1] wie folgt angegeben:
- $$a_{\rm K}(f)=(\alpha_0+\alpha_1\cdot f+\alpha_2\cdot \sqrt{f}) \cdot l.$$
- Beachten Sie bitte den Unterschied zwischen der Dämpfungsfunktion $a_{\rm K}(f)$ in $\rm dB$ und den "alpha"–Koeffizienten $\alpha_{\rm K}(f)=a_{\rm K}(f)/l$ mit anderen Pseudo–Einheiten.
- Die Dämpfungsfunktion $a_{\rm K}(f)$ ist direkt proportional zur Kabellänge $l$. Man bezeichnet den Quotienten $a_{\rm K}(f)/l$ als "Dämpfungsmaß" oder "kilometrische Dämpfung".
- Der frequenzunabhängige Anteil $α_0$ des Dämpfungsmaßes berücksichtigt die Ohmschen Verluste ("Leitungsverluste").
- Der frequenzproportionale Anteil $α_1 · f$ des Dämpfungsmaßes ist auf die Ableitungsverluste ("Querverluste") zurückzuführen.
- Der dominante Anteil $α_2$ geht auf den Skineffekt zurück, der bewirkt, dass bei höherfrequentem Wechselstrom die Stromdichte im Leiterinneren niedriger ist als an der Oberfläche. Dadurch steigt der Widerstandsbelag einer elektrischen Leitung mit der Wurzel aus der Frequenz an.
Die Konstanten für das Normalkoaxialkabel mit 2.6 mm Innendurchmesser und 9.5 mm Außendurchmesser ⇒ kurz Coax (2.6/9.5 mm) lauten:
- $$\alpha_0 = 0.014\, \frac{ {\rm dB} }{ {\rm km} }\hspace{0.05cm}, \hspace{0.2cm} \alpha_1 = 0.0038\, \frac{ {\rm dB} }{ {\rm km \cdot MHz} }\hspace{0.05cm}, \hspace{0.2cm} \alpha_2 = 2.36\, \frac{ {\rm dB} }{ {\rm km \cdot \sqrt{MHz} } }\hspace{0.05cm}.$$
Entsprechend gilt für das Kleinkoaxialkabel ⇒ kurz Coax (1.2/4.4 mm):
- $$\alpha_0 = 0.068\, \frac{ {\rm dB} }{ {\rm km} }\hspace{0.05cm}, \hspace{0.2cm} \alpha_1 = 0.0039\, \frac{ {\rm dB} }{ {\rm km \cdot MHz} }\hspace{0.05cm}, \hspace{0.2cm} \alpha_2 =5.2\, \frac{ {\rm dB} }{ {\rm km \cdot \sqrt{MHz} } }\hspace{0.05cm}.$$
Diese Werte können aus den geometrischen Abmessungen der Kabel berechnet werden und wurden durch Messungen am Fernmeldetechnischen Zentralamt in Darmstadt bestätigt – siehe [Wel77][1] . Sie gelten für eine Temperatur von 20°C (293 K) und Frequenzen größer als 200 kHz.
Dämpfungsfunktion einer Zweidrahtleitung
Die Dämpfungsfunktion einer Zweidrahtleitung (englisch: Two–wired Line) der Länge $l$ wird in [PW95][2] wie folgt angegeben:
- $$a_{\rm K}(f)=(k_1+k_2\cdot (f/{\rm MHz})^{k_3}) \cdot l.$$
Dieser Funktionsverlauf ist nicht direkt interpretierbar, sondern es handelt sich um eine phänomenologische Beschreibungsform.
Ebenfalls in [PW95][2]findet man die aus Messergebnissen ermittelten Konstanten für verschiedene Leitungsdurchmesser $d$:
- $d = 0.35 \ {\rm mm}$: $k_1 = 7.9 \ {\rm dB/km}, \hspace{0.2cm}k_2 = 15.1 \ {\rm dB/km}, \hspace{0.2cm}k_3 = 0.62$,
- $d = 0.40 \ {\rm mm}$: $k_1 = 5.1 \ {\rm dB/km}, \hspace{0.2cm}k_2 = 14.3 \ {\rm dB/km}, \hspace{0.2cm}k_3 = 0.59$,
- $d = 0.50 \ {\rm mm}$: $k_1 = 4.4 \ {\rm dB/km}, \hspace{0.2cm}k_2 = 10.8 \ {\rm dB/km}, \hspace{0.2cm}k_3 = 0.60$,
- $d = 0.60 \ {\rm mm}$: $k_1 = 3.8 \ {\rm dB/km}, \hspace{0.2cm}k_2 = \hspace{0.25cm}9.2 \ {\rm dB/km}, \hspace{0.2cm}k_3 = 0.61$.
Man erkennt aus diesen Zahlenwerten:
- Dämpfungsmaß $α(f)$ und Dämpfungsfunktion $a_{\rm K}(f) = α(f) · l$ hängen signifikant vom Leitungsdurchmesser ab. Die seit 1994 verlegten Kabel mit $d = 0.35$ mm und $d = 0.5$ mm haben etwa ein um $10\%$ größeres Dämpfungsmaß als die älteren Leitungen mit $d = 0.4$bzw. $0.6$ mm.
- Dieser mit den Herstellungs– und Verlegungskosten begründete kleinere Durchmesser vermindert allerdings die Reichweite $l_{\rm max}$ der auf diesen Leitungen eingesetzten Übertragungssysteme signifikant, so dass im schlimmsten Fall teuere Zwischenregeneratoren eingesetzt werden müssen.
- Die heute üblichen Übertragungsverfahren für Kupferleitungen belegen allerdings nur ein relativ schmales Frequenzband, zum Beispiel sind dies bei ISDN $120\ \rm kHz$ und bei DSL ca. $1100 \ \rm kHz$. Für $f = 1 \ \rm MHz$ beträgt das Dämpfungsmaß für ein 0.4 mm–Kabel etwa $20 \ \rm dB/km$, so dass selbst bei einer Kabellänge von $l = 4 \ \rm km$ der Dämpfungswert nicht über $80 \ \rm dB$ liegt.
Umrechnung zwischen $k$– und $\alpha$– Parametern
Es besteht die Möglichkeit, die $k$–Parameter des Dämpfungsmaßes ⇒ $\alpha_{\rm I} (f)$ in entsprechende $\alpha$–Parameter ⇒ $\alpha_{\rm II} (f)$ umzurechnen:
- $$\alpha_{\rm I} (f) = k_1 + k_2 \cdot (f/f_0)^{k_3}\hspace{0.05cm}, \hspace{0.2cm}{\rm mit} \hspace{0.15cm} f_0 = 1\,{\rm MHz},$$
- $$\alpha_{\rm II} (f) = \alpha_0 + \alpha_1 \cdot f + \alpha_2 \cdot \sqrt {f}.$$
Als Kriterium dieser Umrechnung gehen wir davon aus, dass die quadratische Abweichung dieser beiden Funktionen innerhalb einer Bandbreite $B$ minimal ist:
- $$\int_{0}^{B} \left [ \alpha_{\rm I} (f) - \alpha_{\rm II} (f)\right ]^2 \hspace{0.1cm}{\rm d}f \hspace{0.3cm}\Rightarrow \hspace{0.3cm}{\rm Minimum} \hspace{0.05cm} .$$
Es ist offensichtlich, dass $α_0 = k_1$ gelten wird. Die Parameter $α_1$ und $α_2$ sind von der zugrundegelegten Bandbreite $B$ abhängig und lauten:
- $$\begin{align*}\alpha_1 & = 15 \cdot (B/f_0)^{k_3 -1}\cdot \frac{k_3 -0.5}{(k_3 + 1.5)(k_3 + 2)}\cdot {k_2}/{ {f_0} }\hspace{0.05cm} ,\\ \alpha_2 & = 10 \cdot (B/f_0)^{k_3 -0.5}\cdot \frac{1-k_3}{(k_3 + 1.5)(k_3 + 2)}\cdot {k_2}/{\sqrt{f_0} }\hspace{0.05cm} .\end{align*}$$
In der Gegenrichtung lautet die Umrechnungsvorschrift für den Exponenten:
- $$k_3 = \frac{A + 0.5} {A +1}, \hspace{0.2cm}\text{Hilfsgröße: }A = \frac{2} {3} \cdot \frac{\alpha_1 \cdot \sqrt{f_0}}{\alpha_2} \cdot \sqrt{B/f_0}.$$
Mit diesem Ergebnis lässt sich $k_2$ mit jeder der oberen Gleichungen angeben.
$\text{Beispiel 1:}$ Im Folgenden verwenden wir die Normierunggröße $f_0 = 1 \ \rm MHz$.
- Für $k_3 = 1$ (frequenzproportionales Dämpfungsmaß) ergeben sich folgerichtig $\alpha_0 = k_0\hspace{0.05cm} ,\hspace{0.2cm} \alpha_1 = {k_2}/{ {f_0} }\hspace{0.05cm} ,\hspace{0.2cm} \alpha_2 = 0\hspace{0.05cm} .$
- Für $k_3 = 0.5$ (entsprechend Skineffekt) erhält man folgende Koeffizienten: $\alpha_0 = k_0\hspace{0.05cm} ,\hspace{0.2cm}\alpha_1 = 0\hspace{0.05cm} ,\hspace{0.2cm} \alpha_2 = {k_2}/{\sqrt{f_0} }\hspace{0.05cm}.$
- Für $k_3 < 0.5$ ergibt sich ein negatives $\alpha_1$. Umrechnung ist nur für $0.5 \le k_3 \le 1$ möglich.
- Für $0.5 \le k_3 \le$ ergeben sich Koeffizienten $\alpha_1 > 0$ und $\alpha_2 > 0$, die auch von $B/f_0$ abhängen.
- Aus $\alpha_1 = 0.3\, {\rm dB}/ ({\rm km \cdot MHz}) \hspace{0.05cm}, \hspace{0.2cm} \alpha_2 = 3\, {\rm dB}/ ({\rm km \cdot \sqrt{MHz} })\hspace{0.05cm},\hspace{0.2cm}B = 30 \ \rm MHz$ folgt $k_3 = 0.63$ und $k_2 = 2.9 \ \rm dB/km$.
Zum Kanaleinfluss auf die binäre Nyquistentzerrung
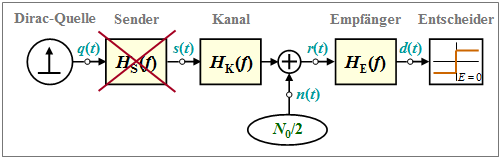
Wir gehen vom skizzierten Blockschaltbild aus. Zwischen der Diracquelle und dem Entscheider liegen die Frequenzgänge für Sender ⇒ $H_{\rm S}(f)$, Kanal ⇒ $H_{\rm K}(f)$ und Empfänger ⇒ $H_{\rm E}(f)$.
In diesem Applet
- vernachlässigen wir den Einfluss der Sendeimpulsform ⇒ $H_{\rm S}(f) \equiv 1$ ⇒ diracförmiges Sendesignal $s(t)$,
- setzen ein binäres Nyquistsystem mit Cosinus–Roll-off um die Nyquistfrequenz $f_{\rm Nyq} = [f_1 + f_2]/2 =1(2T)$ voraus:
- $$H_{\rm K}(f) · H_{\rm E}(f) = H_{\rm CRO}(f).$$
Das bedeutet: Das erste Nyquistkriterium wird erfüllt ⇒ zeitlich aufeinander folgende Impulse stören sich nicht gegenseitig ⇒ es gibt keine Impulsinterferenzen (englisch: Intersymbol Interference, ISI).
Bei weißem Rauschen wird somit die Übertragungsqualität allein durch die Rauschleistung vor dem Empfänger bestimmt:
- $$P_{\rm N} =\frac{N_0}{2} \cdot \int_{-\infty}^{+\infty} |H_{\rm E}(f)|^2 \ {\rm d}f\hspace{1cm}\text{mit}\hspace{1cm}|H_{\rm E}(f)|^2 = \frac{|H_{\rm CRO}(f)|^2}{|H_{\rm K}(f)|^2}.$$
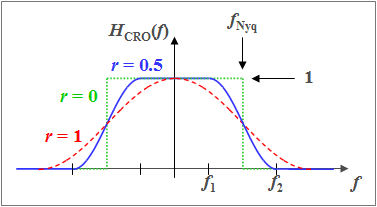
Die kleinstmögliche Rauschleistung ergibt sich bei idealem Kanal ⇒ $H_{\rm K}(f) \equiv 1$ und gleichzeitig dem Frequenzgang $H_{\rm CRO}(f)$ mit Roll-off–Faktor $r = 1$ im Bereich $|f| \le 2 \cdot f_{\rm Nyq}$ (siehe Skizze):
- $$P_\text{N, min} = P_{\rm N} \ \big [\text{optimales System: }H_{\rm K}(f) \equiv 1; \ \text{ Roll-off–Faktor } r=r_{\rm opt} =1 \big ] = N_0 \cdot 3/4 \cdot f_{\rm Nyq} .$$
$\text{Definitionen:}$
- Als Gütekriterium für ein gegebenes System verwenden wir den Gesamt–Wirkungsgrad:
- $$\eta_\text{K+E} = \frac{P_{\rm N} \ \big [\text{optimales System: }H_{\rm K}(f) \equiv 1, \ r=r_{\rm opt} =1 \big ]}{P_{\rm N} \ \big [\text{gegebenes System: Kanal }H_{\rm K}(f), \ \text{Roll-off-Faktor }r \big ]} =\left [ \frac{1}{3/4 \cdot f_{\rm Nyq} } \cdot \int_{0}^{+\infty} \vert H_{\rm E}(f) \vert^2 \ {\rm d}f \right ]^{-1}\le 1.$$
- Diese Systemgröße wird im Applet für beide Parametersätze in logarithmierter Form angegeben: $10 \cdot \lg \ \eta_\text{K+E} \le 0 \ \rm dB$.
- Durch Variation und Optimierung des Roll-off-Faktors $r$ erhält man den Kanal–Wirkungsgrad:
- $$\eta_\text{K} = \max_{0 \le r \le 1} \ \eta_\text{K+E} .$$
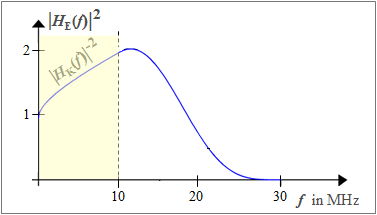
$\text{Beispiel 2:}$ Die Grafik zeigt den Betrags–Quadrat–Frequenzgang $\left \vert H_{\rm E}(f)\right \vert ^2 $ mit $\left \vert H_{\rm E}(f)\right \vert = H_{\rm CRO}(f) / \left \vert H_{\rm K}(f)\right \vert$ für folgende Randbedingungen:
- Dämpfungsfunktion des Kanals: $a_{\rm K}(f) = 1 \ {\rm dB} \cdot \sqrt{f/\ {\rm MHz} }$,
- Nyquist–Frequenz: : $f_{\rm Nyq} = 20 \ {\rm MHz}$, Roll-off-Faktor $r = 0.5$
Daraus ergeben sich folgende Konsequenzen:
- Im Bereich bis $f_{1} = 10 \ {\rm MHz}$ ist $H_{\rm CRO}(f) = 1$ ⇒ $\left \vert H_{\rm E}(f)\right \vert ^2 = \left \vert H_{\rm K}(f)\right \vert ^{-2}$ (siehe gelbe Hinterlegung).
- Erst im Bereich von $f_{1}$ bis $f_{2} = 30 \ {\rm MHz}$ ist die Flanke von $H_{\rm CRO}(f)$ wirksam und $\left \vert H_{\rm E}(f)\right \vert ^2$ wird immer kleiner.
- Das Maximum von $\left \vert H_{\rm E}(f_{\rm max})\right \vert ^2$ bei $f_{\rm max} \approx 11.5 \ {\rm MHz}$ ist mehr als doppelt so groß wie $\left \vert H_{\rm E}(f = 0)\right \vert ^2 = 1$.
- Das Integral über $\left \vert H_{\rm E}(f)\right \vert ^2$ ist ein Maß für die wirksame Rauschleistung. Diese ist im Beispiel um den Faktor $4.6$ größer als die minimale Rauschleistung (für $a_{\rm K}(f) = 0 \ {\rm dB}$ und $r=1$) ⇒ $10 \cdot \lg \ \eta_\text{K+E} \approx - 6.6 \ {\rm dB}.$
Versuchsdurchführung
- Wählen Sie zunächst die Nummer 1 ... 11 der zu bearbeitenden Aufgabe.
- Der Aufgabentext wird angezeigt. Die Parameterwerte sind angepasst.
- Lösung nach Drücken von "Hide solution".
- Aufgabenstellung und Lösung in Englisch.
Die Nummer 0 entspricht einem "Reset":
- Gleiche Einstellung wie beim Programmstart.
- Ausgabe eines "Reset–Textes" mit weiteren Erläuterungen zum Applet.
In der folgenden Beschreibung bezeichnet Blue den linken Parametersatz (im Applet blau markiert) Red den rechten Parametersatz (im Applet rot markiert). Alle Angaben mit Hochkomma sind ohne Einheit, zum Beispiel steht ${\alpha_2}' =2$ für $\alpha_2 =2\, {\rm dB} / ({\rm km \cdot \sqrt{MHz} })$.
(1) Setzen Sie Blue zunächst auf $\text{Coax (1.2/4.4 mm)}$ und anschließend auf $\text{Coax (2.6/9.5 mm)}$. Die Kabellänge sei jeweils $l_{\rm Blue}= 5\ \rm km$.
- Betrachten und Interpretieren Sie $a_{\rm K}(f)$ und $\vert H_{\rm K}(f) \vert$, insbesondere die Funktionswerte $a_{\rm K}(f = f_\star = 30 \ \rm MHz)$ und $\vert H_{\rm K}(f = 0) \vert$.
$\Rightarrow\hspace{0.3cm}\text{Näherungsweise steigt die Dämpfungsfunktion mit }\sqrt{f}\text{ und der Betragsfrequenzgang fällt ähnlich einer Exponentialfunktion};$
$\hspace{1.15cm}\text{Coax (1.2/4.4 mm): }a_{\rm K}(f = f_\star) = 143.3\text{ dB;}\hspace{0.5cm}\vert H_{\rm K}(f = 0) \vert = 0.96.$
$\hspace{1.15cm}\text{Coax (2.6/9.5 mm): }a_{\rm K}(f = f_\star) = 65.3\text{ dB;}\hspace{0.5cm}\vert H_{\rm K}(f = 0) \vert = 0.99;$
(2) Für Blue gelte $\text{Coax (2.6/9.5 mm)}$ und $l_{\rm Blue} = 5\ \rm km$. Wie wird $a_{\rm K}(f =f_\star = 30 \ \rm MHz)$ von $\alpha_0$, $\alpha_1$ und $\alpha_2$ beeinflusst?
$\Rightarrow\hspace{0.3cm}\text{Entscheidend ist }\alpha_2\text{ (Skineffekt). Die Beitrag von } \alpha_0\text{ ist nur ca. 0.1 dB und der von }\alpha_1 \text{ nur ca. 0.6 dB.}$
(3) Setzen Sie zusätzlich Red auf $\text{Two–wired Line (0.5 mm)}$ und $l_{\rm Red} = 1\ \rm km$. Welcher Wert ergibt sich für $a_{\rm K}(f =f_\star= 30 \ \rm MHz)$?
- Bis zu welcher Länge $l_{\rm Red}$ ist die rote Dämpfungsfunktion vergleichbar mit der blauen?
$\Rightarrow\hspace{0.3cm}\text{Für die rote Kurve gilt: }a_{\rm K}(f = f_\star) = 87.5 {\ \rm dB} \text{. Obige Bedingung wird erfüllt für }l_{\rm Red} = 0.7\ {\rm km} \ \Rightarrow \ a_{\rm K}(f = f_\star) = 61.3 {\ \rm dB}.$
(4) Setzen Sie Red auf ${k_1}' = 0, {k_2}' = 10, {k_3}' = 0.75, {l_{\rm red} } = 1 \ \rm km$ und variieren Sie den Parameter $0.5 \le k_3 \le 1$.
- Was erkennt man anhand von $a_{\rm K}(f)$ und $\vert H_{\rm K}(f) \vert$?
$\Rightarrow\hspace{0.3cm}\text{Bei festem }k_2\text {wird }a_{\rm K}(f)\text{ mit größerem }k_3\text{ immer größer und }\vert H_{\rm K}(f) \vert \text{ nimmt immer schneller ab. Mit }k_3 =1: a_{\rm K}(f)\text{ steigt linear.}$
$\hspace{1.15cm}\text{Mit }k_3 \to 0.5\text{ wird die Dämpfungsfunktion wie beim Koaxialkabel immer mehr durch den Skineffekt bestimmt.}$
(5) Setzen Sie Red auf $\text{Two–wired Line (0.5 mm)}$ und Blue auf $\text{Conversion of Red}$. Es gelte $l_{\rm Red} = l_{\rm Blue} = 1\ \rm km$.
- Betrachten und interpretieren Sie die dargestellten Funktionsverläufe für $a_{\rm K}(f)$ und $\vert H_{\rm K}(f) \vert$.
$\Rightarrow\hspace{0.3cm}\text{Sehr gute Approximation der Zweidrahtleitung durch den blauen Parametersatz, sowohl bezüglich }a_{\rm K}(f) \text{ als auch }\vert H_{\rm K}(f) \vert.$
$\hspace{1.15cm}\text{Die errechneten Parameterwerte nach der Konvertierung sind }{\alpha_0}' = {k_1}' = 4.4, \ {\alpha_1}' = 0.76, \ {\alpha_2}' = 11.12.$
(6) Es gelten die Einstellungen von (5). Welche Anteile der Dämpfungsfunktion gehen auf Ohmschen Verlust, Querverluste und Skineffekt zurück?
$\Rightarrow\hspace{0.3cm}\text{Lösung anhand '''Blue''': }a_{\rm K}(f = f_\star= 30 \ {\rm MHz}) = 88.1\ {\rm dB}, \hspace{0.2cm}\text{ohne }\alpha_0\text{: }83.7\ {\rm dB}, \hspace{0.2cm}\text{ohne }\alpha_0 \text{ und } \alpha_1\text{: }60.9\ {\rm dB}.$
$\hspace{1.15cm}\text{Bei einer Zweidrahtleitung ist der Einfluss der Längs– und der Querverluste signifikant größer als bei einem Koaxialkabel.}$
(7) Setzen Sie Blue auf ${\alpha_0}' = {\alpha_1}' ={\alpha_2}' = 0$ und Red auf ${k_1}' = 2, {k_2}' = 0, {l_{\rm red} } = 1 \ \rm km$. Zusätzlich gelte ${f_{\rm Nyq} }' =15$ und $r= 0.5$.
- Wie groß ist jeweils der Gesamt–Wirkungsgrad $\eta_\text{K+E}$ und der Kanal–Wirkungsgrad $\eta_\text{K}$?
$\Rightarrow\hspace{0.3cm}\text{Es gilt }10 \cdot \lg \ \eta_\text{K+E} = -0.7\ \ {\rm dB}\text{ (Blue: ideales System) und }10 \cdot \lg \ \eta_\text{K+E} = -2.7\ \ {\rm dB}\text{ (Red: nur Gleichsignaldämpfung)}$.
$\hspace{0.95cm}\text{Der bestmögliche Rolloff–Faktor ist }r = 1.\text{ Somit ist }10 \cdot \lg \ \eta_\text{K} = 0 \ {\rm dB}\text{ (Blue) bzw. }10 \cdot \lg \ \eta_\text{K} = -2\ {\rm dB}\text{ (Red)}.$
(8) Es gilt die Einstellung von (7). Mit welcher Sendeleistung $P_{\rm red}$ in Bezug zu $P_{\rm blue}$ erreichen beide Systeme gleiche Fehlerwahrscheinlichkeit?
$\Rightarrow\hspace{0.3cm}\text{Es muss gelten: }10 \cdot \lg \ P_{\rm red}/P_{\rm blue} =2 \ {\rm dB} \ \ \text{ ⇒ } \ \ P_{\rm red}/P_{\rm blue} = 10^{0.2} = 1.585.$
(9) Setzen Sie Blue auf ${\alpha_0}' = {\alpha_1}' = 0, \ {\alpha_2}' = 3, \ {l_{\rm blue} }' = 2$ und Red auf "Inactive". Zusätzlich gelte ${f_{\rm Nyq} }' =15$ und $r= 0.7$.
- Welchen Verlauf hat $\vert H_{\rm E}(f) \vert$? Wie groß ist sind Gesamt–Wirkungsgrad $\eta_\text{K+E}$ und Kanal–Wirkungsgrad $\eta_\text{K}$?
$\Rightarrow\hspace{0.3cm}\text{Für } f < 7.5 {\ \rm MHz}\text{ ist } \vert H_{\rm E}(f) \vert = \vert H_{\rm K}(f) \vert ^{-1}.\text{ Für }(f > 22.5 {\ \rm MHz)}\text{ ist: }\vert H_{\rm E}(f) \vert = 0.\text{ Dazwischen Einfluss der CRO–Flanke.}$
$\hspace{0.95cm}\text{Der bestmögliche Rolloff–Faktor }r = 0.7\text{ ist bereits eingestellt: }\Rightarrow \ 10 \cdot \lg \ \eta_\text{K+E} = 10 \cdot \lg \ \eta_\text{K} \approx - 18.1 \ {\rm dB}.$
(10) Setzen Sie Blue auf ${\alpha_0}' = {\alpha_1}' = 0, \ {\alpha_2}' = 3, \ {l_{\rm blue} }' = 8$ sowie Red auf "Inactive". Zusätzlich gelte ${f_{\rm Nyq} }' =15$ und $r= 0.7$.
- Welchen Wert hat $\vert H_{\rm E}(f = 0) \vert$? Was ist der Maximalwert von $\vert H_{\rm E}(f) \vert$? Wie groß ist ist der Kanal–Wirkungsgrad $\eta_\text{K}$?
$\Rightarrow\hspace{0.3cm}\text{Es gilt }\vert H_{\rm E}(f = 0) \vert = \vert H_{\rm E}(f = 0) \vert ^{-1}= 1 \text{ und das Maximum von } \vert H_{\rm E}(f) \vert \text{ ist ca. }37500\text{ für }r=0.7 \Rightarrow 10 \cdot \lg \ \eta_\text{K+E} \approx -89.2 \ {\rm dB},$
$\hspace{0.95cm}\text{weil das Intergral über }\vert H_{\rm E}(f) \vert^2\text{sehr groß ist. Nach Optimierung von }r=0.17 \text{ erhält man }10 \cdot \lg \ \eta_\text{K} \approx -82.6 \ {\rm dB}.$
(11) Es gelten die Einstellungen von (10) und $r= 0.17$. Variieren Sie die Kabellänge bis $l_{\rm blue} =10 \ \rm km$.
- Wie ändert sich der Maximalwert von $\vert H_{\rm E}(f) \vert$, der Kanal–Wirkungsgrad $\eta_\text{K}$ und der optimale Roll–off–Faktor $r_{\rm opt}$?
$\Rightarrow\hspace{0.3cm}\text{Der Maximalwert von } \vert H_{\rm E}(f) \vert \text{wird immer größer und }10 \cdot \lg \ \eta_\text{K}\text{ immer kleiner.}$
$\hspace{0.95cm}\text{Bei 10 km Länge ist } 10 \cdot \lg \ \eta_\text{K} \approx -104.9 \ {\rm dB} \text{ und } r_{\rm opt}=0.14\text{. Für }f_\star \approx 14.5\ {\rm MHz} \text{ ist } \vert H_{\rm E}(f = f_\star) = 352000 \cdot \approx \vert H_{\rm E}(f =0)\vert$.
Zur Handhabung des Applets
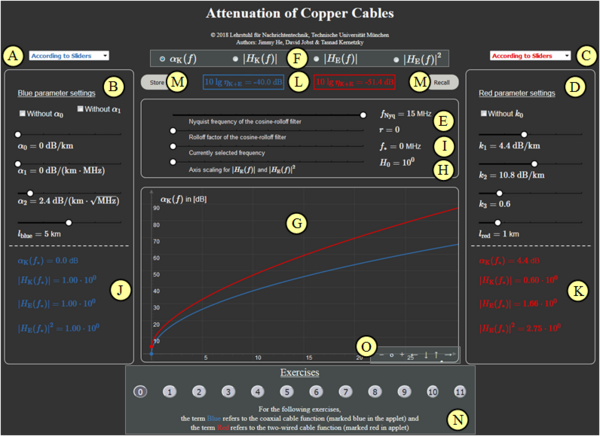
(A) Vorauswahl für blauen Parametersatz
(B) Eingabe der $\alpha$–Parameter per Slider
(C) Vorauswahl für roten Parametersatz
(D) Eingabe der $k$–Parameter per Slider
(E) Eingabe der Parameter $f_{\rm Nyq}$ und $r$
(F) Auswahl für die graphische Darstellung
(G) Darstellung $a_\text{K}(f)$, $|H_\text{K}(f)|$, $|H_\text{E}(f)|$, ...
(H) Skalierungsfaktor $H_0$ für $|H_\text{E}(f)|$, $|H_\text{E}(f)|^2$
(I) Auswahl der Frequenz $f_\star$ für Numerikausgabe
(J) Numerikausgabe für blauen Parametersatz
(K) Numerikausgabe für roten Parametersatz
(L) Ausgabe Systemwirkungsgrad $\eta_\text{K+E}$ in dB
(M) Store & Recall von Einstellungen
(N) Bereich für die Versuchsdurchführung
(O) Variation der grafischen Darstellung:$\hspace{0.5cm}$"$+$" (Vergrößern), $\hspace{0.5cm}$ "$-$" (Verkleinern) $\hspace{0.5cm}$ "$\rm o$" (Zurücksetzen) $\hspace{0.5cm}$ "$\leftarrow$" (Verschieben nach links), usw.
Andere Möglichkeiten zur Variation der grafischen Darstellung:
- Gedrückte Shifttaste und Scrollen: Zoomen im Koordinatensystem,
- Gedrückte Shifttaste und linke Maustaste: Verschieben des Koordinatensystems.
Über die Autoren
Dieses interaktive Berechnungstool wurde am Lehrstuhl für Nachrichtentechnik der Technischen Universität München konzipiert und realisiert.
- Die erste Version wurde 2009 von Sebastian Seitz im Rahmen seiner Diplomarbeit erstellt (Betreuer: Günter Söder und Bernhard Göbel).
- 2018 wurde das Programm von Jimmy He (Bachelorarbeit, Betreuer: Tasnád Kernetzky ) auf "HTML5" umgesetzt und neu gestaltet.
- ↑ 1.0 1.1 Wellhausen, H. W.: Dämpfung, Phase und Laufzeiten bei Weitverkehrs–Koaxialpaaren. Frequenz 31, S. 23-28, 1977.
- ↑ 2.0 2.1 Pollakowski, M.; Wellhausen, H.W.: Eigenschaften symmetrischer Ortsanschlusskabel im Frequenzbereich bis 30 MHz. Mitteilung aus dem Forschungs- und Technologiezentrum der Deutschen Telekom AG, Darmstadt, Verlag für Wissenschaft und Leben Georg Heidecker, 1995.