Difference between revisions of "Applets:Zur Erzeugung von Walsh-Funktionen (neues Applet)"
m (Text replacement - "„" to """) |
|||
| (10 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{LntAppletLink| | + | {{LntAppletLink|walsh}} |
| Line 6: | Line 6: | ||
==Programmbeschreibung== | ==Programmbeschreibung== | ||
<br> | <br> | ||
| − | Dieses Applet ermöglicht die Darstellung der Hadamard-Matrizen $\mathbf{H}_J$ zur Konstruktion der Walsh-Funktionen $w_j$. Dabei können der Faktor $J$ der Bandspreizung sowie die Markierung der einzelnen Walsh-Funktionen (durch blaue Umrandung der Zeilen der Matrix) verändert werden. | + | Dieses Applet ermöglicht die Darstellung der Hadamard-Matrizen $\mathbf{H}_J$ zur Konstruktion der Walsh-Funktionen $w_j$. Dabei können der Faktor $J$ der Bandspreizung sowie die Markierung der einzelnen Walsh-Funktionen (durch blaue Umrandung der Zeilen der Matrix) verändert werden. |
==Theoretischer Hintergrund== | ==Theoretischer Hintergrund== | ||
| Line 12: | Line 12: | ||
===Anwendung=== | ===Anwendung=== | ||
<br> | <br> | ||
| − | Die '''Walsh-Funktionen''' sind eine Gruppe von periodischen orthogonalen Funktionen. Ihr Anwendungsbereich in der digitalen Signalverarbeitung liegt vor allem in der Verwendung zur Bandspreizung bei CDMA-Systemen, beispielsweise dem Mobilfunkstandard UMTS. | + | Die '''Walsh-Funktionen''' sind eine Gruppe von periodischen orthogonalen Funktionen. Ihr Anwendungsbereich in der digitalen Signalverarbeitung liegt vor allem in der Verwendung zur Bandspreizung bei CDMA-Systemen, beispielsweise dem Mobilfunkstandard UMTS. |
*Aufgrund ihrer Orthogonalitätseigenschaften und der günstigen PKKF-Bedingungen (periodische KKF) stellen die Walsh-Funktionen für einen verzerrungsfreien Kanal und ein synchrones CDMA-System optimale Spreizfolgen dar. Nimmt man zwei beliebige Zeilen und bildet die Korrelation (Mittelung über die Produkte), so ergibt sich stets der PKKF–Wert Null. | *Aufgrund ihrer Orthogonalitätseigenschaften und der günstigen PKKF-Bedingungen (periodische KKF) stellen die Walsh-Funktionen für einen verzerrungsfreien Kanal und ein synchrones CDMA-System optimale Spreizfolgen dar. Nimmt man zwei beliebige Zeilen und bildet die Korrelation (Mittelung über die Produkte), so ergibt sich stets der PKKF–Wert Null. | ||
*Bei asynchronem Betrieb (Beispiel: Uplink eines Mobilfunksystems) oder De–Orthogonalisierung aufgrund von Mehrwegeausbreitung sind dagegen Walsh–Funktionen allein zur Bandspreizung nicht unbedingt geeignet – siehe [[Aufgaben:5.4_Walsh–Funktionen_(PKKF,_PAKF)|Aufgabe 5.4]]. | *Bei asynchronem Betrieb (Beispiel: Uplink eines Mobilfunksystems) oder De–Orthogonalisierung aufgrund von Mehrwegeausbreitung sind dagegen Walsh–Funktionen allein zur Bandspreizung nicht unbedingt geeignet – siehe [[Aufgaben:5.4_Walsh–Funktionen_(PKKF,_PAKF)|Aufgabe 5.4]]. | ||
| Line 20: | Line 20: | ||
===Konstruktion=== | ===Konstruktion=== | ||
<br> | <br> | ||
| − | Die Konstruktion der Walsh-Funktionen kann rekursiv mithilfe der '''Hadamard-Matrizen''' erfolgen. Eine Hadamard-Matrix $\mathbf{H}_J$ der Ordnung $J$ ist eine $J\times J$-Matrix, die zeilenweise die $\pm 1$-Gewichte der Walsh-Folgen enthält. Die Ordnungen der Hadamard-Matrizen sind dabei auf Zweierpotenzen festgelegt, d.h. es gilt $J = 2^G$ für eine natürliche Zahl $G$. Ausgehend von $\mathbf{H}_1 = | + | Die Konstruktion der Walsh-Funktionen kann rekursiv mithilfe der '''Hadamard-Matrizen''' erfolgen. Eine Hadamard-Matrix $\mathbf{H}_J$ der Ordnung $J$ ist eine $J\times J$-Matrix, die zeilenweise die $\pm 1$-Gewichte der Walsh-Folgen enthält. Die Ordnungen der Hadamard-Matrizen sind dabei auf Zweierpotenzen festgelegt, d.h. es gilt $J = 2^G$ für eine natürliche Zahl $G$. Ausgehend von $\mathbf{H}_1 = [+1]$ und |
| − | + | :$$ | |
\mathbf{H}_2 = | \mathbf{H}_2 = | ||
| − | \left | + | \left[ \begin{array}{rr} |
+1 & +1\\ | +1 & +1\\ | ||
+1 & -1 \\ | +1 & -1 \\ | ||
| − | \end{array}\right | + | \end{array}\right] |
| − | + | $$ | |
gilt der folgende Zusammenhang zur Generierung weiterer Hadamard-Matrizen: | gilt der folgende Zusammenhang zur Generierung weiterer Hadamard-Matrizen: | ||
| − | + | :$$ | |
\mathbf{H}_{2N} = | \mathbf{H}_{2N} = | ||
| − | \left | + | \left[ \begin{array}{rr} |
+\mathbf{H}_N & +\mathbf{H}_N\\ | +\mathbf{H}_N & +\mathbf{H}_N\\ | ||
+\mathbf{H}_N & -\mathbf{H}_N \\ | +\mathbf{H}_N & -\mathbf{H}_N \\ | ||
| − | \end{array}\right | + | \end{array}\right] |
| − | + | $$ | |
<br> | <br> | ||
| − | + | {{GraueBox|TEXT= | |
| − | + | $\text{Beispiel:}$ Die Grafik zeigt die Hadamard–Matrix $\mathbf H_8$ (rechts) und die damit $J -1$ konstruierbaren Spreizfolgen. | |
| − | Die Grafik zeigt die Hadamard–Matrix $\mathbf H_8$ (rechts) und die damit $J -1$ konstruierbaren Spreizfolgen. | + | [[File:P_ID1882__Mod_T_5_3_S7_neu.png|right|frame| Walsh–Spreizfolgen $(J = 8)$ und Hadamard–Matrix $\mathbf H_8$ ]] |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | [[File:P_ID1882__Mod_T_5_3_S7_neu.png|right|frame| Walsh–Spreizfolgen $(J = 8)$ und Hadamard–Matrix $\mathbf H_8$ ]] | ||
| − | |||
| − | |||
*$J - 1$ deshalb, da die ungespreizte Folge $w_0(t)$ meist nicht verwendet wird. | *$J - 1$ deshalb, da die ungespreizte Folge $w_0(t)$ meist nicht verwendet wird. | ||
*Beachten Sie bitte in der Grafik die farbliche Zuordnung zwischen den Zeilen der Hadamard–Matrix und den Spreizfolgen $w_j(t)$. | *Beachten Sie bitte in der Grafik die farbliche Zuordnung zwischen den Zeilen der Hadamard–Matrix und den Spreizfolgen $w_j(t)$. | ||
| − | *Die Matrix $\mathbf H_4$ ist gelb hinterlegt. | + | *Die Matrix $\mathbf H_4$ ist gelb hinterlegt.}} |
<br clear=all> | <br clear=all> | ||
| − | |||
| − | |||
| − | |||
| − | |||
==Zur Handhabung des Applets== | ==Zur Handhabung des Applets== | ||
| Line 70: | Line 51: | ||
[[File:Walsh Handhabung.png|right|550px]] | [[File:Walsh Handhabung.png|right|550px]] | ||
| − | '''(A)''' Auswahl | + | '''(A)''' Auswahl von $G$ ⇒ Faktor der Bandspreizung: $J= 2^G$ |
| − | '''(B)''' Auswahl der | + | '''(B)''' Auswahl der zu markierenden Walsh-Funktion $w_j$ |
<br clear=all> | <br clear=all> | ||
==Über die Autoren== | ==Über die Autoren== | ||
Dieses interaktive Berechnungstool wurde am [http://www.lnt.ei.tum.de/startseite Lehrstuhl für Nachrichtentechnik] der [https://www.tum.de/ Technischen Universität München] konzipiert und realisiert. | Dieses interaktive Berechnungstool wurde am [http://www.lnt.ei.tum.de/startseite Lehrstuhl für Nachrichtentechnik] der [https://www.tum.de/ Technischen Universität München] konzipiert und realisiert. | ||
| − | *Die erste Version wurde 2007 von [[ | + | *Die erste Version wurde 2007 von [[Biographies_and_Bibliographies/An_LNTwww_beteiligte_Studierende#Thomas_Gro.C3.9Fer_.28Diplomarbeit_LB_2006.2C_danach_freie_Mitarbeit_bis_2010.29|Thomas Großer]] im Rahmen seiner Diplomarbeit mit "FlashMX–Actionscript" erstellt (Betreuer: [[Biographies_and_Bibliographies/An_LNTwww_beteiligte_Mitarbeiter_und_Dozenten#Prof._Dr.-Ing._habil._G.C3.BCnter_S.C3.B6der_.28am_LNT_seit_1974.29|Günter Söder]]). |
| − | *2018/2019 wurde das Programm von | + | *2018/2019 wurde das Programm von [[Biographies_and_Bibliographies/An_LNTwww_beteiligte_Studierende#Carolin_Mirschina_.28Ingenieurspraxis_Math_2019.2C_danach_Werkstudentin.29|Carolin Mirschina]] (Ingenieurspraxis, Betreuer: [[Biographies_and_Bibliographies/Beteiligte_der_Professur_Leitungsgebundene_%C3%9Cbertragungstechnik#Tasn.C3.A1d_Kernetzky.2C_M.Sc._.28bei_L.C3.9CT_seit_2014.29|Tasnád Kernetzky]] ) auf "HTML5" umgesetzt und neu gestaltet. |
==Nochmalige Aufrufmöglichkeit des Applets in neuem Fenster== | ==Nochmalige Aufrufmöglichkeit des Applets in neuem Fenster== | ||
<br> | <br> | ||
| − | {{LntAppletLink| | + | {{LntAppletLink|walsh}} |
Latest revision as of 15:49, 28 May 2021
Contents
Programmbeschreibung
Dieses Applet ermöglicht die Darstellung der Hadamard-Matrizen $\mathbf{H}_J$ zur Konstruktion der Walsh-Funktionen $w_j$. Dabei können der Faktor $J$ der Bandspreizung sowie die Markierung der einzelnen Walsh-Funktionen (durch blaue Umrandung der Zeilen der Matrix) verändert werden.
Theoretischer Hintergrund
Anwendung
Die Walsh-Funktionen sind eine Gruppe von periodischen orthogonalen Funktionen. Ihr Anwendungsbereich in der digitalen Signalverarbeitung liegt vor allem in der Verwendung zur Bandspreizung bei CDMA-Systemen, beispielsweise dem Mobilfunkstandard UMTS.
- Aufgrund ihrer Orthogonalitätseigenschaften und der günstigen PKKF-Bedingungen (periodische KKF) stellen die Walsh-Funktionen für einen verzerrungsfreien Kanal und ein synchrones CDMA-System optimale Spreizfolgen dar. Nimmt man zwei beliebige Zeilen und bildet die Korrelation (Mittelung über die Produkte), so ergibt sich stets der PKKF–Wert Null.
- Bei asynchronem Betrieb (Beispiel: Uplink eines Mobilfunksystems) oder De–Orthogonalisierung aufgrund von Mehrwegeausbreitung sind dagegen Walsh–Funktionen allein zur Bandspreizung nicht unbedingt geeignet – siehe Aufgabe 5.4.
- Hinsichtlich PAKF (periodische AKF) sind diese Folgen weniger gut: Jede einzelne Walsh–Funktion hat eine andere PAKF und jede einzelne PAKF ist ungünstiger als bei einer vergleichbaren PN–Sequenz. Das bedeutet: Die Synchronisierung ist bei Walsh–Funktionen schwieriger als mit PN–Sequenzen.
Konstruktion
Die Konstruktion der Walsh-Funktionen kann rekursiv mithilfe der Hadamard-Matrizen erfolgen. Eine Hadamard-Matrix $\mathbf{H}_J$ der Ordnung $J$ ist eine $J\times J$-Matrix, die zeilenweise die $\pm 1$-Gewichte der Walsh-Folgen enthält. Die Ordnungen der Hadamard-Matrizen sind dabei auf Zweierpotenzen festgelegt, d.h. es gilt $J = 2^G$ für eine natürliche Zahl $G$. Ausgehend von $\mathbf{H}_1 = [+1]$ und
- $$ \mathbf{H}_2 = \left[ \begin{array}{rr} +1 & +1\\ +1 & -1 \\ \end{array}\right] $$
gilt der folgende Zusammenhang zur Generierung weiterer Hadamard-Matrizen:
- $$ \mathbf{H}_{2N} = \left[ \begin{array}{rr} +\mathbf{H}_N & +\mathbf{H}_N\\ +\mathbf{H}_N & -\mathbf{H}_N \\ \end{array}\right] $$
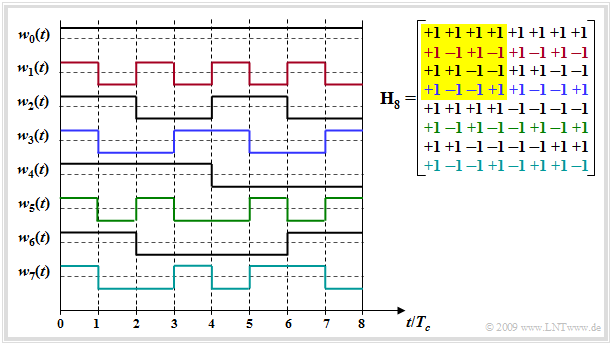
$\text{Beispiel:}$ Die Grafik zeigt die Hadamard–Matrix $\mathbf H_8$ (rechts) und die damit $J -1$ konstruierbaren Spreizfolgen.
- $J - 1$ deshalb, da die ungespreizte Folge $w_0(t)$ meist nicht verwendet wird.
- Beachten Sie bitte in der Grafik die farbliche Zuordnung zwischen den Zeilen der Hadamard–Matrix und den Spreizfolgen $w_j(t)$.
- Die Matrix $\mathbf H_4$ ist gelb hinterlegt.
Zur Handhabung des Applets
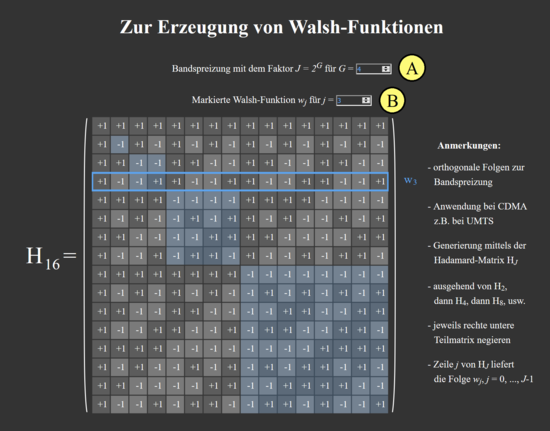
(A) Auswahl von $G$ ⇒ Faktor der Bandspreizung: $J= 2^G$
(B) Auswahl der zu markierenden Walsh-Funktion $w_j$
Über die Autoren
Dieses interaktive Berechnungstool wurde am Lehrstuhl für Nachrichtentechnik der Technischen Universität München konzipiert und realisiert.
- Die erste Version wurde 2007 von Thomas Großer im Rahmen seiner Diplomarbeit mit "FlashMX–Actionscript" erstellt (Betreuer: Günter Söder).
- 2018/2019 wurde das Programm von Carolin Mirschina (Ingenieurspraxis, Betreuer: Tasnád Kernetzky ) auf "HTML5" umgesetzt und neu gestaltet.