Difference between revisions of "Aufgaben:Exercise 1.3: Measured Step Response"
m (Text replacement - "[[Lineare_zeitinvariante_Systeme/" to "[[Linear_and_Time_Invariant_Systems/") |
|||
| (25 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Linear_and_Time_Invariant_Systems/System_Description_in_Time_Domain}} |
| − | [[File:P_ID817__LZI_A_1_3.png |right|frame| | + | [[File:P_ID817__LZI_A_1_3.png |right|frame|Measured step response]] |
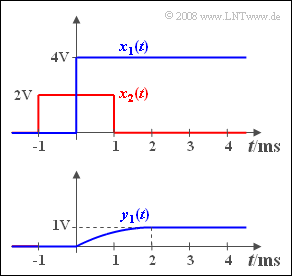
| − | + | A step-shaped signal $$x_1(t) = 4\hspace{0.05cm} {\rm V} \cdot \gamma(t)$$ (blue curve in the upper sketch) is applied to the input of a linear time-invariant (LTI) transmission system | |
| − | * | + | *with the frequency response $H(f)$ |
| − | * | + | *and the impulse response $h(t)$. |
| − | + | ||
| − | + | The measured output signal $y_1(t)$ then has the curve shown below. | |
| − | + | *With $T = 2 \,{\rm ms}$ this signal can be described in the range from $0$ to $T$ as follows: | |
| − | |||
| − | * | ||
:$$y_1(t) = 2 \hspace{0.05cm}{\rm V} \cdot\big[ {t}/{T} - 0.5 \cdot ({t}/{T})^2\big].$$ | :$$y_1(t) = 2 \hspace{0.05cm}{\rm V} \cdot\big[ {t}/{T} - 0.5 \cdot ({t}/{T})^2\big].$$ | ||
| − | * | + | *From $t = T $ on $y_1(t)$ is constantly equal $1 \,{\rm V}$. |
| − | In | + | In the last subtask '''(5)''' the output signal $y_2(t)$ is to be determined if a symmetrical rectangular pulse $x_2(t)$ of duration $T = 2 \hspace{0.15cm} {\rm ms}$ is applied to the input (see red curve in the upper graph). |
| Line 27: | Line 25: | ||
| − | '' | + | ''Please note:'' |
| − | * | + | *The exercise belongs to the chapter [[Linear_and_Time_Invariant_Systems/System_Description_in_Time_Domain|System Description in Time Domain]]. |
| − | * | + | *The rectangular pulse $x_2(t)$ can also be written as follows with $A = 2 \hspace{0.05cm} \text{V}$ : |
:$$x_2(t) = A \cdot \big [\gamma(t + {T}/{2}) - \gamma(t - {T}/{2})\big ].$$ | :$$x_2(t) = A \cdot \big [\gamma(t + {T}/{2}) - \gamma(t - {T}/{2})\big ].$$ | ||
| − | * | + | *The frequency response $H(f)$ of the LTI system considered here can be taken from the exercise description of [[Aufgaben:Exercise_3.8:_Triple_Convolution%3F|Exercise 3.8]] in the book "Signal Representation”. However, the abscissa and ordinate parameters have to be adjusted accordingly. |
| − | * | + | *For the solution of the problem on hand, though, $H(f)$ is not explicitly required. |
| Line 38: | Line 36: | ||
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {What statements can be made about the LTI system based on the graph? |
|type="[]"} | |type="[]"} | ||
| − | - $H(f)$ | + | - $H(f)$ describes an acausal system. |
| − | + $H(f)$ | + | + $H(f)$ describes a causal system. |
| − | + $H(f)$ | + | + $H(f)$ describes a low-pass filter. |
| − | - $H(f)$ | + | - $H(f)$ describes a high-pass filter. |
| − | { | + | {What is the direct signal transmission factor? |
|type="{}"} | |type="{}"} | ||
$H(f = 0) \ =\ $ { 0.25 } | $H(f = 0) \ =\ $ { 0.25 } | ||
| − | { | + | {What is the step response $σ(t)$? What is its value at $t = T/2$ ? |
|type="{}"} | |type="{}"} | ||
$σ(t = \rm 1 \: ms) \ = \ $ { 0.1875 5% } | $σ(t = \rm 1 \: ms) \ = \ $ { 0.1875 5% } | ||
| − | { | + | {Compute the impulse response $h(t)$ of the system. What values does it have at times $t = T/2$ and $t = T$? |
|type="{}"} | |type="{}"} | ||
$h(t = \rm 1 \: ms) \ =\ $ { 125 } $\text {1/s}$ | $h(t = \rm 1 \: ms) \ =\ $ { 125 } $\text {1/s}$ | ||
$h(t = \rm 2 \: ms) \ =\ ${ 0. } $\text {1/s}$ | $h(t = \rm 2 \: ms) \ =\ ${ 0. } $\text {1/s}$ | ||
| − | { | + | {The rectangular pulse $x_2(t)$ is applied to the input. What is the output signal $y_2(t)$ at the times $t_1 = -1 \text { ms}$, $t_2 = 0$, $t_3 = +1 \text { ms}$ and $t_4 = +2 \text { ms}$? |
|type="{}"} | |type="{}"} | ||
$y_2(t = t_1) \ =\ $ { 0. } $\text {V}$ | $y_2(t = t_1) \ =\ $ { 0. } $\text {V}$ | ||
| Line 74: | Line 72: | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' <u>Approaches 2 und 3</u> are correct: |
| − | * | + | *The output signal is $y_1(t)=0$ as long as the input signal is $x_1(t) = 0$. This means that there is a causal system on hand. |
| − | * | + | *One could have arrived at the same result just by considering the statement "the output signal was measured". Only causal systems are realisable and only in realisable systems something can be measured. |
| − | * | + | *The input signal $x_1(t)$ can be interpreted as a direct (DC) signal for very large times $(t \gg 0)$. If $H(f)$ was a high-pass filter, then $y_1(t)$ would have to go towards zero for $t → ∞$. This means: $H(f)$ represents a low-pass filter. |
| − | '''(2)''' | + | '''(2)''' The direct signal transmission factor can be read from $x_1(t)$ and $y_1(t)$ when the transient has decayed: |
:$$H(f =0) = \frac{y_1(t \rightarrow \infty)}{x_1(t \rightarrow \infty)}= | :$$H(f =0) = \frac{y_1(t \rightarrow \infty)}{x_1(t \rightarrow \infty)}= | ||
\frac{ {\rm 1\, V} }{ {\rm 4\, V} } \hspace{0.15cm}\underline{= 0.25}.$$ | \frac{ {\rm 1\, V} }{ {\rm 4\, V} } \hspace{0.15cm}\underline{= 0.25}.$$ | ||
| − | '''(3)''' | + | '''(3)''' The step response $σ(t)$ is equal to the output signal $y(t)$, if $x(t) = γ(t)$ is applied to the input. |
| − | * | + | *Because of $x_1(t) = 4 \hspace{0.05cm} \rm {V} · γ(t)$ the following holds in the range from $0$ to $T = 2 \ \rm ms$: |
:$$\sigma(t) = \frac{y_1(t)}{ {\rm 4\, V} } = 0.5 \cdot\big( {t}/{T} - 0.5 ({t}/{T})^2\big).$$ | :$$\sigma(t) = \frac{y_1(t)}{ {\rm 4\, V} } = 0.5 \cdot\big( {t}/{T} - 0.5 ({t}/{T})^2\big).$$ | ||
| − | * | + | *At time $t = T = 2 \ \rm ms$ the step response reaches its final value $0.25$. |
| − | * | + | *For $t = T/2 = 1 \hspace{0.15cm} \rm ms$ the numerical value $3/16 \; \underline{\: = \: 0.1875}$ is obtained. |
| − | * | + | *Please note that the step response $σ(t)$ as well as the step function $γ(t)$ have no unit. |
| − | [[File:P_ID840__LZI_A_1_3d.png | + | [[File:P_ID840__LZI_A_1_3d.png|rechts|frame |Impulse response]] |
| − | '''(4)''' | + | '''(4)''' The step response $σ(t)$ is the integral over the impulse response $h(t)$. |
| − | * | + | *Thus, $h(t)$ is obtained from $σ(t)$ by differentiation with respect to time. |
| − | * | + | *Therefore, in the range $0 < t < T$ the following is valid: |
:$$h(t) = \frac{{\rm d}\hspace{0.1cm}\sigma(t)}{{\rm d}t}= 0.5 \cdot\left( \frac{1}{T} - 0.5 (\frac{2t}{T^2})\right) = \frac{0.5}{T} \cdot (1- \frac{t}{T})$$ | :$$h(t) = \frac{{\rm d}\hspace{0.1cm}\sigma(t)}{{\rm d}t}= 0.5 \cdot\left( \frac{1}{T} - 0.5 (\frac{2t}{T^2})\right) = \frac{0.5}{T} \cdot (1- \frac{t}{T})$$ | ||
:$$\Rightarrow \hspace{0.2cm} h(t = {\rm 1\, ms}) = h(t = T/2) = \frac{0.25}{T} \hspace{0.15cm}\underline{= 125 \cdot{1}/{ {\rm s} } },$$ | :$$\Rightarrow \hspace{0.2cm} h(t = {\rm 1\, ms}) = h(t = T/2) = \frac{0.25}{T} \hspace{0.15cm}\underline{= 125 \cdot{1}/{ {\rm s} } },$$ | ||
:$$\Rightarrow \hspace{0.2cm} h(t = {\rm 2\, ms}) = h(t = T) \hspace{0.15cm}\underline{= 0}.$$ | :$$\Rightarrow \hspace{0.2cm} h(t = {\rm 2\, ms}) = h(t = T) \hspace{0.15cm}\underline{= 0}.$$ | ||
| − | * | + | *For $t < 0$ and $t ≥ T$, $h(t)=0$ always holds. |
| − | * | + | *The value $h(t = 0)$ at exactly $t = 0$ must be determined from the mean value between the left-hand and right-hand limits: |
:$$h(t=0) = {1}/{2} \cdot \left[ \lim_{\varepsilon | :$$h(t=0) = {1}/{2} \cdot \left[ \lim_{\varepsilon | ||
\hspace{0.03cm} \to \hspace{0.03cm}0} h(- \varepsilon)+ \lim_{\varepsilon | \hspace{0.03cm} \to \hspace{0.03cm}0} h(- \varepsilon)+ \lim_{\varepsilon | ||
| Line 112: | Line 110: | ||
| − | [[File:P_ID829__LZI_A_1_3e.png | + | [[File:P_ID829__LZI_A_1_3e.png | rechts|frame| Rectangular response]] |
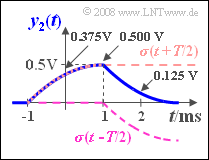
| − | '''(5)''' | + | '''(5)''' The symmetrical rectangular pulse $x_2(t)$ can also be represented as the difference of two steps shifted by $±T/2$: |
:$$x_2(t) = A \cdot \big[\gamma(t + {T}/{2}) - \gamma(t - {T}/{2})\big].$$ | :$$x_2(t) = A \cdot \big[\gamma(t + {T}/{2}) - \gamma(t - {T}/{2})\big].$$ | ||
| − | * | + | *Hence, the output signal is equal to the difference of two step responses shifted by $±T/2$: |
:$$y_2(t) = A \cdot \big[\sigma(t + {T}/{2}) - \sigma(t - {T}/{2})\big].$$ | :$$y_2(t) = A \cdot \big[\sigma(t + {T}/{2}) - \sigma(t - {T}/{2})\big].$$ | ||
| − | * | + | *For $t = \: -T/2 = -1\ \rm ms$ the following holds: $y_2(t) \;\underline{ = 0}$. |
| − | * | + | *For the other time points considered the following is obtained as indicated in the graph: |
:$$y_2(t = 0) = A \cdot \big[\sigma(0.5 \cdot T) - \sigma(-0.5 \cdot T)\big] = | :$$y_2(t = 0) = A \cdot \big[\sigma(0.5 \cdot T) - \sigma(-0.5 \cdot T)\big] = | ||
{\rm 2\, V}\cdot \left[0.1875 - 0\right] \hspace{0.15cm}\underline{= {\rm 0.375\, V}},$$ | {\rm 2\, V}\cdot \left[0.1875 - 0\right] \hspace{0.15cm}\underline{= {\rm 0.375\, V}},$$ | ||
| Line 131: | Line 129: | ||
| − | [[Category: | + | [[Category:Linear and Time-Invariant Systems: Exercises|^1.2 System Description in Time Domain^]] |
Latest revision as of 11:21, 12 July 2021
A step-shaped signal $$x_1(t) = 4\hspace{0.05cm} {\rm V} \cdot \gamma(t)$$ (blue curve in the upper sketch) is applied to the input of a linear time-invariant (LTI) transmission system
- with the frequency response $H(f)$
- and the impulse response $h(t)$.
The measured output signal $y_1(t)$ then has the curve shown below.
- With $T = 2 \,{\rm ms}$ this signal can be described in the range from $0$ to $T$ as follows:
- $$y_1(t) = 2 \hspace{0.05cm}{\rm V} \cdot\big[ {t}/{T} - 0.5 \cdot ({t}/{T})^2\big].$$
- From $t = T $ on $y_1(t)$ is constantly equal $1 \,{\rm V}$.
In the last subtask (5) the output signal $y_2(t)$ is to be determined if a symmetrical rectangular pulse $x_2(t)$ of duration $T = 2 \hspace{0.15cm} {\rm ms}$ is applied to the input (see red curve in the upper graph).
Please note:
- The exercise belongs to the chapter System Description in Time Domain.
- The rectangular pulse $x_2(t)$ can also be written as follows with $A = 2 \hspace{0.05cm} \text{V}$ :
- $$x_2(t) = A \cdot \big [\gamma(t + {T}/{2}) - \gamma(t - {T}/{2})\big ].$$
- The frequency response $H(f)$ of the LTI system considered here can be taken from the exercise description of Exercise 3.8 in the book "Signal Representation”. However, the abscissa and ordinate parameters have to be adjusted accordingly.
- For the solution of the problem on hand, though, $H(f)$ is not explicitly required.
Questions
Solution
- The output signal is $y_1(t)=0$ as long as the input signal is $x_1(t) = 0$. This means that there is a causal system on hand.
- One could have arrived at the same result just by considering the statement "the output signal was measured". Only causal systems are realisable and only in realisable systems something can be measured.
- The input signal $x_1(t)$ can be interpreted as a direct (DC) signal for very large times $(t \gg 0)$. If $H(f)$ was a high-pass filter, then $y_1(t)$ would have to go towards zero for $t → ∞$. This means: $H(f)$ represents a low-pass filter.
(2) The direct signal transmission factor can be read from $x_1(t)$ and $y_1(t)$ when the transient has decayed:
- $$H(f =0) = \frac{y_1(t \rightarrow \infty)}{x_1(t \rightarrow \infty)}= \frac{ {\rm 1\, V} }{ {\rm 4\, V} } \hspace{0.15cm}\underline{= 0.25}.$$
(3) The step response $σ(t)$ is equal to the output signal $y(t)$, if $x(t) = γ(t)$ is applied to the input.
- Because of $x_1(t) = 4 \hspace{0.05cm} \rm {V} · γ(t)$ the following holds in the range from $0$ to $T = 2 \ \rm ms$:
- $$\sigma(t) = \frac{y_1(t)}{ {\rm 4\, V} } = 0.5 \cdot\big( {t}/{T} - 0.5 ({t}/{T})^2\big).$$
- At time $t = T = 2 \ \rm ms$ the step response reaches its final value $0.25$.
- For $t = T/2 = 1 \hspace{0.15cm} \rm ms$ the numerical value $3/16 \; \underline{\: = \: 0.1875}$ is obtained.
- Please note that the step response $σ(t)$ as well as the step function $γ(t)$ have no unit.
(4) The step response $σ(t)$ is the integral over the impulse response $h(t)$.
- Thus, $h(t)$ is obtained from $σ(t)$ by differentiation with respect to time.
- Therefore, in the range $0 < t < T$ the following is valid:
- $$h(t) = \frac{{\rm d}\hspace{0.1cm}\sigma(t)}{{\rm d}t}= 0.5 \cdot\left( \frac{1}{T} - 0.5 (\frac{2t}{T^2})\right) = \frac{0.5}{T} \cdot (1- \frac{t}{T})$$
- $$\Rightarrow \hspace{0.2cm} h(t = {\rm 1\, ms}) = h(t = T/2) = \frac{0.25}{T} \hspace{0.15cm}\underline{= 125 \cdot{1}/{ {\rm s} } },$$
- $$\Rightarrow \hspace{0.2cm} h(t = {\rm 2\, ms}) = h(t = T) \hspace{0.15cm}\underline{= 0}.$$
- For $t < 0$ and $t ≥ T$, $h(t)=0$ always holds.
- The value $h(t = 0)$ at exactly $t = 0$ must be determined from the mean value between the left-hand and right-hand limits:
- $$h(t=0) = {1}/{2} \cdot \left[ \lim_{\varepsilon \hspace{0.03cm} \to \hspace{0.03cm}0} h(- \varepsilon)+ \lim_{\varepsilon \hspace{0.03cm} \to \hspace{0.03cm} 0} h(+ \varepsilon)\right] = \left[ 0 + {0.5}/{T}\right] = {0.25}/{T}= 250 \cdot{1}/{ {\rm s} }.$$
(5) The symmetrical rectangular pulse $x_2(t)$ can also be represented as the difference of two steps shifted by $±T/2$:
- $$x_2(t) = A \cdot \big[\gamma(t + {T}/{2}) - \gamma(t - {T}/{2})\big].$$
- Hence, the output signal is equal to the difference of two step responses shifted by $±T/2$:
- $$y_2(t) = A \cdot \big[\sigma(t + {T}/{2}) - \sigma(t - {T}/{2})\big].$$
- For $t = \: -T/2 = -1\ \rm ms$ the following holds: $y_2(t) \;\underline{ = 0}$.
- For the other time points considered the following is obtained as indicated in the graph:
- $$y_2(t = 0) = A \cdot \big[\sigma(0.5 \cdot T) - \sigma(-0.5 \cdot T)\big] = {\rm 2\, V}\cdot \left[0.1875 - 0\right] \hspace{0.15cm}\underline{= {\rm 0.375\, V}},$$
- $$y_2(t = T/2) = y_2(t = 1\,{\rm ms}) =A \cdot \big[\sigma( T) - \sigma(0)\big] = {\rm 2\, V}\cdot \left[0.25 - 0\right] \hspace{0.15cm}\underline{= {\rm 0.5\, V}},$$
- $$y_2(t = T) = A \cdot \big[\sigma(1.5 \cdot T) - \sigma(0.5 \cdot T)\big] = {\rm 2\, V}\cdot \big[0.25 - 0.1875\big] \hspace{0.15cm}\underline{= {\rm 0.125\, V}}.$$