Difference between revisions of "Aufgaben:Exercise 2.3Z: About the LZ77 Coding"
| Line 38: | Line 38: | ||
*The original literature [LZ77] on this method is: <br> Ziv, J.; Lempel, A.: A Universal Algorithm for Sequential Data Compression. In: IEEE Transactions on Information Theory, no. 3, vol. 23, 1977, p. 337–343. | *The original literature [LZ77] on this method is: <br> Ziv, J.; Lempel, A.: A Universal Algorithm for Sequential Data Compression. In: IEEE Transactions on Information Theory, no. 3, vol. 23, 1977, p. 337–343. | ||
| − | * [[Aufgaben: | + | * [[Aufgaben:Exercise_2.4:_About_the_LZW_algorithm|Exercise 2.3]] and [[Aufgaben:Exercise_2.4:_About_the_LZW_algorithm|Exercise 2.4]] deal with other Lempel–Ziv methods in a similar way. |
Revision as of 16:01, 12 July 2021
In Exercise 2.3, you were supposed to compress "BARBARA–BAR" (string of length $11$, four different characters) using the LZ78 algorithm.
In this exercise we use the same text to demonstrate LZ77 compression. To note:
- While the successor "LZ78" successively builds a global dictionary, "LZ77" uses a local dictionary.
- The LZ77 method works with a "Sliding Window" that is gradually shifted over the input text.
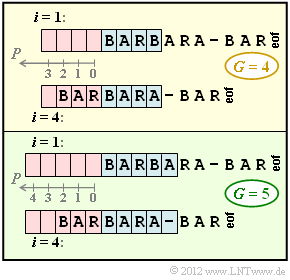
- This "sliding window" is divided into the "preview buffer" (highlighted in blue in the graphic) and the "search buffer" (highlighted in red). Both buffers have a size of $G$ memory locations each.
- Each coding step $i$ is characterised by a triple $(P,\ L,\ Z)$. Here, $P$ and $L$ are integers and $Z$ is a character. Transmitted are the binary representations of $P$, $L$ and $Z$.
- After transmission, the sliding window is shifted one or more positions to the right and the next coding step $i + 1$ begins.
The upper diagram shows the initial allocation with the buffer size $G = 4$ at the times $i = 1$ as well as $i = 4$.
- At time $i = 1$ , the search buffer is empty, so the coder output is $(0, 0,$ B$)$ .
- After the shift by one position, the search buffer contains a B, but no string that begins with A. The second number triple is therefore $(0, 0,$ A$)$.
- The output for $i = 3$ is $(0, 0,$ R$)$, since there is no string beginning with R in the search buffer even now.
The snapshot at time $i = 4$ is also shown in the graphic. The search is now for the character string in the search buffer that best matches the preview text BARA . A number triple $(P,\ L,\ Z)$, is transmitted again, but now with the following meaning:
- $P$ indicates the position in the (red) search buffer where the match starts. The $P$ values of the individual memory locations can be seen in the graphic.
- $L$ denotes the number of characters in the search buffer that, starting at $P$, match the current string in the preview buffer.
- Finally $Z$ denotes the first character in the preview buffer that differs from the matching string found in the search buffer.
The larger the LZ77 parameter $G$ , the easier it is to find the longest possible match. In subtask (4) you will notice that the LZ77 encoding with $G = 5$ gives a better result than the one with $G = 4$.
- However, because of the later binary representation of $P$, one will always choose $G$ as a power of two, so that $G$ can be represented with $\log_2 \ P$ bits $(G = 8$ ⇒ three-digit binary number $P)$.
- This means that a "Sliding Window" with $G = 5$ has rather little practical relevance.
Hints:
- The task belongs to the chapter Compression according to Lempel, Ziv and Welch.
- In particular, reference is made to the page LZ77 – the basic form of the Lempel-Ziv algorithms .
- The original literature [LZ77] on this method is:
Ziv, J.; Lempel, A.: A Universal Algorithm for Sequential Data Compression. In: IEEE Transactions on Information Theory, no. 3, vol. 23, 1977, p. 337–343.
- Exercise 2.3 and Exercise 2.4 deal with other Lempel–Ziv methods in a similar way.
Questions
Solution
(1) Richtig ist der Lösungsvorschlag 3.
- Im Vorschaupuffer steht zum betrachteten Zeitpunkt $i = 4$ die Zeichenfolge BARA.
- Im Suchpuffer steht in den letzten drei Stellen BAR:
- $$P = 2\hspace{0.05cm},\hspace{0.2cm}L = 3\hspace{0.05cm},\hspace{0.2cm}Z = \boldsymbol{\rm A}\hspace{0.05cm}.$$
(2) Richtig sind die beiden ersten Lösungsvorschläge:
- Der Bindestrich findet sich zum Zeitpunkt $i = 5$ nicht im Suchpuffer.
- Ausgegeben wird $(0, 0,$ –$)$.
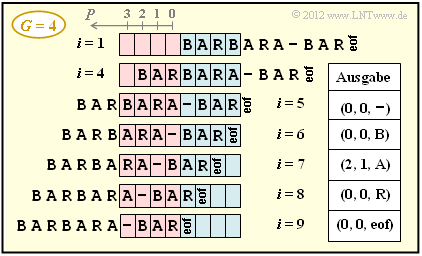
(3) Die obere Grafik zeigt das Sliding–Window und die Coderausgabe zu den Zeiten $i>5$.
- Nach $i = 9$ Codierschritten ist der Codiervorgang unter Berücksichtigung von eof beendet ⇒ $\underline{i_{\rm Ende} = 9}$.
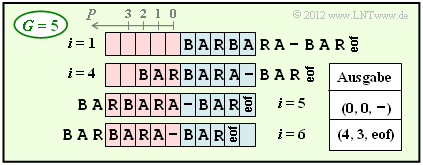
(4) Bei größerer Puffergröße $(G = 5$ anstelle von $G = 4)$ ist die Codierung schon nach dem 6. Codierschritt abgeschlossen ⇒ $\underline{i_{\rm Ende} = 6}$.
- Ein Vergleich der beiden Grafiken zeigt, dass sich für $G = 5$ gegenüber $G = 4$ bis einschließlich $i = 5$ nichts ändert.
- Aufgrund des größeren Puffers lässt sich aber nun BAR gemeinsam mit eof (end-of-file) in einem einzigen Schritt codieren, während mit $G = 4$ hierfür vier Schritte notwendig waren.
(5) Richtig ist nur die Aussage 1.
- Ein Nachteil von LZ77 ist das lokale Wörterbuch. Eigentlich schon bekannte Phrasen können nicht für die Datenkomprimierung verwendet werden, wenn sie mehr als $G$ Zeichen vorher im Text aufgetreten sind. Dagegen sind bei LZ78 alle Phrasen im globalen Wörterbuch abgelegt.
- Richtig ist zwar, dass bei LZ78 nur Pärchen $(I, \ Z)$ übertragen werden müssen, während bei LZ77 jeder Codierschritt durch ein Triple $(P, \ L, \ Z)$ gekennzeichnet ist. Das bedeutet aber noch nicht, dass pro Codierschritt auch weniger Bit übertragen werden müssen.
- Betrachten wir beispielhaft die Puffergröße $G = 8$. Bei LZ77 muss man dann $P$ mit drei Bit und $L$ mit vier Bit dargestellen. Beachten Sie bitte, dass die gefundene Übereinstimmung zwischen Vorschaupuffer und Suchpuffer auch im Vorschaupuffer enden darf.
- Das neue Zeichen $Z$ benötigt bei LZ78 genau die gleiche Bitanzahl wie bei LZ77 (nämlich zwei Bit), wenn man wie hier vom Symbolumfang $M = 4$ ausgeht.
- Die Aussage 2 wäre nur dann richtig, wenn $N_{\rm I}$ kleiner wäre als $N_{\rm P}+ N_{\rm L}$, beispielsweise $N_{\rm I} = 6$. Das würde aber bedeuten, dass man die Wörterbuchgröße auf $I = 2^6 = 64$ begrenzen müsste. Dies reicht für große Dateien nicht aus.
- Unsere Überschlagsrechnung basiert allerdings auf einer einheitlichen Bitanzahl für den Index $I$. Mit variabler Bitanzahl für den Index kann man etliche Bit einsparen, indem man $I$ nur mit so vielen Bit überträgt, wie es für den Codierschritt $i$ erforderlich ist.
- Prinzipiell ändert das aber nichts an der Beschränkung der Wörterbuchgröße, was bei großen Dateien stets zu Problemen führen wird.