Aufgaben:Exercise 2.4Z: LZW Coding and Decoding again

• Return to book

Snapshots of the LZW dictionaries

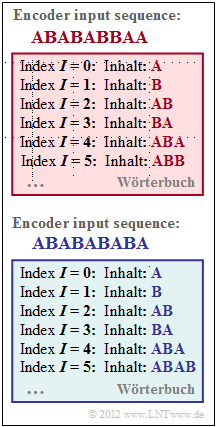
The graph shows snapshots of the dictionary created during LZW coding of the input symbol sequence.

• The upper graph is for input symbol sequence  ABABABBAA.
• The lower dictionary is created during LZW coding of the sequence  ABABABABA.

In both cases, it is assumed that no characters other than  A  and  B  can occur at later times.

In LZW decoding, the same dictionaries are created, but then the dictionary entries occur one step later.  In subtask  (3)  the question is asked for which coding step or for which decoding step the two snapshots shown are valid.

In LZW coding, an index $I$ is selected for each coding step $i$ and transmitted (binary).  The character pair AB is represented by the index $I = 2$ in the two dictionaries.  Here we consider the index $I$ as a decimal number and leave the binary representation out of consideration for this task.

With LZW decoding, a character or character sequence is generated in the same way from each index  $I$  with the help of the dictionary, for example  $I = 1$  leads to the character  B  and  $I = 2$  to the character pair  AB.

If a dictionary entry with the desired index  $I$  is actually found, the decoding runs smoothly. However, this is not always the case:

• If a new index  $I$  is entered during encoding at step  $i$  and this  $I$  is at the same time the encoding result of the step, this index is not yet occupied in the dictionary at decoding step  $i$ .  The reason for this is that with the decoder the entries are made one step later than with the coder.
• In the case of a binary input sequence  $($all characters are  A  or  B$)$  , a special rule must always be applied in LZW decoding if the entry with index  $I = i$  was made in coding step  $i$ .

This special rule shall be illustrated by an example:

• For step  $i$  there is no entry in the decoder dictionary matching index  $I$ .
• We assume that in the previous step  $(i- 1)$  the decoding result was  ABBABA .
• Then we add the first character of the sequence to this string.   Here:  ABBABAA.
• Then one enters the sequence  ABBABAA  into the dictionary under index  $I$ .

Hints:

• The exercise belongs to the chapter  Compression according to Lempel, Ziv and Welch.
• In particular, reference is made to the pages 

LZ77 - the basic form of Lempel-Ziv algorithms,

Lempel-Ziv coding with variable index bit length,

Decoding of the LZW algorithm.

• Also, when solving this task, note that the LZW algorithm does not assume an empty dictionary.
• Rather, the indices  $I = 0$  to  $I = M- 1$  contain all  $M$  permissible characters of the alphabet.

Questions

1

Code the input sequence  ABABABBAA  according to the above diagram.  Which indices  $I_i$  result for the steps  $i=1$, ... , $i=5$?

$I_1 \ = \ $

$I_2 \ = \ $

$I_3 \ = \ $

$I_4 \ = \ $

$I_5 \ = \ $

2

Now code the input sequence  ABABABABA  according to the diagram below.  Specify the indices  $I_i$  for the steps  $i=4$  and  $i=5$ .

$I_4 \ = \ $

$I_5 \ = \ $

3

For which step  $i$  does the snapshot of the dictionary shown on the input page apply with respect to

$\text{Encoding:} \ \ i \ = \ $

$\text{Decoding:} \ \ i \ = \ $

4

When does one have to resort to the decoding special case rule?

	When decoding  ABABABBAA  in step  $i = 4$.
	When decoding  ABABABABA  in step  $i = 4$.
	When decoding  ABABABABA  in step  $i = 5$.

Solution

Solution

(1)  We use  $W(I)$  to denote a field (array), that describes the dictionary and whose elements contain characters or strings.  

• The encoding of  ABABABBAA  then proceeds as follows:

$i = 1$:     A    →   $\underline{I=0}$,   $W(I = 2) =$ AB,

$i = 2$:     B    →   $\underline{I=1}$,   $W(I = 3) =$ BA,

$i = 3$:     AB →   $\underline{I=2}$,   $W(I = 4) =$ ABA,

$i = 4$:     AB →   $\underline{I=2}$,   $W(I = 5) =$ ABB,

$i = 5$:     BA →   $\underline{I=3}$,   $W(I = 6) =$ BAA.

• Note that the last character  $($A$)$  of the input string  ABABABBAA  at time  $i = 5$  is already considered in the dictionary entry but has not yet been encoded.

(2)  For the steps  $i = 1$  to  $i = 3$  nothing changes compared to subtask  (1).

• Afterwards, the following applies:

$i = 4$:     ABA →   $\underline{I=4}$,   $W(I = 5) =$ ABAB,

$i = 5$:     BA →   $\underline{I=3}$,   coding completed, no new dictionary entry possible.

(3)  The comparison with above results shows:

• The dictionary of the coder has the entries shown exactly after  $\underline{i=4}$  coding steps.
• With the decoder, on the other hand, there is a time delay of one step:   $\underline{i=5}$.

(4)  Solution suggestion 2 is correct:

• The special case regulation of the decoding is necessary  (in the present example)  if the index  $I =i$  is output in the coding step  $i$ .
• During decoding, it then does not find the required assignment  "Index  →  String"  since the generated dictionary at time  $i$  only contains entries with indices  $I < i$ .
• For the sequence  ABABABBAA    $I < i$ always applies according to subtask  (1) .
• In contrast, the following indices would result for the sequence  ABABABABA :

$$i = 1\hspace{-0.15cm}: \hspace{0.15cm} I = 0\hspace{0.05cm}, \hspace{0.5cm}i = 2\hspace{-0.15cm}: \hspace{0.15cm}I = 1\hspace{0.05cm}, \hspace{0.5cm}i = 3\hspace{-0.15cm}: \hspace{0.15cm}I = 2\hspace{0.05cm}, \hspace{0.5cm}\underline{i = 4\hspace{-0.15cm}: \hspace{0.15cm}I = 4}\hspace{0.05cm}, \hspace{0.5cm}i = 5\hspace{-0.15cm}: \hspace{0.15cm}I = 3\hspace{0.05cm}. $$

Here is a summary of the entire decoding of  ABABABABA:

• The pre-assignment of the dictionary includes  $(I=0$:  A$)$     and  $(I=1$:  B$)$.

• Then with the dictionary array  $W(I)$:

$i = 1$:     decoding   $I=0$   →   A,

$i = 2$:     decoding  $I=1$   →   B,       $W(I = 2) =$ AB,

$i = 3$:     decoding  $I=2$   →   AB,     $W(I = 3) =$ BA,

$i = 4$:     An entry with index  $I = 4$  is not present   ⇒   Special case rule:
                  One takes the last decoding result  $($here  AB$)$ and adds the first character of this sequence at the end   ⇒   ABA.
                  Then  ABA  is stored in the dictionary under  index  $I = 4$ .

$i = 5$:     Decoding   $I=3$   →   BA.             End of the decoder input sequence.