Difference between revisions of "Aufgaben:Exercise 2.9: Huffman Decoding after Errors"
From LNTwww
| Line 117: | Line 117: | ||
| − | [[Category:Information Theory: Exercises|^2.3 | + | [[Category:Information Theory: Exercises|^2.3 Entropy Coding according to Huffman^]] |
Revision as of 14:00, 16 July 2021
Wir betrachten die Huffman–Codierung gemäß folgender Zuordnung:
- $\rm A$ → 1, $\rm B$ → 01, $\rm C$ → 001, $\rm D$ → 000.
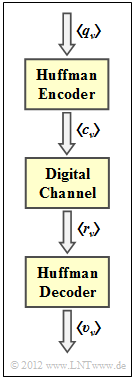
Die Codierung nach Huffman ist stets verlustlos. Das bedeutet:
- Decodiert man die Codesymbolfolge $\langle c_\nu \rangle$ nach dem Huffman–Codierer sofort wieder, so ist das Decodierergebnis $\langle v_\nu \rangle$ gleich der Quellensymbolfolge $\langle q_\nu \rangle$.
- Stimmt dagegen die Empfangsfolge $\langle r_\nu \rangle$ aufgrund von Fehlern bei der Übertragung $($0 → 1, 1 → 0$)$ mit der erzeugten Codefolge $\langle c_\nu \rangle$ nicht überein, so kann es zu einer Fehlerfortpflanzung kommen.
- Ein einziger Bitfehler kann dann dazu führen, dass (nahezu) alle nachfolgenden Zeichen falsch decodiert werden.
Hinweise:
- Die Aufgabe gehört zum Kapitel Entropiecodierung nach Huffman.
- Insbesondere wird auf die Seite Einfluss von Übertragungsfehlern auf die Decodierung Bezug genommen.
Fragebogen
Musterlösung
(1) Richtig ist der Lösungsvorschlag 3:
- Nachfolgend sehen Sie die durch Hochkommata eingeteilte Codesymbolfolge:
- $$\langle c_\nu \rangle = \rm \langle 1'01'001'000'1'1'000'01'001'1 \rangle .$$
- Diese gehört zur folgenden Quellensymbolfolge:
- $$\langle c_\nu \rangle = \rm \langle ABCDAADBCA \rangle .$$
(2) Richtig ist der Lösungsvorschlag 1:
- Mit einem Bitfehler an der Position 1 erhält man für die Empfangsfolge:
- $$\langle r_\nu \rangle = \rm \langle 00100100011000010011 \rangle .$$
- Die Hochkommata verdeutlichen die einzelnen Blöcke der Decodierung:
- $$\langle r_\nu \rangle = \rm \langle 001'001'000'1'1'000'01'001'1 \rangle .$$
- Dies führt zur folgenden Sinkensymbolfolge:
- $$\langle v_\nu \rangle = \rm \langle CCDAADBCA \rangle .$$
Interpretation:
- $\rm AB$ wird durch $\rm C$ ersetzt, der weitere Text $\rm CDAADBCA$ ist unverändert, allerdings um eine Position verschoben.
- Vergleicht man jedoch die ersten neun Symbole des Originals mit der Decodierung Stelle für Stelle, wie es ein Automat machen würde, so erkennt man acht unterschiedliche Symbole.
(3) Richtig sind die Antworten 1 und 3:
- Durch einen zusätzlichen Bitfehler an Position 2 $\rm (0 → 1)$ wird $\rm AB$ zu $\rm BA$ verfälscht, aber alle weiteren Symbole wieder richtig erkannt.
- Ein zusätzlicher Bitfehler an Position 15 $\rm (0 → 1)$ führt zu
- $$\langle r_\nu \rangle = \rm {\langle \underline{0}01'001'000'1'1'000'\underline{1}'1'001'1 \rangle} \hspace{0.3cm}\Rightarrow \hspace{0.3cm}\langle \it v_\nu \rangle = \rm \langle \underline{C}CDAAD\underline{AA}CA \rangle .$$
- Durch den Bitfehler an Position 1 $\rm (1 → 0)$ wird $\rm AB$ in $\rm C$ verfälscht, also ein Zeichen "verschluckt". Durch den zusätzlichen Bitfehler an Position 15 $\rm (0 → 1)$ wird aus $\rm B$ das Tupel $\rm AA$. Danach werden alle Symbole an der richtigen Position richtig erkannt, beginnend mit $\rm CA$.
- Ein zusätzlicher Bitfehler an Position 10 $\rm (1 → 0)$ führt dagegen zu
- $$\langle r_\nu \rangle = \rm \langle \underline{0}01'001'000'\underline{0}'1'000'0'1'001'1 \rangle \hspace{0.3cm}\Rightarrow \hspace{0.3cm}\langle \it v_\nu \rangle = \rm \langle \underline{C}CDAAD\underline{B}CA \rangle .$$
- Der Bitfehler an Position 10 macht aus $\rm AA$ ein $\rm B$. Insgesamt verschluckt so der Decoder zwei Zeichen. Alle nachfolgend decodierten Zeichen stehen dann nicht an der richtigen Position.
(4) Richtig ist der Lösungsvorschlag 2:
- Der erste Bitfehler an der Position 6 $\rm (1 → 0)$ liefert
- $$\langle r_\nu \rangle = \rm \langle 101'00\underline{0}'000'1'000'0'1'001'1 \rangle \hspace{0.3cm}\Rightarrow \hspace{0.3cm}\langle \it v_\nu \rangle = \rm \langle AB\underline{D}DAADBCA \rangle .$$
- Aus dem ersten $\rm C$ wird ein $\rm D$. Alle anderen Symbole werden richtig decodiert.