Aufgaben:Exercise 1.4Z: Everything Rectangular

• Return to book

Periodic rectangular signal and
filter with rectangular impulse response

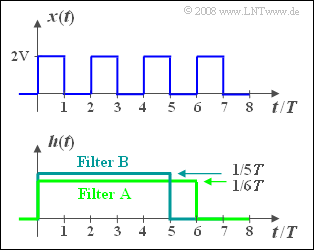
We consider the periodic rectangular signal  $x(t)$ , whose periodic duration is  $T_0 = 2T$ , according to the sketch above.

• This signal has spectral components at the fundamental frequency  $f_0 = 1/T_0 = 1/(2T)$  and at all odd multiples thereof, that is, at  $3f_0$,  $5f_0,$  and so on. In addition, there is a direct component.

• For this purpose, we consider two filters  $\rm A$  and  $\rm B$  each with rectangular impulse response  $h_{\rm A}(t)$  with duration  $6T$  and  $h_{\rm B}(t)$  with duration  $5T$, respectively.
• The heights of the two impulse responses are such that the areas of the rectangles each add up to  $1$ .

Please note:

• The exercise belongs to the chapter  System Description in Time Domain.
• For information on convolution, see the chapter  convolution theorem and operation  in the book "Signal Representation”.
• We also refer you to the interactive applet  Zur Verdeutlichung der graphischen Faltung.

Questions

1

Compute the output signal  $y_{\rm A}(t)$  of the filter  $\rm A$, in particular the values at  $t = 0$  and  $t = T$.

$y_{\rm A}(t = 0) \ =\ $  $\rm V$

$y_{\rm A}(t = T) \ =\ $  $\rm V$

2

Give the absolute value function  $|H_{\rm A}(f)|$ .   What value is obtained at frequency  $f = f_0$?
Interpret the result of the subtask  (1).

$|H_{\rm A}(f = f_0)| \ =\ $

3

Compute the output signal  $y_{\rm B}(t)$  of the filter  $\rm B$, in particular the values at  $t = 0$  and  $t = T$.

$y_{\rm B}(t = 0) \ =\ $  $\rm V$

$y_{\rm B}(t = T) \ =\ $  $\rm V$

4

What is the absolute value function  $|H_{\rm B}(f)|$, especially at frequencies  $f = f_0$  and  $f = 3 · f_0$?
Use this to interpret the result of the subtask  (3).

$|H_{\rm B}(f = f_0)| \ =\ $

$|H_{\rm B}(f = 3f_0)| \ =\ $

Solution

Solution

(1)  Das Ausgangssignal ist das Ergebnis der Faltungsoperation zwischen  $x(t)$  und  $h_{\rm A}(t)$:

$$y_{\rm A}(t) = x (t) * h_{\rm A} (t) = \int_{ - \infty }^{ + \infty } {x ( \tau )} \cdot h_{\rm A} ( {t - \tau } ) \hspace{0.1cm}{\rm d}\tau.$$

• Aufgrund der Rechteckfunktion und der Dauer  $6T$  kann hierfür auch geschrieben werden:

$$y_{\rm A}(t) = \frac{1}{6T}\cdot \int_{t-6T}^{t}x(\tau)\hspace{0.15cm} {\rm d}\tau.$$

• Man erkennt, dass diese Gleichung für alle  $t$  das gleiche Ergebnis  $y_{\rm A}(t) \rm \underline{\: = 1V}$  liefert.

(2)  Der Betragsfrequenzgang lautet  $|H_{\rm A}(f)| = |{\rm si}(\pi \cdot f \cdot 6T)|.$   Dieser weist Nullstellen im Abstand  $1/(6T)$  auf.

• Somit liegen auch bei  $f_0$,  $3f_0$,  $5f_0$  usw. jeweils Nullstellen vor.
• Insbesondere gilt auch  $|H_{\rm A}(f = f_0)| \underline{\: = 0}$.
• Vom Spektrum  $X(f)$  bleibt somit nur der Gleichanteil  $1 \hspace{0.05cm} \rm V$  unverändert erhalten.
• Dagegen sind alle anderen Spektrallinien in  $Y_{\rm A}(f)$  nicht mehr enthalten.

rechts

(3)  Analog zur Teilaufgabe  (1)  kann man hier für das Ausgangssignal schreiben:

$$y_{\rm B}(t) = \frac{1}{5T}\cdot \int_{t-5T}^{t}x(\tau)\hspace{0.15cm} {\rm d}\tau.$$

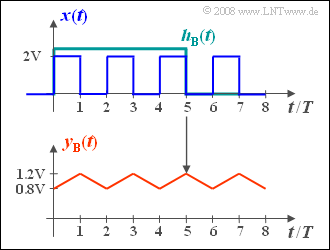
• Es ergibt sich ein um den Mittelwert  $1 \ \rm V$  schwankender dreieckförmiger Verlauf   ⇒   siehe untere Grafik.
• Da jeweils zwei Rechtecke und drei Lücken ins Integrationsintervall fallen, gilt für  $t = 0,  t = 2T,$  usw.:

$$y_{\rm B}(t) = \frac{2\,{\rm V} \cdot 2T }{5T} \hspace{0.15cm}\underline{= 0.8\,{\rm V} =y_{\rm B}(t=0) }.$$

• Bei  $t = T,\ 3T, \ 5T, $  usw. sind jeweils drei Rechtecke und zwei Lücken zu berücksichtigen: Man erhält:

$$y_{\rm B}(t) \underline{\: = 1.2 \: {\rm V}=y_{\rm B}(t=T)}.$$

(4)  Die Betragsfunktion lautet nun allgemein bzw. bei den Frequenzen  $f = f_0 = 1/(2T)$  und  $f = 3f_0$:

$$\begin{align*} |H_{\rm B}(f)| & = |{\rm si}(\pi \cdot f \cdot 5T)|, \\ |H_{\rm B}(f = f_0)| & = |{\rm si}(\pi \frac{5T}{2T})| = |{\rm si}(2.5\pi )| = \frac{1}{2.5 \pi} \hspace{0.15cm}\underline{= 0.127}, \\ |H_{\rm B}(f = 3f_0)| & = |{\rm si}(7.5\pi )| = \frac{1}{7.5 \pi} \hspace{0.15cm}\underline{=0.042}.\end{align*}$$

Interpretation:

• Die Spektralanteile des Rechtecksignals bei  $f_0,  3f_0,$  usw. werden zwar nun nicht mehr unterdrückt, aber mit steigender Frequenz immer mehr abgeschwächt und zwar in der Form, dass der Rechteckverlauf in ein periodisches Dreiecksignal gewandelt wird.   Der Gleichanteil  $(1 \hspace{0.05cm} \rm V)$  bleibt auch hier unverändert.
• Beide Filter liefern also den Mittelwert des Eingangssignals.   Beim vorliegenden Signal  $x(t)$  ist für die Bestimmung des Mittelwertes das Filter  $\rm A$  besser geeignet als das Filter  $\rm B$, da bei Ersterem die Länge der Impulsantwort ein Vielfaches der Periodendauer  $T_0 = 2T$  ist.
• Ist diese Bedingung – wie beim Filter  $\rm B$ – nicht erfüllt, so überlagert sich dem Mittelwert noch ein (in diesem Beispiel dreieckförmiges) Fehlersignal.