Difference between revisions of "Aufgaben:Exercise 2.6Z: Again on the Huffman Code"
| Line 3: | Line 3: | ||
}} | }} | ||
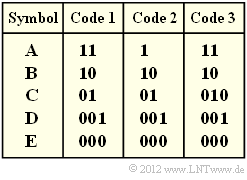
| − | [[File:P_ID2453__Inf_Z_2_6.png|right|frame| | + | [[File:P_ID2453__Inf_Z_2_6.png|right|frame|Three codes to choose from ]] |
| − | + | [https://en.wikipedia.org/wiki/David_A._Huffman David Albert Huffman's] algorithm implements entropy coding with the following properties: | |
| − | * | + | * The resulting binary code is prefix-free and thus easily (and immediately) decodable. |
| − | * | + | * With a memoryless source, the code leads to the smallest possible mean codeword length $L_{\rm M}$. |
| − | * $L_{\rm M}$ | + | * However, $L_{\rm M}$ is never smaller than the source entropy $H$. |
| − | * | + | * These two quantities can be calculated from the $M$ symbol probabilities alone. |
| − | + | For this exercise, we assume a memoryless source with the symbol range $M = 5$ and the alphabet | |
:$$\{ {\rm A},\ {\rm B},\ {\rm C},\ {\rm D},\ {\rm E} \}.$$ | :$$\{ {\rm A},\ {\rm B},\ {\rm C},\ {\rm D},\ {\rm E} \}.$$ | ||
| − | In | + | In the above diagram, three codes are given.nbsp; You are to decide which of these codes were (or could be) created by applying the Huffman algorithm. |
| Line 25: | Line 25: | ||
| − | '' | + | ''Hints:'' |
| − | * | + | *The exercise belongs to the chapter [[Information_Theory/Entropiecodierung_nach_Huffman|Entropy Coding according to Huffman]]. |
| − | * | + | *Further information on the Huffman algorithm can also be found in the information sheet for [[Aufgaben:2.6_Zur_Huffman-Codierung|exercise 2.6]]. |
| − | * | + | *To check your results, please refer to the interaction module [[Applets:Huffman-_und_Shannon-Fano-Codierung|Shannon–Fano– and Huffman–coding]]. |
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Which codes could have arisen according to Huffman for $p_{\rm A} = p_{\rm B} = p_{\rm C} = 0.3$ and $p_{\rm D} = p_{\rm E} = 0.05$ entstanden sein? |
|type="[]"} | |type="[]"} | ||
+ $\text{Code 1}$, | + $\text{Code 1}$, | ||
| Line 42: | Line 42: | ||
| − | { | + | {How are the mean codeword length $L_{\rm M}$ and the entropy $H$ related for the given probabilities? |
|type="()"} | |type="()"} | ||
- $L_{\rm M} < H$, | - $L_{\rm M} < H$, | ||
| Line 49: | Line 49: | ||
| − | { | + | {Consider $\text{code 1}$. With what symbol probabilities would $L_{\rm M} = H$ hold? |
|type="{}"} | |type="{}"} | ||
$\ p_{\rm A} \ = \ $ { 0.25 3% } | $\ p_{\rm A} \ = \ $ { 0.25 3% } | ||
| Line 58: | Line 58: | ||
| − | { | + | {The probabilities calculated in subtask '''(3)''' still apply. <br>However, the mean codeword length is now determined for a sequence of length $N = 40$ ⇒ $L_{\rm M}\hspace{0.03cm}'$. What is possible? |
|type="[]"} | |type="[]"} | ||
+ $L_{\rm M}\hspace{0.01cm}' < L_{\rm M}$, | + $L_{\rm M}\hspace{0.01cm}' < L_{\rm M}$, | ||
| Line 65: | Line 65: | ||
| − | { | + | {Which code could possibly be a Huffman code? |
|type="[]"} | |type="[]"} | ||
+ $\text{Code 1}$, | + $\text{Code 1}$, | ||
| Line 75: | Line 75: | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
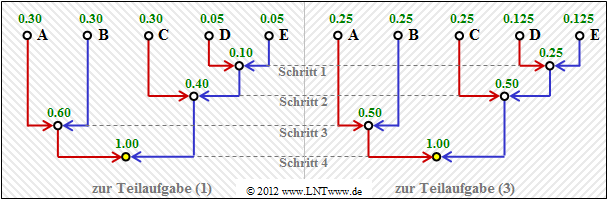
[[File:Inf_Z_2_6a_version2.png|right|frame|Huffman–Baumdiagramme zu den Teilaufgaben '''(1)''' und '''(3)''']] | [[File:Inf_Z_2_6a_version2.png|right|frame|Huffman–Baumdiagramme zu den Teilaufgaben '''(1)''' und '''(3)''']] | ||
Revision as of 21:59, 2 August 2021
David Albert Huffman's algorithm implements entropy coding with the following properties:
- The resulting binary code is prefix-free and thus easily (and immediately) decodable.
- With a memoryless source, the code leads to the smallest possible mean codeword length $L_{\rm M}$.
- However, $L_{\rm M}$ is never smaller than the source entropy $H$.
- These two quantities can be calculated from the $M$ symbol probabilities alone.
For this exercise, we assume a memoryless source with the symbol range $M = 5$ and the alphabet
- $$\{ {\rm A},\ {\rm B},\ {\rm C},\ {\rm D},\ {\rm E} \}.$$
In the above diagram, three codes are given.nbsp; You are to decide which of these codes were (or could be) created by applying the Huffman algorithm.
Hints:
- The exercise belongs to the chapter Entropy Coding according to Huffman.
- Further information on the Huffman algorithm can also be found in the information sheet for exercise 2.6.
- To check your results, please refer to the interaction module Shannon–Fano– and Huffman–coding.
Questions
Solution
(1) Richtig ist der Lösungsvorschlag 1.
- Die Grafik zeigt die Konstruktion des Huffman–Codes mittels Baumdiagramm.
- Mit der Zuordnung rot → 1 und blau → 0 erhält man:
$\rm A$ → 11, $\rm B$ → 10, $\rm C$ → 01, $\rm D$ → 001, $\rm E$ → 000. - Die linke Grafik gilt für die Wahrscheinlichkeiten gemäß Teilaufgabe (1).
- Das rechte Diagramm gehört zur Teilaufgabe (3) mit etwas anderen Wahrscheinlichkeiten.
- Es liefert aber genau den gleichen Code.
(2) Richtig ist der Lösungsvorschlag 3, wie auch die folgende Rechnung zeigt:
- $$L_{\rm M} \hspace{0.2cm} = \hspace{0.2cm} (0.3 + 0.3 + 0.3) \cdot 2 + (0.05 + 0.05) \cdot 3 = 2.1\,{\rm bit/Quellensymbol}\hspace{0.05cm},$$
- $$H \hspace{0.2cm} = \hspace{0.2cm} 3 \cdot 0.3 \cdot {\rm log_2}\hspace{0.15cm}(1/0.3) + 2 \cdot 0.05 \cdot {\rm log_2}\hspace{0.15cm}(1/0.05) \approx 2.0\,{\rm bit/Quellensymbol}\hspace{0.05cm}.$$
- Nach dem Quellencodierungstheorem gilt stets $L_{\rm M} \ge H$.
- Voraussetzung für $L_{\rm M} = H$ ist allerdings, dass alle Symbolwahrscheinlichkeiten in der Form $2^{-k} \ (k = 1, \ 2, \ 3,\ \text{ ...})$ dargestellt werden können.
- Dies trifft hier nicht zu.
(3) $\rm A$, $\rm B$ und $\rm C$ werden beim $\text{Code 1}$ durch zwei Bit dargestellt, $\rm E$ und $\rm F$ durch drei Bit. Damit erhält man für
- die mittlere Codewortlänge
- $$L_{\rm M} = p_{\rm A}\cdot 2 + p_{\rm B}\cdot 2 + p_{\rm C}\cdot 2 + p_{\rm D}\cdot 3 + p_{\rm E}\cdot 3 \hspace{0.05cm},$$
- für die Quellenentropie:
- $$H = p_{\rm A}\cdot {\rm log_2}\hspace{0.15cm}\frac{1}{p_{\rm A}} + p_{\rm B}\cdot {\rm log_2}\hspace{0.15cm}\frac{1}{p_{\rm B}} + p_{\rm C}\cdot {\rm log_2}\hspace{0.15cm}\frac{1}{p_{\rm C}} + p_{\rm D}\cdot {\rm log_2}\hspace{0.15cm}\frac{1}{p_{\rm D}} + p_{\rm E}\cdot {\rm log_2}\hspace{0.15cm}\frac{1}{p_{\rm E}} \hspace{0.05cm}.$$
Durch Vergleich aller Terme kommt man zum Ergebnis:
- $$p_{\rm A}= p_{\rm B}= p_{\rm C}\hspace{0.15cm}\underline{= 0.25} \hspace{0.05cm}, \hspace{0.2cm}p_{\rm D}= p_{\rm E}\hspace{0.15cm}\underline{= 0.125}\hspace{0.3cm} \Rightarrow\hspace{0.3cm} L_{\rm M} = H = 2.25\,{\rm bit/Quellensymbol} \hspace{0.05cm}.$$
Man erkennt:
- Mit diesen "günstigeren" Wahrscheinlichkeiten ergibt sich sogar eine größere mittlere Codewortlänge als mit den "ungünstigeren".
- Die Gleichheit $(L_{\rm M} = H)$ ist demzufolge allein auf die nun größere Quellenentropie zurückzuführen.
(4) Beispielsweise liefert eine (von vielen) Simulationen mit den Wahrscheinlichkeiten gemäß der Teilaufgabe (3) die Folge mit $N = 40$ Zeichen:
- $$\rm EBDCCBDABEBABCCCCCBCAABECAACCBAABBBCDCAB.$$
- Es ergibt sich $L_{\rm M}\hspace{0.01cm}' = ( 34 \cdot 2 + 6 \cdot 3)/50 = 2.15$ bit/Quellensymbol, also ein kleinerer Wert als für die unbegrenzte Folge $(L_{\rm M} = 2.25$ bit/Quellensymbol$)$.
- Bei anderem Startwert des Zufallsgenerators ist aber auch $(L_{\rm M}\hspace{0.03cm}' \ge L_{\rm M})$ möglich.
- Das heißt: Alle Aussagen sind zutreffend.
(5) Richtig ist nur der Lösungsvorschlag 1:
- Der $\text{Code 1}$ ist ein Huffman–Code, wie schon in den vorherigen Teilaufgaben gezeigt wurde.
Dies gilt zwar nicht für alle Symbolwahrscheinlichkeiten, aber zumindest für die Parametersätze gemäß den Teilaufgaben (1) und (3).
- Der $\text{Code 2}$ ist kein Huffman–Code, da ein solcher stets präfixfrei sein müsste.
Die Präfixfreiheit ist hier aber nicht gegeben, da 0 der Beginn des Codewortes 01 ist.
- Der $\text{Code 3}$ ist ebenfalls kein Huffman–Code, da er eine um $p_{\rm C}$ größere mittlere Codewortlänge aufweist als erforderlich $($siehe $\text{Code 1})$. Er ist nicht optimal.
Es gibt keine Symbolwahrscheinlichkeiten $p_{\rm A}$, ... , $p_{\rm E}$, die es rechtfertigen würden, das Symbol $\rm C$ mit 010 anstelle von 01 zu codieren.