Difference between revisions of "Aufgaben:Exercise 2.10: Shannon-Fano Coding"
| Line 3: | Line 3: | ||
}} | }} | ||
| − | [[File:P_ID2465__Inf_A_2_10.png |right|frame| | + | [[File:P_ID2465__Inf_A_2_10.png |right|frame|Tree diagram of the <br>Shannon-Fano coding]] |
Another algorithm for entropy coding was given in 1949 by [https://en.wikipedia.org/wiki/Claude_Shannon Claude Elwood Shannon] and [https://en.wikipedia.org/wiki/Robert_Fano Robert Fano] , which is described in the theory section. | Another algorithm for entropy coding was given in 1949 by [https://en.wikipedia.org/wiki/Claude_Shannon Claude Elwood Shannon] and [https://en.wikipedia.org/wiki/Robert_Fano Robert Fano] , which is described in the theory section. | ||
| Line 65: | Line 65: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {What is the mean codeword length $L_{\rm M}$ for the <u>Huffman code</u>? |
|type="{}"} | |type="{}"} | ||
| − | $L_{\rm M}\ = \ $ { 2.54 3% } $\ \rm bit/ | + | $L_{\rm M}\ = \ $ { 2.54 3% } $\ \rm bit/source\:symbol$ |
| − | { | + | {What happens in the first step of <u>Shannon–Fano coding</u>? ''Hint'': All other symbols are grouped together in the second group. |
|type="[]"} | |type="[]"} | ||
| − | - | + | - $\rm A$ and $\rm B$ are combined into the first group. |
| − | + | + | + $\rm B$ and $\rm E$ are combined into the first group. |
| − | - | + | - The first group consists only of symbol $\rm B$. |
| − | { | + | {Which assignments result for the <u>Shannon–Fano algorithm</u>? |
|type="[]"} | |type="[]"} | ||
| − | + | + | + The character $\rm A$ is binary coded with <b>010</b> . |
| − | + | + | + The character $\rm B$ is binary coded with <b>11</b> . |
| − | + | + | + The character $\rm C$ is binary coded with <b>00110</b> . |
| − | { | + | {What is the average codeword length $L_{\rm M}$ for <u>Shannon–Fano code</u>? |
|type="{}"} | |type="{}"} | ||
| − | $L_{\rm M}\ = \ $ { 2.58 3% } $\ \rm bit/ | + | $L_{\rm M}\ = \ $ { 2.58 3% } $\ \rm bit/source\:symbol$ |
| − | { | + | {Which statements are true for arbitrary probabilities? |
|type="[]"} | |type="[]"} | ||
| − | - $L_{\rm M}$ | + | - $L_{\rm M}$ could be smaller for "Shannon–Fano" than for "Huffman". |
| − | + $L_{\rm M}$ | + | + $L_{\rm M}$ could be larger at "Shannon–Fano" than at "Huffman". |
| − | + $L_{\rm M}$ | + | + $L_{\rm M}$ could be the same for "Shannon–Fano" and "Huffman". |
| Line 99: | Line 99: | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' For the given Huffman code one obtains: |
| − | :$$L_{\rm M} = 0.4 \cdot 1 + (0.17 + 0.14 + 0.10) \cdot 3 + 0.09 \cdot 4 + 0.05 \cdot 5 + (0.03 + 0.02) \cdot 6 =\underline{ 2.54 \,\,{\rm bit/ | + | :$$L_{\rm M} = 0.4 \cdot 1 + (0.17 + 0.14 + 0.10) \cdot 3 + 0.09 \cdot 4 + 0.05 \cdot 5 + (0.03 + 0.02) \cdot 6 =\underline{ 2.54 \,\,{\rm bit/source\:symbol}}\hspace{0.05cm}. $$ |
| − | '''(2)''' | + | '''(2)''' The correct <u>answer is 2</u>: |
| − | * | + | *Before applying the Shannon-Fano algorithm, the characters must first be sorted according to their occurrence probabilities. Thus, answer 1 is incorrect. |
| − | * | + | *All sorted characters must be divided into two groups in such a way that the group probabilities are as equal as possible. For the first step: |
:$${\rm Pr}(\boldsymbol{\rm BE}) = 0.57\hspace{0.05cm}, \hspace{0.2cm}{\rm Pr}(\boldsymbol{\rm DAHGFC}) = 0.43 \hspace{0.05cm}.$$ | :$${\rm Pr}(\boldsymbol{\rm BE}) = 0.57\hspace{0.05cm}, \hspace{0.2cm}{\rm Pr}(\boldsymbol{\rm DAHGFC}) = 0.43 \hspace{0.05cm}.$$ | ||
| − | [[File:P_ID2466__Inf_A_2_10c.png|right|frame| | + | [[File:P_ID2466__Inf_A_2_10c.png|right|frame|Tree diagram of Shannon-Fano coding]] |
| − | * | + | *With the distribution according to solution suggestion 3, the equal distribution would be achieved even less: |
:$${\rm Pr}(\boldsymbol{\rm B}) = 0.40\hspace{0.05cm}, \hspace{0.2cm}{\rm Pr}(\boldsymbol{\rm EDAHGFC}) = 0.60 \hspace{0.05cm}.$$ | :$${\rm Pr}(\boldsymbol{\rm B}) = 0.40\hspace{0.05cm}, \hspace{0.2cm}{\rm Pr}(\boldsymbol{\rm EDAHGFC}) = 0.60 \hspace{0.05cm}.$$ | ||
| Line 118: | Line 118: | ||
| − | '''(3)''' <u> | + | '''(3)''' <u>All suggeted solutionss</u> are correct: |
| − | * | + | *The graph shows the tree diagram of the Shannon-Fano coding. |
| − | * | + | *This results in the following assignment (a red connection indicates a <b>1</b> , a blue one indicates a <b>0</b>): |
: $\underline{\rm A}$ → <u><b>010</b></u>, $\underline{\rm B}$ → <u><b>11</b></u>, $\underline{\rm C}$ → <u><b>00110</b></u>, | : $\underline{\rm A}$ → <u><b>010</b></u>, $\underline{\rm B}$ → <u><b>11</b></u>, $\underline{\rm C}$ → <u><b>00110</b></u>, | ||
: ${\rm D}$ → <b>011</b>, ${\rm E}$ → <b>10</b>, ${\rm F}$ → <b>00111</b>, ${\rm G}$ → <b>0010</b>, ${\rm H}$ → <b>000</b>. | : ${\rm D}$ → <b>011</b>, ${\rm E}$ → <b>10</b>, ${\rm F}$ → <b>00111</b>, ${\rm G}$ → <b>0010</b>, ${\rm H}$ → <b>000</b>. | ||
| Line 126: | Line 126: | ||
| − | '''(4)''' | + | '''(4)''' Using the result of sub-task '''(3)''' , we get: |
| − | :$$L_{\rm M}= (0.40 + 0.17) \cdot 2 + (0.14 + 0.10 + 0.09) \cdot 3 + 0.05 \cdot 4 + (0.03 + 0.02) \cdot 5 =\underline{ 2.58 \,\,{\rm bit/ | + | :$$L_{\rm M}= (0.40 + 0.17) \cdot 2 + (0.14 + 0.10 + 0.09) \cdot 3 + 0.05 \cdot 4 + (0.03 + 0.02) \cdot 5 =\underline{ 2.58 \,\,{\rm bit/source\:symbol}}\hspace{0.05cm}. $$ |
| − | '''(5)''' | + | '''(5)''' <u>Statements 2 and 3</u> are correct: |
| − | * | + | *In the present example, Shannon-Fano results in a less favourable value than Huffman. |
| − | *In | + | *In most cases – including the example on the information page – Huffman and Shannon-Fano result in an equivalent code and thus also the same average code word length. |
| − | * | + | *Shannon-Fano, on the other hand, never delivers a more effective code than Huffman. |
{{ML-Fuß}} | {{ML-Fuß}} | ||
Revision as of 14:44, 6 August 2021
Another algorithm for entropy coding was given in 1949 by Claude Elwood Shannon and Robert Fano , which is described in the theory section.
This special type of source coding will be described here using a simple example for the symbol range $M = 4$ and the following symbol probabilities:
- $$p_{\rm A} = 0.2 \hspace{0.05cm}, \hspace{0.4cm}p_{\rm B}= 0.3 \hspace{0.05cm}, \hspace{0.4cm}p_{\rm C}= 0.4 \hspace{0.05cm},\hspace{0.4cm} p_{\rm D}= 0.1 \hspace{0.05cm}. $$
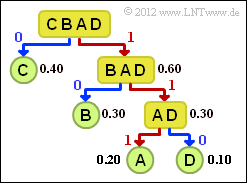
The graph shows the corresponding tree diagram. Proceed as follows:
- 1. Order the symbols according to decreasing probability of occurrence, here $\rm C$ – $\rm B$ – $\rm A$ – $\rm D$.
- 2. Divide the symbols into two groups of approximately equal probability, here $\rm C$ and $\rm BAD$.
- 3. The binary symbol 0is assigned to the less probable group, 1 to the other group.
- 4. If there is more than one symbol in a group, the algorithm is to be applied recursively.
For this example, the following code assignment results (in the tree diagram, a red connection marks a 1 and a blue one a 0:
- $\rm A$ → 111, $\rm B$ → 10, $\rm C$ → 0, $\rm D$ → 110.
This gives the following for the mean codeword length:
- $$L_{\rm M} = 0.4 \cdot 1 + 0.3 \cdot 2 + (0.2 + 0.1) \cdot 3 = 1.9\,\,{\rm bit/source\:symbol}\hspace{0.05cm}.$$
The Huffman algorithm would produce a slightly different code here, but even in this case
- $\rm C$ is coded with one bit,
- $\rm B$ with two bits and
- $\rm A$ and $\rm D$ with three bits each.
This would also result in $L_{\rm M} = 1.9 \ \rm bit/source\:symbol$.
In this task you are to calculate the Shannon-Fano code for $M = 8$ and the probabilities
- $$p_{\rm A} = 0.10 \hspace{0.05cm}, \hspace{0.4cm}p_{\rm B}= 0.40 \hspace{0.05cm}, \hspace{0.4cm}p_{\rm C}= 0.02 \hspace{0.05cm},\hspace{0.4cm} p_{\rm D}= 0.14 \hspace{0.05cm},\hspace{0.4cm} p_{\rm E} = 0.17 \hspace{0.05cm}, \hspace{0.4cm}p_{\rm F}= 0.03 \hspace{0.05cm}, \hspace{0.4cm}p_{\rm G}= 0.05 \hspace{0.05cm},\hspace{0.4cm}p_{\rm H}= 0.09$$
determine. You will see that with these probabilities "Shannon-Fano" will also differ from "Huffman" in terms of efficiency.
With the Huffman code, the following assignment results with the probabilities at hand:
- $\rm A$ → 100, $\rm B$ → 0, $\rm C$ → 111100, $\rm D$ → 101, $\rm E$ → 110, $\rm F$ → 111101, $\rm G$ → 11111, $\rm H$ → 1110.
Hints:
- The assignment belongs to the chapter Other source coding methods.
- In particular, reference is made to the page The Shannon-Fano algorithm.
- To check your results, please refer to the interactive applet Huffman and Shannon-Fano coding.
Questions
Solution
- $$L_{\rm M} = 0.4 \cdot 1 + (0.17 + 0.14 + 0.10) \cdot 3 + 0.09 \cdot 4 + 0.05 \cdot 5 + (0.03 + 0.02) \cdot 6 =\underline{ 2.54 \,\,{\rm bit/source\:symbol}}\hspace{0.05cm}. $$
(2) The correct answer is 2:
- Before applying the Shannon-Fano algorithm, the characters must first be sorted according to their occurrence probabilities. Thus, answer 1 is incorrect.
- All sorted characters must be divided into two groups in such a way that the group probabilities are as equal as possible. For the first step:
- $${\rm Pr}(\boldsymbol{\rm BE}) = 0.57\hspace{0.05cm}, \hspace{0.2cm}{\rm Pr}(\boldsymbol{\rm DAHGFC}) = 0.43 \hspace{0.05cm}.$$
- With the distribution according to solution suggestion 3, the equal distribution would be achieved even less:
- $${\rm Pr}(\boldsymbol{\rm B}) = 0.40\hspace{0.05cm}, \hspace{0.2cm}{\rm Pr}(\boldsymbol{\rm EDAHGFC}) = 0.60 \hspace{0.05cm}.$$
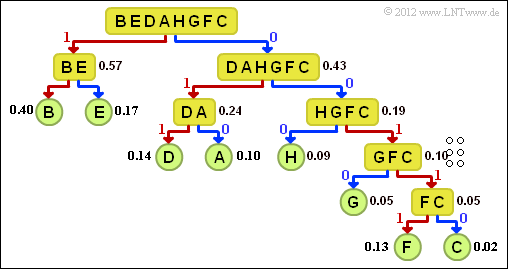
(3) All suggeted solutionss are correct:
- The graph shows the tree diagram of the Shannon-Fano coding.
- This results in the following assignment (a red connection indicates a 1 , a blue one indicates a 0):
- $\underline{\rm A}$ → 010, $\underline{\rm B}$ → 11, $\underline{\rm C}$ → 00110,
- ${\rm D}$ → 011, ${\rm E}$ → 10, ${\rm F}$ → 00111, ${\rm G}$ → 0010, ${\rm H}$ → 000.
(4) Using the result of sub-task (3) , we get:
- $$L_{\rm M}= (0.40 + 0.17) \cdot 2 + (0.14 + 0.10 + 0.09) \cdot 3 + 0.05 \cdot 4 + (0.03 + 0.02) \cdot 5 =\underline{ 2.58 \,\,{\rm bit/source\:symbol}}\hspace{0.05cm}. $$
(5) Statements 2 and 3 are correct:
- In the present example, Shannon-Fano results in a less favourable value than Huffman.
- In most cases – including the example on the information page – Huffman and Shannon-Fano result in an equivalent code and thus also the same average code word length.
- Shannon-Fano, on the other hand, never delivers a more effective code than Huffman.