Difference between revisions of "Aufgaben:Exercise 1.5Z: Symmetrical Markov Source"
From LNTwww
| (17 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Information_Theory/Discrete_Sources_with_Memory |
}} | }} | ||
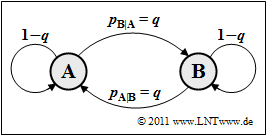
| − | [[File:Inf_Z_1_5_vers2.png|right| | + | [[File:Inf_Z_1_5_vers2.png|right|frame|Binary symmetrical Markov diagram]] |
| − | + | [[Aufgaben:Exercise_1.5:_Binary_Markov_Source|Exercise 1.5]] dealt with a binary Markov source in which the transition probabilities from $\rm A$ to $\rm B$ and from $\rm B$ to $\rm A$ were different. | |
| + | |||
| + | In this task, the following shall now apply: | ||
:$$p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}B} = p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}A} = q \hspace{0.8cm} ( 0 \le q \le 1) | :$$p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}B} = p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}A} = q \hspace{0.8cm} ( 0 \le q \le 1) | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | + | All equations given in Exercise 1.5 also apply here: | |
| − | * <b> | + | * <b>Entropy:</b> |
:$$H = p_{\rm AA} \cdot {\rm log_2}\hspace{0.1cm}\frac {1}{ p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}A}} + p_{\rm AB} \cdot {\rm log_2}\hspace{0.1cm}\frac {1}{ p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}A}} + p_{\rm BA} \cdot {\rm log_2}\hspace{0.1cm}\frac {1}{ p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}B}} + p_{\rm BB} \cdot {\rm log_2}\hspace{0.1cm}\frac {1}{ p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}B}} | :$$H = p_{\rm AA} \cdot {\rm log_2}\hspace{0.1cm}\frac {1}{ p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}A}} + p_{\rm AB} \cdot {\rm log_2}\hspace{0.1cm}\frac {1}{ p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}A}} + p_{\rm BA} \cdot {\rm log_2}\hspace{0.1cm}\frac {1}{ p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}B}} + p_{\rm BB} \cdot {\rm log_2}\hspace{0.1cm}\frac {1}{ p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}B}} | ||
| − | \hspace{0.05cm} | + | \hspace{0.05cm}.$$ |
| − | * <b> | + | * <b>First entropy approximation:</b>: |
:$$H_{\rm 1} = p_{\rm A} \cdot {\rm log_2}\hspace{0.1cm} \frac{1}{p_{\rm A}} + p_{\rm B} \cdot {\rm log_2}\hspace{0.1cm} \frac{1}{p_{\rm B}} | :$$H_{\rm 1} = p_{\rm A} \cdot {\rm log_2}\hspace{0.1cm} \frac{1}{p_{\rm A}} + p_{\rm B} \cdot {\rm log_2}\hspace{0.1cm} \frac{1}{p_{\rm B}} | ||
| − | \hspace{0.05cm} | + | \hspace{0.05cm}.$$ |
| − | * <b><i>k</i>– | + | * <b><i>k</i>–th entropy approximation</b> $(k = 2, 3, \ \text{...})$: |
| − | :$$H_k = {1}/{k} \cdot [ H_{\rm 1} + (k-1) \cdot H] | + | :$$H_k = {1}/{k} \cdot \big [ H_{\rm 1} + (k-1) \cdot H \big] |
\hspace{0.05cm},\hspace{0.5cm}H = \lim_{k \rightarrow \infty } H_k \hspace{0.05cm}.$$ | \hspace{0.05cm},\hspace{0.5cm}H = \lim_{k \rightarrow \infty } H_k \hspace{0.05cm}.$$ | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | === | + | |
| + | |||
| + | |||
| + | ''Hints:'' | ||
| + | *The exercise belongs to the chapter [[Information_Theory/Discrete_Sources_with_Memory|Discrete Sources with Memory]]. | ||
| + | *Reference is made in particular to the page [[Information_Theory/Discrete_Sources_with_Memory#Binary_sources_with_Markov_properties|"Binary sources with Markov properties"]]. | ||
| + | *For all entropies, add the pseudo-unit "bit/symbol". | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | ===Questions=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Calculate the symbol probabilities for the transition probability $q = 1/4$. |
|type="{}"} | |type="{}"} | ||
| − | $p_{\rm A} \ = $ { 0.5 1% } | + | $p_{\rm A} \ = \ $ { 0.5 1% } |
| − | $p_{\rm B} \ = $ { 0.5 1% } | + | $p_{\rm B} \ = \ $ { 0.5 1% } |
| − | { | + | {Calculate the source entropy $H$ for $q = 1/4$. |
|type="{}"} | |type="{}"} | ||
| − | $H \ =$ { 0. | + | $H \ =$ { 0.811 3% } $\ \rm bit/symbol$ |
| − | { | + | {What entropy approximations are obtained for $q = 1/4$? |
|type="{}"} | |type="{}"} | ||
| − | $H_1 \ =$ { 1 1% } $\ \rm bit/ | + | $H_1 \ = \ $ { 1 1% } $\ \rm bit/symbol$ |
| − | $H_2 \ =$ { 0.906 1% } $\ \rm bit/ | + | $H_2 \ = \ $ { 0.906 1% } $\ \rm bit/symbol$ |
| − | $H_3 \ =$ { 0.874 1% } $\ \rm bit/ | + | $H_3 \ = \ $ { 0.874 1% } $\ \rm bit/symbol$ |
| − | { | + | {Determine $q$ such that $H$ becomes maximum. Interpretation. |
|type="{}"} | |type="{}"} | ||
| − | $ | + | $q \ = \ $ { 0.5 3% } |
| − | { | + | {Which symbol sequences are possible with $q = 0$ ? |
|type="[]"} | |type="[]"} | ||
+ $\rm AAAAAA$ ... | + $\rm AAAAAA$ ... | ||
| Line 63: | Line 71: | ||
| − | { | + | {Which symbol sequences are possible with $q = 1$ ? |
|type="[]"} | |type="[]"} | ||
- $\rm AAAAAA$ ... | - $\rm AAAAAA$ ... | ||
| Line 73: | Line 81: | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' For a stationary first order binary Markov source holds: |
:$$p_{\rm A} = p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}A} \cdot p_{\rm A} + p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}B} \cdot p_{\rm B} | :$$p_{\rm A} = p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}A} \cdot p_{\rm A} + p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}B} \cdot p_{\rm B} | ||
= (1-q) \cdot p_{\rm A} + q \cdot p_{\rm B}$$ | = (1-q) \cdot p_{\rm A} + q \cdot p_{\rm B}$$ | ||
| − | :$$q \cdot p_{\rm A} = q \cdot p_{\rm B} \hspace{0.3cm} \Rightarrow \hspace{0.3cm}p_{\rm A} = p_{\rm B}\hspace{0.15cm} \underline {= 0.5} | + | :$$\Rightarrow \hspace{0.3cm}q \cdot p_{\rm A} = q \cdot p_{\rm B} \hspace{0.3cm} \Rightarrow \hspace{0.3cm}p_{\rm A} = p_{\rm B}\hspace{0.15cm} \underline {= 0.5} |
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | '''(2)''' | + | |
| + | |||
| + | '''(2)''' To calculate the entropy $H$ one needs all four composite probabilities: | ||
:$$p_{\rm AA} \hspace{0.1cm} = \hspace{0.1cm} p_{\rm A} \cdot p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}A} = 1/2 \cdot(1-q) = p_{\rm BB}\hspace{0.05cm},\hspace{1cm} | :$$p_{\rm AA} \hspace{0.1cm} = \hspace{0.1cm} p_{\rm A} \cdot p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}A} = 1/2 \cdot(1-q) = p_{\rm BB}\hspace{0.05cm},\hspace{1cm} | ||
p_{\rm AB} \hspace{0.1cm} = \hspace{0.1cm} p_{\rm A} \cdot p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}A} = 1/2 \cdot q = p_{\rm BA}\hspace{0.05cm}.$$ | p_{\rm AB} \hspace{0.1cm} = \hspace{0.1cm} p_{\rm A} \cdot p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}A} = 1/2 \cdot q = p_{\rm BA}\hspace{0.05cm}.$$ | ||
| − | + | *Substituting these values into the given entropy equation, we get | |
:$$H = 2 \cdot \frac{1}{2} \cdot(1-q) \cdot | :$$H = 2 \cdot \frac{1}{2} \cdot(1-q) \cdot | ||
{\rm log}_2\hspace{0.1cm} \frac{1}{1-q} + 2 \cdot \frac{1}{2} \cdot q \cdot | {\rm log}_2\hspace{0.1cm} \frac{1}{1-q} + 2 \cdot \frac{1}{2} \cdot q \cdot | ||
{\rm log}_2\hspace{0.1cm} \frac{1}{q} = q \cdot {\rm log}_2\hspace{0.1cm} \frac{1}{q} + (1-q) \cdot {\rm log}_2\hspace{0.1cm} \frac{1}{1-q} = H_{\rm bin}(q) \hspace{0.05cm}.$$ | {\rm log}_2\hspace{0.1cm} \frac{1}{q} = q \cdot {\rm log}_2\hspace{0.1cm} \frac{1}{q} + (1-q) \cdot {\rm log}_2\hspace{0.1cm} \frac{1}{1-q} = H_{\rm bin}(q) \hspace{0.05cm}.$$ | ||
| − | + | *The numerical value sought is $H = H_{\rm bin} (0.25) \hspace{0.15cm}\underline{= 0.811 \, \rm bit/symbol}$. | |
| − | '''(3)''' | + | |
| − | :$$H_2 \hspace{0.1cm} = \hspace{0.1cm} {1}/{2} \cdot [ H_1 + H] \hspace{0.15cm} \underline {= 0.906 \,{\rm bit/Symbol}} | + | '''(3)''' For equally probable binary symbols, $H_1 \hspace{0.15cm}\underline{= 1 \, \rm bit/Symbol}$. |
| + | *Using the equation valid for Markov sources, it further holds: | ||
| + | :$$H_2 \hspace{0.1cm} = \hspace{0.1cm} {1}/{2} \cdot \big[ H_1 + H \big] \hspace{0.15cm} \underline {= 0.906 \,{\rm bit/Symbol}} | ||
\hspace{0.05cm},$$ | \hspace{0.05cm},$$ | ||
| − | :$$ H_3 \hspace{0.1cm} = \hspace{0.1cm} {1}/{3} \cdot [ H_1 + 2 H] \hspace{0.15cm} \underline {= 0.874 \,{\rm bit/Symbol}} | + | :$$ H_3 \hspace{0.1cm} = \hspace{0.1cm} {1}/{3} \cdot \big[ H_1 + 2 H \big] \hspace{0.15cm} \underline {= 0.874 \,{\rm bit/Symbol}} |
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | '''(4)''' | + | |
| + | '''(4)''' The maximum of the binary entropy function is obtained for $q\hspace{0.15cm}\underline{= 0.5}$. | ||
| + | *Thus the maximum entropy is $H = 1 \, \rm bit/symbol$. | ||
| + | *It can be seen from the relationship $H = H_1$ and from the transition diagram shown at the front that $q = 0.5$ results in statistically independent symbols: | ||
:$$p_{\rm A} = p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}A} = p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}B} = 0.5 | :$$p_{\rm A} = p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}A} = p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}B} = 0.5 | ||
\hspace{0.05cm}, \hspace{0.2cm} p_{\rm B} = p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}A} = p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}B}= 0.5 | \hspace{0.05cm}, \hspace{0.2cm} p_{\rm B} = p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}A} = p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}B}= 0.5 | ||
| Line 104: | Line 119: | ||
| − | '''(5)''' | + | |
| − | * | + | '''(5)''' <u>Proposed solutions 1 and 2</u> are correct: |
| − | * | + | *The symbol sequence results either in $\rm AAAAAA$ ... or in $\rm BBBBBB$ ... , depending on which symbol was given as the starting value. |
| + | *The entropy of such a source is always $H = H_{\rm bin}(0) = 0$. | ||
| + | |||
| + | |||
| − | '''(6)''' | + | '''(6)''' Only <u>proposed solution 3</u> is correct: |
| − | * | + | *Now neither $\rm A$ can directly follow $\rm A$ nor $\rm B$ can directly follow $\rm B$ . |
| − | * | + | *The result is always an alternating sequence, depending on the starting value the sequence $\rm ABABAB$ ... or $\rm BABABA$... . |
| − | * | + | *This source also has the entropy $H = H_{\rm bin}(1) = 0$ in both cases. |
{{ML-Fuß}} | {{ML-Fuß}} | ||
| − | [[Category: | + | [[Category:Information Theory: Exercises|^1.2 Sources with Memory^]] |
Latest revision as of 13:04, 10 August 2021
Exercise 1.5 dealt with a binary Markov source in which the transition probabilities from $\rm A$ to $\rm B$ and from $\rm B$ to $\rm A$ were different.
In this task, the following shall now apply:
- $$p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}B} = p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}A} = q \hspace{0.8cm} ( 0 \le q \le 1) \hspace{0.05cm}.$$
All equations given in Exercise 1.5 also apply here:
- Entropy:
- $$H = p_{\rm AA} \cdot {\rm log_2}\hspace{0.1cm}\frac {1}{ p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}A}} + p_{\rm AB} \cdot {\rm log_2}\hspace{0.1cm}\frac {1}{ p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}A}} + p_{\rm BA} \cdot {\rm log_2}\hspace{0.1cm}\frac {1}{ p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}B}} + p_{\rm BB} \cdot {\rm log_2}\hspace{0.1cm}\frac {1}{ p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}B}} \hspace{0.05cm}.$$
- First entropy approximation::
- $$H_{\rm 1} = p_{\rm A} \cdot {\rm log_2}\hspace{0.1cm} \frac{1}{p_{\rm A}} + p_{\rm B} \cdot {\rm log_2}\hspace{0.1cm} \frac{1}{p_{\rm B}} \hspace{0.05cm}.$$
- k–th entropy approximation $(k = 2, 3, \ \text{...})$:
- $$H_k = {1}/{k} \cdot \big [ H_{\rm 1} + (k-1) \cdot H \big] \hspace{0.05cm},\hspace{0.5cm}H = \lim_{k \rightarrow \infty } H_k \hspace{0.05cm}.$$
Hints:
- The exercise belongs to the chapter Discrete Sources with Memory.
- Reference is made in particular to the page "Binary sources with Markov properties".
- For all entropies, add the pseudo-unit "bit/symbol".
Questions
Solution
(1) For a stationary first order binary Markov source holds:
- $$p_{\rm A} = p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}A} \cdot p_{\rm A} + p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}B} \cdot p_{\rm B} = (1-q) \cdot p_{\rm A} + q \cdot p_{\rm B}$$
- $$\Rightarrow \hspace{0.3cm}q \cdot p_{\rm A} = q \cdot p_{\rm B} \hspace{0.3cm} \Rightarrow \hspace{0.3cm}p_{\rm A} = p_{\rm B}\hspace{0.15cm} \underline {= 0.5} \hspace{0.05cm}.$$
(2) To calculate the entropy $H$ one needs all four composite probabilities:
- $$p_{\rm AA} \hspace{0.1cm} = \hspace{0.1cm} p_{\rm A} \cdot p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}A} = 1/2 \cdot(1-q) = p_{\rm BB}\hspace{0.05cm},\hspace{1cm} p_{\rm AB} \hspace{0.1cm} = \hspace{0.1cm} p_{\rm A} \cdot p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}A} = 1/2 \cdot q = p_{\rm BA}\hspace{0.05cm}.$$
- Substituting these values into the given entropy equation, we get
- $$H = 2 \cdot \frac{1}{2} \cdot(1-q) \cdot {\rm log}_2\hspace{0.1cm} \frac{1}{1-q} + 2 \cdot \frac{1}{2} \cdot q \cdot {\rm log}_2\hspace{0.1cm} \frac{1}{q} = q \cdot {\rm log}_2\hspace{0.1cm} \frac{1}{q} + (1-q) \cdot {\rm log}_2\hspace{0.1cm} \frac{1}{1-q} = H_{\rm bin}(q) \hspace{0.05cm}.$$
- The numerical value sought is $H = H_{\rm bin} (0.25) \hspace{0.15cm}\underline{= 0.811 \, \rm bit/symbol}$.
(3) For equally probable binary symbols, $H_1 \hspace{0.15cm}\underline{= 1 \, \rm bit/Symbol}$.
- Using the equation valid for Markov sources, it further holds:
- $$H_2 \hspace{0.1cm} = \hspace{0.1cm} {1}/{2} \cdot \big[ H_1 + H \big] \hspace{0.15cm} \underline {= 0.906 \,{\rm bit/Symbol}} \hspace{0.05cm},$$
- $$ H_3 \hspace{0.1cm} = \hspace{0.1cm} {1}/{3} \cdot \big[ H_1 + 2 H \big] \hspace{0.15cm} \underline {= 0.874 \,{\rm bit/Symbol}} \hspace{0.05cm}.$$
(4) The maximum of the binary entropy function is obtained for $q\hspace{0.15cm}\underline{= 0.5}$.
- Thus the maximum entropy is $H = 1 \, \rm bit/symbol$.
- It can be seen from the relationship $H = H_1$ and from the transition diagram shown at the front that $q = 0.5$ results in statistically independent symbols:
- $$p_{\rm A} = p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}A} = p_{\rm A\hspace{0.01cm}|\hspace{0.01cm}B} = 0.5 \hspace{0.05cm}, \hspace{0.2cm} p_{\rm B} = p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}A} = p_{\rm B\hspace{0.01cm}|\hspace{0.01cm}B}= 0.5 \hspace{0.05cm}.$$
(5) Proposed solutions 1 and 2 are correct:
- The symbol sequence results either in $\rm AAAAAA$ ... or in $\rm BBBBBB$ ... , depending on which symbol was given as the starting value.
- The entropy of such a source is always $H = H_{\rm bin}(0) = 0$.
(6) Only proposed solution 3 is correct:
- Now neither $\rm A$ can directly follow $\rm A$ nor $\rm B$ can directly follow $\rm B$ .
- The result is always an alternating sequence, depending on the starting value the sequence $\rm ABABAB$ ... or $\rm BABABA$... .
- This source also has the entropy $H = H_{\rm bin}(1) = 0$ in both cases.