Exercise 2.12: Run–Length Coding and Run–Length Limited Coding

• Return to book

Table on Run-Length Coding

We consider a binary source with the symbol set  $\rm A$  and  $\rm B$, where  $\rm B$  however, occurs only very rarely.

• Without source coding, exactly one bit would be needed per source symbol, and accordingly, for a source symbol sequence of length  $N$  would also apply to the coder symbol sequence  $N_\text{bits} = N$.
• Entropy coding makes little sense here without further measures  (example:  combining several symbols into a tuple)  because of the unfavourable symbol probabilities.
• The remedy is  Run-Length Coding  $(\rm RLC)$, which is described in the theory section under the link mentioned.  For example, for the symbol sequence   $\rm ABAABAAAABBAAB\text{...}$   the corresponding output of  "Run–Length Coding":   $2; \ 3; \ 5; \ 1; \ 3; \text{...}$
• Of course, the lengths  $L_1 = 2$,  $L_2 = 3$, ...  of the individual substrings, each separated by  $\rm B$ , must be represented in binary before transmission.  If one uses  $D = 3$  (bit) for all  $L_i$  one obtains the RLC binary symbol sequence

$$010\hspace{0.05cm}\text{'}\hspace{0.05cm}011\hspace{0.05cm}\text{'}\hspace{0.05cm}101\hspace{0.05cm}\text{'}\hspace{0.05cm}001\hspace{0.05cm}\text{'}\hspace{0.05cm}011\hspace{0.05cm}\text{'}\hspace{0.05cm}\text{...}$$

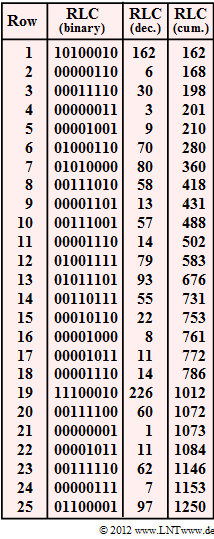
The graph shows the RLC result to be analysed.  Columns 2 and 3 show the substring lengths  $L_i$  in binary and decimal, respectively, and column 4 shows them in cumulative form  (values from column 3 added up).

• One problem of  "Run-Length Coding"  $\rm (RLC)$ is the unlimited range of values of the quantities  $L_i$.  With  $D = 3$,  no value  $L_i > 7$  can be represented and with  $D = 2$,  the restriction is  $1 \le L_i \le 3$.

• The problem is circumvented with  "Run–Length Limited Coding"  $\rm (RLLC)$.  If a value is  $L_i \ge 2^D$,  one replaces  $L_i$  with a special character  S  and the difference  $L_i - 2^D +1$.  With the RLLC decoder, this special character  S  is expanded again.

Hints:

• This exercise belongs to the chapter  Further source coding methods.
• In particular, reference is made to the page  Run-Length Coding.

$\text{RLLC Example}$:  We again assume the above sequence and the parameter  $D = 2$ :

• Source symbol sequence:    $\rm ABAABAAAABBAAB$...
• RLC decimal sequence:          2; 3; 5; 1; 3; ...
• RLLC decimal sequence:       2;  3;  S; 2;  1;  3; ...
• RLLC binary sequence:          10′11′ 00′10′01′11′...

You can see:

• The special character  S  is binary-coded here as  00 .  This is only an example – it does not have to be like this.
• Since with  $D = 2$  for all real RLC values  $1 \le L_i \le 3$ , the decoder recognizes the special character  00.
• It replaces this again with  $2^D -1$  (three in the example)  $\rm A$–symbols.

Questions

1

How many bits would be needed  without source coding , i.e. with the assignment  $\rm A$   →  0  and  $\rm B$   →  1?

$N_\text{Bit} \ = \ $

2

What is the relative frequency of symbol  $\rm B$?

$h_{\rm B}\ = \ $ $\ \%$

3

How many bits are needed for  Run–Length Coding  $\rm (RLC)$  according to the given table with eight bits per codeword  $(D = 8)$?

$N_\text{Bit} \ = \ $

4

Is  Run–Length Coding  with seven bit code words  $(D = 7)$  possible here?

	Yes.
	No.

5

How many bits are needed for  Run–Length Limited Coding  $\rm (RLLC)$  with seven bits per code word  $(D = 7)$?

$N_\text{Bit} \ = \ $

6

How many bits are needed for  Run–Length Limited Coding  $\rm (RLLC)$  with six bits per codeword  $(D = 6)$?

$N_\text{Bit} \ = \ $

Solution

Solution

(1)  The binary sequence consists of  $N = 1250$  binary symbols (can be read from the last column in the table).  This means that the same number of bits is needed without coding:

$$N_\text{Bit}\hspace{0.15cm}\underline{= 1250}.$$

(2)  The entire symbol sequence of length  $N = 1250$  contains  $N_{\rm B} = 25$  symbols  ${\rm B}$  and thus  $N_{\rm A} = 1225$  symbols  ${\rm A}$. 

• The number  $N_{\rm B}$  der Symbole  ${\rm B}$  ist dabei gleich der Zeilenzahl in der vorne angegebenen Tabelle.
• Thus the following applies to the relative frequency of   ${\rm B}$:

$$h_{\rm B} = \frac{N_{\rm B}}{N} = \frac{25}{1250} \hspace{0.15cm}\underline{= 0.02} = 2\%\hspace{0.05cm}.$$

(3)  We now consider  Run–Length Coding  $\rm (RLC)$, where each distance between two  ${\rm B}$–symbols is represented by eight bits  $(D = 8)$.

• Thus, with  $N_{\rm B} = 25$, we get::

$$N_{\rm Bit} = N_{\rm B} \cdot 8 \hspace{0.15cm}\underline{= 200} \hspace{0.05cm}.$$

(4)  $\rm RLC$  with  $D = 7$ only allows values between  $1$  und  $2^7-1 =127$ for  $L_i$  .

• However, the entry "226" in line 19 is greater     ⇒     NO.

(5)  Even with Run–Length Limited Coding  $\rm (RLLC)$  , only values up to  $127$&nbsp are permitted for the "real" distances  $L_i$  with  $D = 7$  ;.

• The entry "226" in line 19 is replaced by the following for  $\rm RLLC$ 

• Line 19a:   S = 0000000   ⇒   special character, stands for "+ 127",

• Line 19b:   1100011   ⇒   decimal 99.

• This gives a total of $26$ words of seven bits each:

$$N_{\rm Bit} = 26 \cdot 7 \hspace{0.15cm}\underline{= 182} \hspace{0.05cm}.$$

(6)  Now the following changes have to be made in  $\rm RLLC$  compared to  $\rm RLC$  (see table):

• Zeile   1:   $122 = 1 · 63 + 59$   (one word more),

• Zeile   6:     $70 = 1 · 63 + 7$     (one word more),

• Zeile   7:     $80 = 1 · 63 + 17$   (one word more),

• Zeile 12:     $79 = 1 · 63 + 18$   (one word more),

• Zeile 13:     $93 = 1 · 63 + 30$   (one word more),

• Zeile 19:   $226 = 3 · 63 + 37$   (one word more),

• Zeile 25:     $97 = 1 · 63 + 34$   (one word more).

This gives a total of $34$ words of six bits each:

$$N_{\rm Bit} = 34 \cdot 6 \hspace{0.15cm}\underline{= 204} \hspace{0.05cm},$$

i.e. a worse result than with seven bits according to subtask (5).