Difference between revisions of "Aufgaben:Exercise 2.11: Arithmetic Coding"
| (24 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Information_Theory/Further_Source_Coding_Methods |
}} | }} | ||
| − | [[File: | + | [[File:EN_Inf_A_2_11_v3.png|right|frame|Interval nesting for arithmetic coding]] |
| − | + | Arithmetic coding is a special form of entropy coding: The symbol probabilities must also be known here. | |
| − | + | In this exercise, we assume $M = 3$ symbols, which we name with $\rm X$, $\rm Y$ and $\rm Z$. | |
| − | :$$I = [B, E) = [B, B +{\it \Delta} )\hspace{0.05cm}.$$ | + | While Huffman coding is done symbol by symbol, in Arithmetic Coding $(\rm AC)$ a sequence of symbols of length $N$ is encoded together. The coding result is a real numerical value $r$ from the interval |
| − | + | :$$I = \big[B, \ E \big) = \big[B, \ B +{\it \Delta} \big)\hspace{0.05cm}.$$ | |
| − | * | + | This notation means: |
| − | * | + | * The beginning $B$ belongs to the interval $I$. |
| − | * | + | * The end $E$ is no longer contained in $I$ . |
| + | * The interval width is ${\it} {\it \Delta} = E - B$. | ||
| − | + | ||
| − | * | + | Of the infinite number of possible values $r \in I$ $($since $r$ is real-valued, i.e. not an integer$)$, the numerical value that gets by with the smallest number of bits is selected. Here are two examples for clarification: |
| + | * The decimal value $r = 3/4$ can be represented with two bits: | ||
:$$r = 1 \cdot 2^{-1} + 1 \cdot 2^{-2} = 0.75 \hspace{0.3cm} | :$$r = 1 \cdot 2^{-1} + 1 \cdot 2^{-2} = 0.75 \hspace{0.3cm} | ||
| − | \Rightarrow\hspace{0.3cm}\text{ | + | \Rightarrow\hspace{0.3cm}\text{binary:}\hspace{0.25cm} 0.11\hspace{0.3cm}\Rightarrow\hspace{0.3cm}\text |
| − | {Code:} \hspace{0. | + | {Code:} \hspace{0.25cm} \boldsymbol{\rm 11} \hspace{0.05cm}, $$ |
| − | * | + | * The decimal value $r = 1/3$ , on the other hand, requires an infinite number of bits: |
:$$r = 0 \cdot 2^{-1} + 1 \cdot 2^{-2} + 1 \cdot 2^{-3}+ 1 \cdot 2^{-4}+ 0 \cdot 2^{-5} + 1 \cdot 2^{-6} + \hspace{0.05cm}\text{...}$$ | :$$r = 0 \cdot 2^{-1} + 1 \cdot 2^{-2} + 1 \cdot 2^{-3}+ 1 \cdot 2^{-4}+ 0 \cdot 2^{-5} + 1 \cdot 2^{-6} + \hspace{0.05cm}\text{...}$$ | ||
:$$ | :$$ | ||
| − | \Rightarrow\hspace{0.3cm}\text{binär:} \hspace{0. | + | \Rightarrow\hspace{0.3cm}\text{binär:} \hspace{0.25cm}0.011101\hspace{0.05cm}\text{...}\hspace{0.3cm}\Rightarrow\hspace{0.3cm} |
| − | \text{Code:} \hspace{0. | + | \text{Code:} \hspace{0.25cm} \boldsymbol{\rm 011101}\hspace{0.05cm}\text{...} \hspace{0.05cm}. $$ |
| − | In | + | In this task we restrict ourselves to the determination of the current interval $I$, marked by the beginning $B$ as well as the end $E$ and the width ${\it \Delta}$ respectively. |
| + | *This determination is done according to the interval nesting in the above diagram. | ||
| + | *The hatching shows that the sequence begins with the ternary symbols $\rm XXY$ . | ||
| + | <br clear=all> | ||
| + | The algorithm works as follows: | ||
| + | * Before the beginning (quasi at the zero symbol) the entire probability range is divided into three areas according to the probabilities $p_{\rm X}$, $p_{\rm Y}$ and $p_{\rm Z}$ . The limits are | ||
| + | :$$B_0 = 0\hspace{0.05cm},\hspace{0.4cm}C_0 = p_{\rm X}\hspace{0.05cm},\hspace{0.4cm}D_0 = p_{\rm X} + p_{\rm Y}\hspace{0.05cm},\hspace{0.4cm} E_0 = p_{\rm X} + p_{\rm Y}+ p_{\rm Z} = 1\hspace{0.05cm}.$$ | ||
| − | + | * The first symbol of the sequence to be coded is $\rm X$. This means: The selected interval is limited by $B_0$ and $C_0$ . | |
| − | * | + | *This interval is divided with new beginning $B_1 = B_0$ and new end $E_1 = C_0$ in the same way as the total range in the zero step. <br>The intermediate values are $C_1$ and $D_1$. |
| − | + | * The further interval division is your task. For example, in subtask '''(2)''' the boundaries $B_2$, $C_2$, $D_2$ and $E_2$ for the second symbol $\rm X$ are to be determined <br>and in subtask '''(3)''' the boundaries $B_3$, $C_3$, $D_3$ and $E_3$ for the third symbol $\rm Y$ are to be determined. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | === | + | <u>Hints:</u> |
| + | *The exercise belongs to the chapter [[Information_Theory/Further_Source_Coding_Methods|Further source coding methods]]. | ||
| + | *In particular, reference is made to the page [[Information_Theory/Further_Source_Coding_Methods#Arithmetic_coding|Arithmetic Coding]]. | ||
| + | *The binary representation of the selected interval is dealt with in [[Aufgaben:Exercise_2.11Z:_Arithmetic_Coding_once_again|Exercise 2.11Z]]. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | ===Questions=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {What are the underlying probabilities of the graph? |
|type="{}"} | |type="{}"} | ||
| − | $p_{\rm X} \ = \ $ { 0.7 3% } | + | $p_{\rm X} \hspace{0.10cm} = \ $ { 0.7 3% } |
| − | $p_{\rm Y} \ = \ $ { 0.1 3% } | + | $p_{\rm Y} \hspace{0.10cm} = \ $ { 0.1 3% } |
| − | $p_{\rm Z} \ = \ $ { 0.2 3% } | + | $p_{\rm Z} \hspace{0.15cm} = \ $ { 0.2 3% } |
| − | { | + | {What are the range limits after coding the second symbol $\rm X$? |
|type="{}"} | |type="{}"} | ||
| − | $B_2 \ = \ $ { 0. } | + | $B_2 \hspace{0.12cm} = \ $ { 0. } |
| − | $C_2 \ = \ ${ 0.343 | + | $C_2 \hspace{0.15cm} = \ $ { 0.343 1% } |
| − | $D_2 \ = \ $ { 0.392 | + | $D_2 \hspace{0.10cm} = \ $ { 0.392 1% } |
| − | $E_2 \ = \ $ { 0.49 | + | $E_2 \hspace{0.15cm} = \ $ { 0.49 1% } |
| − | { | + | {What are the range limits after coding the third symbol $\rm Y$? |
|type="{}"} | |type="{}"} | ||
| − | $B_3 \ = \ $ { 0.343 | + | $B_3 \hspace{0.12cm} = \ $ { 0.343 1% } |
| − | $C_3 \ = \ $ { 0.3773 | + | $C_3 \hspace{0.15cm} = \ $ { 0.3773 1% } |
| − | $D_3 \ = \ $ { 0.3822 | + | $D_3 \hspace{0.10cm} = \ $ { 0.3822 1% } |
| − | $E_3 \ = \ $ { 0.392 | + | $E_3 \hspace{0.15cm} = \ $ { 0.392 1% } |
| − | { | + | {After coding the fourth symbol, $B_4 = 0.343$. What follows from this? |
| − | |type=" | + | |type="()"} |
| − | + | + | + The fourth symbol was $\rm X$. |
| − | - | + | - The fourth symbol was $\rm Y$. |
| − | - | + | - The fourth symbol was $\rm Z$. |
| + | |||
| + | {After more symbols, the interval is bounded by $B_7 = 0.3564456$ and $E_7 = 0.359807$ . Which statements are true? | ||
| − | |||
|type="[]"} | |type="[]"} | ||
| − | - | + | - The symbol sequence to be encoded is $\rm XXYXXZX$. |
| − | + | + | + The symbol sequence to be encoded is $\rm XXYXXXZ$. |
| − | + | + | + The width of the resulting interval is ${\it \Delta} = p_{\rm X}^5 \cdot p_{\rm Y} \cdot p_{\rm Z}$. |
| − | { | + | {Which real numbers (in binary form) fall into the selected interval? |
|type="[]"} | |type="[]"} | ||
| − | - $r_1 = (0.101100)_{\text{ | + | - $r_1 = (0.101100)_{\text{binary}}$, |
| − | + $r_2 = (0.010111)_{\text{ | + | + $r_2 = (0.010111)_{\text{binary}}$, |
| − | - $r_3 = (0.001011)_{\text{ | + | - $r_3 = (0.001011)_{\text{binary}}$. |
| Line 91: | Line 101: | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
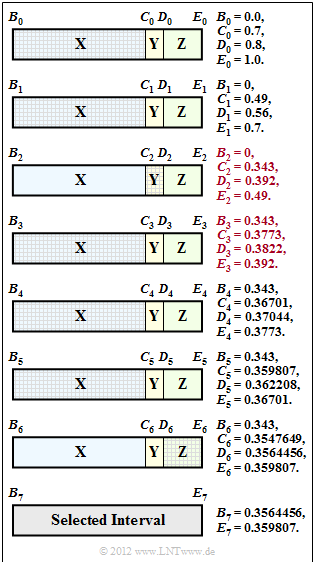
| − | [[File: | + | [[File:EN_Inf_A_2_11_ML_vers2.png|right|frame|Interval nesting with all numerical values]] |
| − | + | '''(1)''' From the graph on the information page you can read the probabilities: | |
:$$p_{\rm X} = 0.7\hspace{0.05cm},\hspace{0.2cm}p_{\rm Y} = 0.1\hspace{0.05cm},\hspace{0.2cm}p_{\rm Z} = 0.2\hspace{0.05cm}.$$ | :$$p_{\rm X} = 0.7\hspace{0.05cm},\hspace{0.2cm}p_{\rm Y} = 0.1\hspace{0.05cm},\hspace{0.2cm}p_{\rm Z} = 0.2\hspace{0.05cm}.$$ | ||
| − | |||
| − | |||
| − | |||
| − | + | '''(2)''' The second symbol is also $\rm X$. Using the same procedure as in the task description, we get | |
| − | :$$B_3 \hspace{0.1cm}\underline{= 0.343}\hspace{0.05cm},\hspace{0.2cm}C_3 \hspace{0.1cm}\underline{= 0.3773}\hspace{0.05cm}, | + | :$$B_2 \hspace{0.1cm}\underline{= 0}\hspace{0.05cm},\hspace{0.2cm}C_2 = 0.49 \cdot 0.7 \hspace{0.1cm}\underline{= 0.343}\hspace{0.05cm},\hspace{0.2cm} |
| − | + | D_2 \hspace{0.1cm} \underline{= 0.392}\hspace{0.05cm},\hspace{0.2cm}E_2 = C_1 \hspace{0.1cm}\underline{= 0.49} \hspace{0.05cm}.$$ | |
| + | |||
| + | |||
| + | '''(3)''' For the third symbol $\rm Y$ the limitations $B_3 = C_2$ and $E_3 = D_2$ now apply: | ||
| + | :$$B_3 \hspace{0.1cm}\underline{= 0.343}\hspace{0.05cm},\hspace{0.2cm}C_3 \hspace{0.1cm}\underline{= 0.3773}\hspace{0.05cm},\hspace{0.2cm} | ||
| + | D_3 \hspace{0.1cm} \underline{= 0.3822}\hspace{0.05cm},\hspace{0.2cm}E_3 \hspace{0.1cm}\underline{= 0.392} \hspace{0.05cm}.$$ | ||
| − | |||
| − | < | + | '''(4)''' <u>Solution suggestion 1</u> is correct: |
| + | *From $B_4 = 0.343 = B_3$ (to be read in the diagram on the data sheet) it follows that the fourth source symbol was an $\rm X$. | ||
| − | |||
| − | :* | + | '''(5)''' <u>Proposed solutions 2 and 3</u> are correct: |
| − | :$${\it \Delta} | + | *The graph shows the interval nesting with all previous results. You can see from the hatching that the second suggested solution gives the correct sequence of symbols: $\rm XXYXXXZ$. |
| − | + | * The interval width $\it \Delta$ can really be determined according to suggestion 3. It holds: | |
| + | :$${\it \Delta} = 0.359807 - 0.3564456 = 0.003614 \hspace{0.05cm},$$ | ||
| + | :$$\Rightarrow \hspace{0.3cm} {\it \Delta} =p_{\rm X}^5 \cdot p_{\rm Y} \cdot p_{\rm Z} = 0.7^5 \cdot 0.1 \cdot 0.2 = 0.003614 | ||
\hspace{0.05cm}. $$ | \hspace{0.05cm}. $$ | ||
| − | |||
| − | < | + | '''(6)''' Correct is the <u>proposed solution 2</u> ⇒ $r_2 = (0.010111)_{\text{binary}}$, because of: |
| + | :$$r_2 = 0 \cdot 2^{-1} + 1 \cdot 2^{-2} + 0 \cdot 2^{-3}+ 1 \cdot 2^{-4}+ 1 \cdot 2^{-5} + 1 \cdot 2^{-6} = 0.359375\hspace{0.05cm}. $$ | ||
| + | *Proposition 1: $r_1 = (0.101100)_{\text{binary}}$ must be ruled out because the associated decimal value is $r_1 > (0.5)_{\text{decimal}}$ . | ||
| + | *The last suggested solution is also wrong, since $r_3 = (0.001011)_{\text{binary}} < (0.01)_{\text{binary}} = (0.25)_{\text{decimal}}$. | ||
| + | |||
| − | |||
| − | |||
{{ML-Fuß}} | {{ML-Fuß}} | ||
| − | [[Category: | + | [[Category:Information Theory: Exercises|^2.4 Further Source Coding Methods^]] |
Latest revision as of 16:14, 30 August 2021
Arithmetic coding is a special form of entropy coding: The symbol probabilities must also be known here.
In this exercise, we assume $M = 3$ symbols, which we name with $\rm X$, $\rm Y$ and $\rm Z$. While Huffman coding is done symbol by symbol, in Arithmetic Coding $(\rm AC)$ a sequence of symbols of length $N$ is encoded together. The coding result is a real numerical value $r$ from the interval
- $$I = \big[B, \ E \big) = \big[B, \ B +{\it \Delta} \big)\hspace{0.05cm}.$$
This notation means:
- The beginning $B$ belongs to the interval $I$.
- The end $E$ is no longer contained in $I$ .
- The interval width is ${\it} {\it \Delta} = E - B$.
Of the infinite number of possible values $r \in I$ $($since $r$ is real-valued, i.e. not an integer$)$, the numerical value that gets by with the smallest number of bits is selected. Here are two examples for clarification:
- The decimal value $r = 3/4$ can be represented with two bits:
- $$r = 1 \cdot 2^{-1} + 1 \cdot 2^{-2} = 0.75 \hspace{0.3cm} \Rightarrow\hspace{0.3cm}\text{binary:}\hspace{0.25cm} 0.11\hspace{0.3cm}\Rightarrow\hspace{0.3cm}\text {Code:} \hspace{0.25cm} \boldsymbol{\rm 11} \hspace{0.05cm}, $$
- The decimal value $r = 1/3$ , on the other hand, requires an infinite number of bits:
- $$r = 0 \cdot 2^{-1} + 1 \cdot 2^{-2} + 1 \cdot 2^{-3}+ 1 \cdot 2^{-4}+ 0 \cdot 2^{-5} + 1 \cdot 2^{-6} + \hspace{0.05cm}\text{...}$$
- $$ \Rightarrow\hspace{0.3cm}\text{binär:} \hspace{0.25cm}0.011101\hspace{0.05cm}\text{...}\hspace{0.3cm}\Rightarrow\hspace{0.3cm} \text{Code:} \hspace{0.25cm} \boldsymbol{\rm 011101}\hspace{0.05cm}\text{...} \hspace{0.05cm}. $$
In this task we restrict ourselves to the determination of the current interval $I$, marked by the beginning $B$ as well as the end $E$ and the width ${\it \Delta}$ respectively.
- This determination is done according to the interval nesting in the above diagram.
- The hatching shows that the sequence begins with the ternary symbols $\rm XXY$ .
The algorithm works as follows:
- Before the beginning (quasi at the zero symbol) the entire probability range is divided into three areas according to the probabilities $p_{\rm X}$, $p_{\rm Y}$ and $p_{\rm Z}$ . The limits are
- $$B_0 = 0\hspace{0.05cm},\hspace{0.4cm}C_0 = p_{\rm X}\hspace{0.05cm},\hspace{0.4cm}D_0 = p_{\rm X} + p_{\rm Y}\hspace{0.05cm},\hspace{0.4cm} E_0 = p_{\rm X} + p_{\rm Y}+ p_{\rm Z} = 1\hspace{0.05cm}.$$
- The first symbol of the sequence to be coded is $\rm X$. This means: The selected interval is limited by $B_0$ and $C_0$ .
- This interval is divided with new beginning $B_1 = B_0$ and new end $E_1 = C_0$ in the same way as the total range in the zero step.
The intermediate values are $C_1$ and $D_1$. - The further interval division is your task. For example, in subtask (2) the boundaries $B_2$, $C_2$, $D_2$ and $E_2$ for the second symbol $\rm X$ are to be determined
and in subtask (3) the boundaries $B_3$, $C_3$, $D_3$ and $E_3$ for the third symbol $\rm Y$ are to be determined.
Hints:
- The exercise belongs to the chapter Further source coding methods.
- In particular, reference is made to the page Arithmetic Coding.
- The binary representation of the selected interval is dealt with in Exercise 2.11Z.
Questions
Solution
(1) From the graph on the information page you can read the probabilities:
- $$p_{\rm X} = 0.7\hspace{0.05cm},\hspace{0.2cm}p_{\rm Y} = 0.1\hspace{0.05cm},\hspace{0.2cm}p_{\rm Z} = 0.2\hspace{0.05cm}.$$
(2) The second symbol is also $\rm X$. Using the same procedure as in the task description, we get
- $$B_2 \hspace{0.1cm}\underline{= 0}\hspace{0.05cm},\hspace{0.2cm}C_2 = 0.49 \cdot 0.7 \hspace{0.1cm}\underline{= 0.343}\hspace{0.05cm},\hspace{0.2cm} D_2 \hspace{0.1cm} \underline{= 0.392}\hspace{0.05cm},\hspace{0.2cm}E_2 = C_1 \hspace{0.1cm}\underline{= 0.49} \hspace{0.05cm}.$$
(3) For the third symbol $\rm Y$ the limitations $B_3 = C_2$ and $E_3 = D_2$ now apply:
- $$B_3 \hspace{0.1cm}\underline{= 0.343}\hspace{0.05cm},\hspace{0.2cm}C_3 \hspace{0.1cm}\underline{= 0.3773}\hspace{0.05cm},\hspace{0.2cm} D_3 \hspace{0.1cm} \underline{= 0.3822}\hspace{0.05cm},\hspace{0.2cm}E_3 \hspace{0.1cm}\underline{= 0.392} \hspace{0.05cm}.$$
(4) Solution suggestion 1 is correct:
- From $B_4 = 0.343 = B_3$ (to be read in the diagram on the data sheet) it follows that the fourth source symbol was an $\rm X$.
(5) Proposed solutions 2 and 3 are correct:
- The graph shows the interval nesting with all previous results. You can see from the hatching that the second suggested solution gives the correct sequence of symbols: $\rm XXYXXXZ$.
- The interval width $\it \Delta$ can really be determined according to suggestion 3. It holds:
- $${\it \Delta} = 0.359807 - 0.3564456 = 0.003614 \hspace{0.05cm},$$
- $$\Rightarrow \hspace{0.3cm} {\it \Delta} =p_{\rm X}^5 \cdot p_{\rm Y} \cdot p_{\rm Z} = 0.7^5 \cdot 0.1 \cdot 0.2 = 0.003614 \hspace{0.05cm}. $$
(6) Correct is the proposed solution 2 ⇒ $r_2 = (0.010111)_{\text{binary}}$, because of:
- $$r_2 = 0 \cdot 2^{-1} + 1 \cdot 2^{-2} + 0 \cdot 2^{-3}+ 1 \cdot 2^{-4}+ 1 \cdot 2^{-5} + 1 \cdot 2^{-6} = 0.359375\hspace{0.05cm}. $$
- Proposition 1: $r_1 = (0.101100)_{\text{binary}}$ must be ruled out because the associated decimal value is $r_1 > (0.5)_{\text{decimal}}$ .
- The last suggested solution is also wrong, since $r_3 = (0.001011)_{\text{binary}} < (0.01)_{\text{binary}} = (0.25)_{\text{decimal}}$.