Aufgaben:Exercise 2.6: Two-Way Channel

• Return to book

Impulse response of the two-way channel

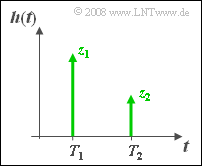
The so-called two-way channel is characterised by the following impulse response  $($with  $T_1 < T_2)$:

$$h(t) = z_1 \cdot \delta ( t - T_1) + z_2 \cdot \delta ( t - T_2).$$

• Except for a few combinations of the system parameters  $z_1$,  $T_1$,  $z_2$  and  $T_2$,  this channel will result in linear distortions.
• There is a distortion-free channel at hand only if not a single input signal is distorted by it. This means:   Even if the channel is distorting, there may be special cases where indeed  $y(t) = \alpha \cdot x(t - \tau)$  applies.

The test signals applied to the system input are:

• a  Dirac comb  $x_1(t)$  at a time interval of  $T_0 = 1 \ \rm ms$ whose spectral function  $X_1(f)$  is also a Dirac comb with an interval of  $f_0 = 1/T_0 = 1 \ \rm kHz$:

$$x_1(t) = \sum_{n = - \infty}^{+\infty} \delta ( t - n \cdot T_0) ,\hspace{0.5cm} X_1(f) = T_0 \cdot \sum_{k = - \infty}^{+\infty} \delta ( f - k \cdot f_0) ,$$

• a cosine signal with frequency  $f_2 = 250 \ \rm Hz$:

$$x_2(t) = \cos(2 \pi \cdot f_2 \cdot t) ,$$

• the sum of two cosine signals with frequencies  $f_2 = 250 \ \rm Hz$  and  $f_3 = 1250 \ \rm Hz$:

$$x_3(t) = \cos(2 \pi \cdot f_2 \cdot t) + \cos(2 \pi \cdot f_3 \cdot t) .$$

Please note:

• The task belongs to the chapter   Linear Distortions.

• To spare you calculations the result for the parameter set  $\big [z_1 = 1$,  $T_1 = 0$,  $z_2 =0.5$,  $T_2 = 1 \ \rm ms\big ]$  is given:

$$|H(f = f_2)| = |H(f = f_3)| = \sqrt{1.25} \approx 1.118, \; \; \; \; b(f = f_2) = b(f = f_3) = \arctan (0.5) \approx 0.464.$$

Questions

1

Which of the following statements are true?

	The parameter set  $\big[z_1 = 1$, $T_1 = 0$, $z_2 =0 \big]$  is the only possible one to describe the ideal channel.
	Any distortion-free channel is captured by the two combinations  $\big[z_1 \ne 0, \; z_2 = 0 \big]$  or  $\big[z_1 = 0, \; z_2 \ne 0 \big]$ .
	The values  $\big[z_1 \ne 0\big]$  and  $\big[z_2 \ne 0\big]$  result in a distortion-free channel if  $T_1$  and  $T_2$  are optimally adjusted.

2

The following holds: $\big[z_1 = 1$,  $T_1 = 0$,  $z_2 =0.5$,  $T_2 = 1 \ \rm ms\big ]$.  Compute the frequency response  $H(f)$  of this channel.
What are the values at multiples of  $1 \ \rm kHz$?

${\rm Re}\big[H(f = n \cdot 1 \ {\rm kHz})\big] \ = \ $

${\rm Im}\big[H(f = n \cdot 1 \ {\rm kHz})\big] \ = \ $

3

The Dirac comb $x_1(t)$  is applied to the input of the system with the same parameters as in subtask  (2) .
Which statements are true for the output signal $y_1(t)$ ?

	$y_1(t)$  is attenuated/amplified by a constant compared to $x_1(t)$ .
	$y_1(t)$  is shifted with respect to $x_1(t)$ .
	$y_1(t)$  exhibits distortions with respect to $x_1(t)$ .

4

Compute the signal $y_2(t)$  as the system response to the cosine signal $x_2(t)$.   What is the signal value at time $t = 0$ ?

$y_2(t = 0) \ = \ $

5

Which statements are true regarding the signals $x_3(t)$  and  $y_3(t)$ ?

	$y_3(t)$  does not exhibit any distortions with respect to $x_3(t)$ .
	$y_3(t)$  exhibits attenuation distortions with respect to $x_3(t)$ .
	$y_3(t)$  exhibits phase distortions with respect to $x_3(t)$ .

Solution

Solution

(1)  Statements 1 and 2 are correct:

• $h(t) = \delta(t)$  is true with $z_1 = 1$, $T_1 = 0$ and $z_2 =0$  and correspondingly $H(f) = 1$ so that $y(t) = x(t)$  will always hold.
• Each distortion-free channel impulse response $h(t)$  consists of a single Dirac function, for example at $t = T_1$.
• This case is accounted for in the model by $z_2 =0$ . Thus, the frequency response is:

$$H(f)= z_1\cdot {\rm e}^{-{\rm j}\cdot \hspace{0.05cm}2 \pi f T_1} \ \Rightarrow \ y(t) = z_1 \cdot x(t- T_1).$$

• In contrast, the channel will lead to linear distortions whenever $z_1$  and $z_2$  are simultaneously non-zero.

(2)  The Fourier transformation of the impulse response $h(t)$  results in the equation:

$$H(f) = z_1\cdot {\rm e}^{-{\rm j}\hspace{0.05cm} \cdot \hspace{0.05cm}2 \pi f T_1}+ z_2\cdot {\rm e}^{-{\rm j}\hspace{0.05cm} \cdot \hspace{0.05cm}2 \pi f T_2} .$$

• The following is obtained with $z_1 = 1$, $T_1 = 0$, $z_2 =0.5$  and $T_2 = 1 \ \rm ms$ :

$$H(f) =1 + 0.5 \cdot {\rm e}^{-{\rm j}\hspace{0.05cm} \cdot \hspace{0.05cm}2 \pi f T_2}.$$

• Broken down by real and imaginary part, this yields:

$${\rm Re}\big[H(f)\big] = 1 + 0.5 \cdot \cos(2 \pi f \cdot 1\,{\rm ms}) \ \Rightarrow \ \underline{{\rm Re}[H(f = f_1 =1 \ \rm kHz)] = 1.5}, $$

$${\rm Im}\big[H(f)\big] = -0.5 \cdot \sin(2 \pi f \cdot 1\,{\rm ms}) \ \Rightarrow \ \underline{{\rm Im}\big[H(f = f_1 =1 \ \rm kHz)\big] = 0}, $$

(3)  The first answer is the only correct one:

• From  (2)  it follows that the absolute value function is $|H(f)| = 1.5$  and the phase function  $b(f) \equiv 0$ for all multiples of $f_1 =1 \ \rm kHz$ .
• Thus, the phase delay time is also zero in each case for these discrete frequency values.
• But since the spectrum $X_1(f)$  of the Dirac comb has spectral lines exactly at these frequencies,  $y_1(t) = 1.5 \cdot x_1(t)$ holds.

(4)  The absolute value function is:

$$|H(f)| = \sqrt{{\rm Re}[H(f)]^2 + {\rm Im}[H(f)]^2} $$

$$\Rightarrow \; |H(f)| = \sqrt{1 + 0.25 \cdot \cos^2(2 \pi f \cdot T_2)+ \cos(2 \pi f \cdot T_2) + 0.25 \cdot \sin^2(2 \pi f \cdot T_2)} = \sqrt{1.25 + \cos(2 \pi f \cdot T_2) }.$$

• Thus, the following is obtained for the frequency $f_2 =0.25 \ \rm kHz$ :

$$|H(f)| = \sqrt{1.25 + \cos(\frac{\pi}{2} ) }= \sqrt{1.25} = 1.118.$$

• The phase function is generally or at the frequency  $f_2 =0.25 \ \rm kHz$:

$$b(f) = - {\rm arctan}\hspace{0.1cm}\frac{{\rm Im}[H(f)]}{{\rm Re}[H(f)]} = - {\rm arctan}\hspace{0.1cm}\frac{-0.5 \cdot \sin(2 \pi f T_2)}{1+0.5 \cdot \cos(2 \pi f T_2)},$$

$$b(f = f_2) = - {\rm arctan}\hspace{0.1cm}\frac{-0.5 \cdot \sin( \pi/2)}{1+0.5 \cdot \cos(\pi/2)}={\rm arctan}\hspace{0.1cm}\frac{0.5}{1} = 0.464.$$

• Thus, the phase delay time for this frequency is:

$$\tau_2 = \frac {b(f_2)}{2 \pi f_2} = \frac {0.464}{2 \pi \cdot 0.25\,{\rm kHz}} \approx 0.3\,{\rm ms},$$

• Hence, the following holds for the output signal:

$$y_2(t) = 1.118 \cdot \cos(2 \pi \cdot 0.25\,{\rm kHz}\cdot (t - 0.3\,{\rm ms})).$$

• The signal value at zero-time is therefore:

$$y_2(t=0) = 1.118 \cdot \cos(-2 \pi \cdot 0.25\,{\rm kHz} \cdot 0.3\,{\rm ms}) \approx 1.118 \cdot 0.891 \hspace{0.15cm}\underline{= 0.996}.$$

(5)  Both frequencies have the same attenuation factor $\alpha = 1.118$ . Therefore, no attenuation distortions are observed.

• The following is obtained for the phase function with $f_3 = 1.25 \ \rm kHz$  and  $T_2 = 1 \ \rm ms$ :

$$b(f = f_3) = - {\rm arctan}\hspace{0.1cm}\frac{-0.5 \cdot \sin( 2.5 \pi)}{1+0.5 \cdot \cos(2.5 \pi)}= 0.464 = b(f = f_2),$$

so exactly the same value as for the frequency $f_2 = 0.25 \ \rm kHz$.

• Despite this, however, phase distortions now occur since for $f_3$  the phase delay time is only $\tau = 60 \ µ \rm s$  anymore.

• So, the following can be formulated for the output signal:

$$y_3(t) = 1.118 \cdot \cos(2 \pi f_2 \cdot (t - 0.3\,{\rm ms}) + 1.118 \cdot \cos(2 \pi f_3 \cdot (t - 0.06\,{\rm ms})$$

$$\Rightarrow \; \; y_3(t) = 1.118 \cdot \cos(2 \pi f_2 \cdot t - 27^\circ) + 1.118 \cdot \cos(2 \pi f_3 \cdot t - 27^\circ).$$

Accordingly, the correct answer is 3:

• So, there are phase distortions although for both oscillations, $\varphi_2 = \varphi_3= 27^\circ$  holds.
• To avoid phase distortions
  • the phase delay times $\tau_2$ and $\tau_3$ would have to be equal and
  • the phase values $\varphi_2$  and  $\varphi_3$  would have to increase linearly with the corresponding frequencies.