Difference between revisions of "Aufgaben:Exercise 5.3Z: Zero-Padding"
m (Text replacement - "analyse" to "analyze") |
|||
| (20 intermediate revisions by 5 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Signal_Representation/Possible_Errors_When_Using_DFT |
}} | }} | ||
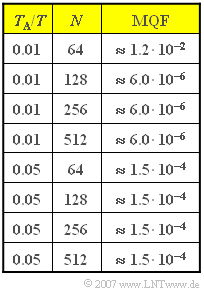
| − | [[File:P_ID1146__Sig_Z_5_3_neu.png|right|frame|MQF& | + | [[File:P_ID1146__Sig_Z_5_3_neu.png|right|frame|$\rm MQF$ values as a function <br>of $T_{\rm A} /T$ and $N$]] |
| − | + | We consider the DFT of a rectangular pulse $x(t)$ of height $A =1$ and duration $T$. Thus the spectral function $X(f)$ has a $\sin(f)/f$–shaped course. | |
| − | + | For this special case the influence of the DFT parameter $N$ is to be analyzed, whereby the interpolation point distance in the time domain should always be $T_{\rm A} = 0.01T$ or $T_{\rm A} = 0.05T$. | |
| + | |||
| + | The resulting values for the "mean square error" $\rm (MSE)$ of the grid values in the frequency domain are given opposite for different values of $N$. Here, we use instead of $\rm MSE$ the designation $\rm MQF$ ⇒ (German: "Mittlerer Quadratischer Fehler"): | ||
| − | |||
:$${\rm MQF} = \frac{1}{N}\cdot \sum_{\mu = 0 }^{N-1} | :$${\rm MQF} = \frac{1}{N}\cdot \sum_{\mu = 0 }^{N-1} | ||
\left|X(\mu \cdot f_{\rm A})-\frac{D(\mu)}{f_{\rm A}}\right|^2 \hspace{0.05cm}.$$ | \left|X(\mu \cdot f_{\rm A})-\frac{D(\mu)}{f_{\rm A}}\right|^2 \hspace{0.05cm}.$$ | ||
| − | + | Thus, for $T_{\rm A}/T = 0.01$ , $101$ of the DFT coefficients $d(ν)$ are always different from zero. | |
| + | |||
| + | :* Of these, $99$ have the value $1$ and the two marginal coefficients are each equal to $0.5$. | ||
| + | |||
| + | :* If $N$ is increased, the DFT coefficient field is filled with zeros. | ||
| + | |||
| + | :*This is then referred to as $\text{zero padding}$. | ||
| − | |||
| − | |||
| − | |||
| + | ''Hints:'' | ||
| + | *This task belongs to the chapter [[Signal_Representation/Possible_Errors_When_Using_DFT|Possible errors when using DFT]]. | ||
| + | |||
| + | *The theory for this chapter is summarised in the (German language) learning video <br> [[Fehlermöglichkeiten_bei_Anwendung_der_DFT_(Lernvideo)|Fehlermöglichkeiten bei Anwendung der DFT]] ⇒ "Possible errors when using DFT". | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Which statements can be derived from the given MQF values $($valid for $T_{\rm A}/T = 0.01$ and $N ≥ 128)$? |
|type="[]"} | |type="[]"} | ||
| − | + | + | + The $\rm MQF$ value here is almost independent of $N$. |
| − | - | + | - The $\rm MQF$ value is determined by the truncation error. |
| − | + | + | + The $\rm MQF$ value is determined by the aliasing error. |
| − | { | + | {Let $T_{\rm A}/T = 0.01$. What is the distance $f_{\rm A}$ of adjacent samples in the frequency domain for $N = 128$ and $N = 512$? |
|type="{}"} | |type="{}"} | ||
| − | $N = 128$: $f_{\rm A} \cdot T $ | + | $N = 128$: $f_{\rm A} \cdot T \ = \ $ { 0.781 3% } |
| − | $N = 512$: $f_{\rm A} \cdot T $ | + | $N = 512$: $f_{\rm A} \cdot T \ = \ $ { 0.196 3% } |
| − | { | + | {What does the product $\text{MQF} \cdot f_{\rm A}$ indicate in terms of DFT quality? |
|type="[]"} | |type="[]"} | ||
| − | + | + | + The product $\text{MQF} \cdot f_{\rm A}$ considers the accuracy and density of the DFT values. |
| − | - | + | - The product $\text{MQF} \cdot f_{\rm A}$ should be as large as possible. |
| − | + | { $N = 128$ is now fixed. Which statements apply to the comparison of the DFT results with $T_{\rm A}/T = 0.01$ und $T_{\rm A}/T = 0.05$ ? | |
| − | { | ||
|type="[]"} | |type="[]"} | ||
| − | + | + | + With $T_{\rm A}/T = 0.05$ you get a finer frequency resolution. |
| − | - | + | - With $T_{\rm A}/T = 0.05$ the $\rm MQF$ value is smaller. |
| − | - | + | - With $T_{\rm A}/T = 0.05$ the influence of the truncation error decreases. |
| − | + | + | + With $T_{\rm A}/T = 0.05$ the influence of the aliasing error increases. |
| − | { | + | {Now $N = 64$. Which statements are true for the comparison of the DFT results with $T_{\rm A}/T = 0.01$ und $T_{\rm A}/T = 0.05$ ? |
|type="[]"} | |type="[]"} | ||
| − | + | + | + With $T_{\rm A}/T = 0.05$ you get a finer frequency resolution. |
| − | + | + | + With $T_{\rm A}/T = 0.05$ the $\rm MQF$ value is smaller. |
| − | + | + | + With $T_{\rm A}/T = 0.05$ the influence of the truncation error decreases. |
| − | + | + | + With $T_{\rm A}/T = 0.05$ the influence of the aliasing error increases. |
| Line 72: | Line 75: | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''1 | + | '''(1)''' <u>Proposed solutions 1 and 3</u> are correct: |
| + | *Already with $N = 128$, $T_{\rm P} = 1.28 \cdot T$, i.e. larger than the width of the rectangle. | ||
| + | *Thus the truncation error plays no role at all here. | ||
| + | *The $\rm MQF$ value is determined solely by the aliasing error. | ||
| + | *The numerical values clearly confirm that $\rm MQF$ is (almost) independent of $N$. | ||
| + | |||
| + | |||
| + | |||
| + | '''(2)''' From $T_{\rm A}/T = 0.01$ follows $f_{\rm P} \cdot T = 100$. | ||
| + | *The supporting values of $X(f)$ thus lie in the range $–50 ≤ f \cdot T < +50$. | ||
| + | *For the distance between two samples in the frequency range, $f_{\rm A} = f_{\rm P}/N$ applies. This gives the following results: | ||
| + | :*$N = 128$: $f_{\rm A} \cdot T \; \underline{\approx 0.780}$, | ||
| + | :*$N = 512$: $f_{\rm A} \cdot T \; \underline{\approx 0.195}$. | ||
| + | |||
| + | |||
| + | |||
| + | '''(3)''' The <u>first statement</u> is correct: | ||
| + | *For $N = 128$ , the product is $\text{MQF} \cdot f_{\rm A} \approx 4.7 \cdot 10^{-6}/T$. For $N = 512$ , the product is smaller by a factor of about $4$ . | ||
| + | *This means that „zero padding” does not achieve greater DFT accuracy, but a finer "resolution" of the frequency range. | ||
| + | *The product $\text{MQF} \cdot f_{\rm A}$ takes this fact into account; it should always be as small as possible. | ||
| − | |||
| − | |||
| − | |||
| − | ''' | + | '''(4)''' <u>Proposed solutions 1 and 4</u> are correct: |
| − | * | + | *Because of $T_{\rm A} \cdot f_{\rm A} \cdot N = 1$ , a constant $N$ always results in a smaller $f_{\rm A}$ value when $T_{\rm A}$ is increased. |
| − | + | *From the table on the information page, one can see that the mean square error $\rm (MQF)$ is significantly increased $($by a factor of about $400)$. | |
| + | *The effect is due to the aliasing error, since the transition from $T_{\rm A}/T = 0.01$ auf $T_{\rm A}/T = 0.05$ reduces the frequency period by a factor of $5$ . | ||
| + | *The truncation error, on the other hand, continues to play no role with the rectangular pulse as long as $T_{\rm P} = N \cdot T_{\rm A}$ is greater than the pulse duration $T$. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | '''5 | + | '''(5)''' <u>All statements are true</u>: |
| − | * | + | *With the parameter values $N = 64$ and $T_{\rm A}/T = 0.01$ , an extremely large truncation error occurs. |
| − | * | + | *All time coefficients are $1$, so the DFT incorrectly interprets a DC signal instead of the rectangular function. |
{{ML-Fuß}} | {{ML-Fuß}} | ||
__NOEDITSECTION__ | __NOEDITSECTION__ | ||
| − | [[Category: | + | [[Category:Signal Representation: Exercises|^5.3 Possible DFT Errors^]] |
Latest revision as of 12:47, 22 September 2021
We consider the DFT of a rectangular pulse $x(t)$ of height $A =1$ and duration $T$. Thus the spectral function $X(f)$ has a $\sin(f)/f$–shaped course.
For this special case the influence of the DFT parameter $N$ is to be analyzed, whereby the interpolation point distance in the time domain should always be $T_{\rm A} = 0.01T$ or $T_{\rm A} = 0.05T$.
The resulting values for the "mean square error" $\rm (MSE)$ of the grid values in the frequency domain are given opposite for different values of $N$. Here, we use instead of $\rm MSE$ the designation $\rm MQF$ ⇒ (German: "Mittlerer Quadratischer Fehler"):
- $${\rm MQF} = \frac{1}{N}\cdot \sum_{\mu = 0 }^{N-1} \left|X(\mu \cdot f_{\rm A})-\frac{D(\mu)}{f_{\rm A}}\right|^2 \hspace{0.05cm}.$$
Thus, for $T_{\rm A}/T = 0.01$ , $101$ of the DFT coefficients $d(ν)$ are always different from zero.
- Of these, $99$ have the value $1$ and the two marginal coefficients are each equal to $0.5$.
- If $N$ is increased, the DFT coefficient field is filled with zeros.
- This is then referred to as $\text{zero padding}$.
Hints:
- This task belongs to the chapter Possible errors when using DFT.
- The theory for this chapter is summarised in the (German language) learning video
Fehlermöglichkeiten bei Anwendung der DFT ⇒ "Possible errors when using DFT".
Questions
Solution
- Already with $N = 128$, $T_{\rm P} = 1.28 \cdot T$, i.e. larger than the width of the rectangle.
- Thus the truncation error plays no role at all here.
- The $\rm MQF$ value is determined solely by the aliasing error.
- The numerical values clearly confirm that $\rm MQF$ is (almost) independent of $N$.
(2) From $T_{\rm A}/T = 0.01$ follows $f_{\rm P} \cdot T = 100$.
- The supporting values of $X(f)$ thus lie in the range $–50 ≤ f \cdot T < +50$.
- For the distance between two samples in the frequency range, $f_{\rm A} = f_{\rm P}/N$ applies. This gives the following results:
- $N = 128$: $f_{\rm A} \cdot T \; \underline{\approx 0.780}$,
- $N = 512$: $f_{\rm A} \cdot T \; \underline{\approx 0.195}$.
(3) The first statement is correct:
- For $N = 128$ , the product is $\text{MQF} \cdot f_{\rm A} \approx 4.7 \cdot 10^{-6}/T$. For $N = 512$ , the product is smaller by a factor of about $4$ .
- This means that „zero padding” does not achieve greater DFT accuracy, but a finer "resolution" of the frequency range.
- The product $\text{MQF} \cdot f_{\rm A}$ takes this fact into account; it should always be as small as possible.
(4) Proposed solutions 1 and 4 are correct:
- Because of $T_{\rm A} \cdot f_{\rm A} \cdot N = 1$ , a constant $N$ always results in a smaller $f_{\rm A}$ value when $T_{\rm A}$ is increased.
- From the table on the information page, one can see that the mean square error $\rm (MQF)$ is significantly increased $($by a factor of about $400)$.
- The effect is due to the aliasing error, since the transition from $T_{\rm A}/T = 0.01$ auf $T_{\rm A}/T = 0.05$ reduces the frequency period by a factor of $5$ .
- The truncation error, on the other hand, continues to play no role with the rectangular pulse as long as $T_{\rm P} = N \cdot T_{\rm A}$ is greater than the pulse duration $T$.
(5) All statements are true:
- With the parameter values $N = 64$ and $T_{\rm A}/T = 0.01$ , an extremely large truncation error occurs.
- All time coefficients are $1$, so the DFT incorrectly interprets a DC signal instead of the rectangular function.