Aufgaben:Exercise 3.14: Channel Coding Theorem

• Return to book

Information-theoretical quantities of the  $\rm BSC$   and  $\rm EUC models$

Shannon's  channel coding theorem states that an error-free transmission can be made over a discrete memoryless channel (DMC) with the code rate  $R$  as long as  $R$  is not greater than the channel capacity

$$C = \max_{P_X(X)} \hspace{0.15cm} I(X;Y) \hspace{0.05cm}.$$

The channel coding theorem is to be evaluated numerically in this task, whereby two typical channel models are to be considered:

• the  $\rm BSC$ model  (Binary Symmetric Channel)  with distortion probability $ε = 0.25$  and channel capacity  $C = 1 - H_{\rm bin}(ε),$
• the  $\rm EUC$ model  (from  Extremely Unsymmetric Channel, this designation originates from us and is not common) according to)  Exercise 3.11Z.

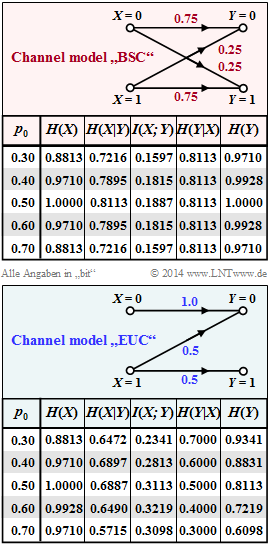
The graphs show the numerical values of the information-theoretical quantities for the two channels  $\rm BSC$  and  $\rm EUC$:

• the source entropy  $H(X),$
• the equivocation  $H(X|Y),$
• the mutual information  $I(X; Y),$
• the irrelevance  $H(Y|X),$  and
• the sink entropy  $H(Y).$

The parameter in these tables is  $p_0 = {\rm Pr}(X = 0)$  in the range between  $p_0 = 0.3$  to  $p_0 = 0.7$. 
For the second source symbol probability,   $p_1 = {\rm Pr}(X = 1) =1 - p_0$.

Hints:

• The exercise belongs to the chapter  Application to Digital Signal Transmission.
• Reference is made in particular to the page  Definition and meaning of channel capacity.

Questions

1

Which statements are true for uncoded transmission   ⇒  $\underline{R = 1}$ assuming $p_0 = p_1 = 0.5$ ?

	BSC results in a smaller bit error probability.
	EUC results in a smaller bit error probability.
	Both models lead to the same bit error probability.

2

With  $\underline{R = 1}$  can the result be (formally) improved by other values of  $p_0$  or  $p_1 ?

	For both channels.
	With the BSC model.
	With the EUC model.
	Not for any model.

3

Over which channel can error-free transmission be achieved with the  $\underline{R = 0.16}$ ?

	For both channels.
	For the BSC model.
	With the EUC model.
	With none of the models.

4

Over which channel can error-free transmission be achieved with the  $\underline{R = 0.32}$ ?

	Over both channels.
	For the BSC model.
	With the EUC model.
	With no model.

5

Over which channel can error-free transmission be achieved with the rate  $\underline{R = 0.48}$ ?

	For both channels.
	For the BSC model.
	With the EUC model.
	With none of the models.

Solution

Solution

(1)   Proposed solution 3 is correct:

• The BSC error probability is  ⇒   $R = 1$ with $p_0 = p_1 = 0.5$  for uncoded transmission:  

$$p_{\rm B} = 0.5 \cdot 0.25 + 0.5 \cdot 0.25=0.25 \hspace{0.05cm}.$$

• Correspondingly, with the same boundary conditions for the EUC model::

$$p_{\rm B} = 0.5 \cdot 0 + 0.5 \cdot 0.5=0.25 \hspace{0.05cm}.$$

(2)   Proposed solution 3 is correct:

• In the BSC model with the distortion probability  $ε = 0.25$ , for uncoded transmission   ⇒   $R = 1$  , the bit error probability is equal to  $p_{\rm B} = 0.25$. regardless of  $p_0$  and  $p_1$
• In contrast, with the EUC model, for example, a smaller bit error probability is obtained with  $p_0 = 0.6$  and  $p_1 = 0.4$ :

$$p_{\rm B} = 0.6 \cdot 0 + 0.4 \cdot 0.5=0.2 \hspace{0.05cm}.$$

• Note, however, that now the source entropy is no longer  $H(X) = 1\ \rm (bit)$  but only  $H(X) = H_{bin} (0.6) = 0.971 \ \rm (bit)$.
• In the limiting case  $p_0 = 1$ , only zeros are transmitted and  $H(X) = 0$.  For the bit error probability, however, the following then actually applies:

$$p_{\rm B} = 1 \cdot 0 + 0 \cdot 0.5=0 \hspace{0.05cm}.$$

So no information is transmitted, but it is transmitted with the bit error probability "zero".

(3)   Proposed solution 1 is correct:

• From the graph on the information page, it can be read for the capacities of the two channels:

$$C_{\rm BSC} = 0.1887 \ \rm {bit/use}, \hspace{0.5cm}C_{rm EUC} = 0.3219 \ \rm {bit/use}.$$

• According to the channel coding theorem, a channel coding can be found at  $R ≤ C$  with which the error probability can be made zero.
• For both channels this condition is true with rate  $R = 0.16$ .

(4)   Proposed solution 3 is correct:

• With the EUC model, the necessary condition   $R ≤ C$  for an error-free transmission is fulfilled with  $R = 0.32$  and  $C = 0.3219$ 
• However, the prerequisite for this is the probability function   $P_X(X) = (0.6,\ 0.4).$
• In contrast, for equally probable symbols   ⇒   $P_X(X) = (0.5,\ 0.5)$  the mutual information  $I(X; Y) = 0.3113$ would result,
  i.e. a smaller value than for the channel capacity  $C$, and  $I(X; Y) < R$ also applies.
• It can be seen that the EUC model offers more potential for the application of channel coding than the BSC model.  Here, for example, it can be exploited in the code that a transmitted "0" is always transmitted without errors.

(5)   The comments on subtasks  (3)  and  (4)  show that theproposed solution 4 applies.