Difference between revisions of "Aufgaben:Exercise 4.5: Mutual Information from 2D-PDF"
| Line 36: | Line 36: | ||
Hints: | Hints: | ||
| − | *The exercise belongs to the chapter [[Information_Theory/ | + | *The exercise belongs to the chapter [[Information_Theory/AWGN_Channel_Capacity_for_Continuous_Input#Mutual_information_between_value-continuous_random_variables|AWGN channel capacitance with value-continuous input]]. |
*Let the following differential entropies also be given: | *Let the following differential entropies also be given: | ||
Revision as of 16:47, 1 October 2021
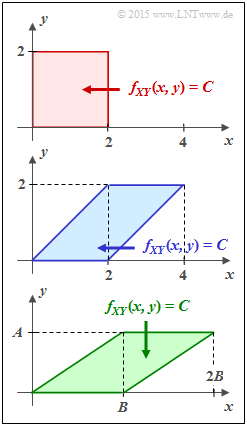
Given here are the three different two-dimensional regions $f_{XY}(x, y)$, which in the task are identified by their fill colors with
- red joint PDF,
- blue joint PDF,
- green joint PDF,
respectively. Within each of the regions shown, let $f_{XY}(x, y) = C = \rm const.$
For example, the mutual information between the value-continuous random variables $X$ and $Y$ can be calculated as follows:
- $$I(X;Y) = h(X) + h(Y) - h(XY)\hspace{0.05cm}.$$
For the differential entropies used here, the following equations apply:
- $$h(X) = -\hspace{-0.7cm} \int\limits_{x \hspace{0.05cm}\in \hspace{0.05cm}{\rm supp}(f_X)} \hspace{-0.55cm} f_X(x) \cdot {\rm log} \hspace{0.1cm} \big[f_X(x)\big] \hspace{0.1cm}{\rm d}x \hspace{0.05cm},$$
- $$h(Y) = -\hspace{-0.7cm} \int\limits_{y \hspace{0.05cm}\in \hspace{0.05cm}{\rm supp}(f_Y)} \hspace{-0.55cm} f_Y(y) \cdot {\rm log} \hspace{0.1cm} \big[f_Y(y)\big] \hspace{0.1cm}{\rm d}y \hspace{0.05cm},$$
- $$h(XY) = \hspace{0.1cm}-\hspace{0.2cm} \int \hspace{-0.9cm} \int\limits_{\hspace{-0.5cm}(x, y) \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp} (f_{XY}\hspace{-0.08cm})} \hspace{-0.6cm} f_{XY}(x, y) \cdot {\rm log} \hspace{0.1cm} \big[ f_{XY}(x, y) \big] \hspace{0.15cm}{\rm d}x\hspace{0.15cm}{\rm d}y\hspace{0.05cm}.$$
- For the two marginal probability density functions, the following holds:
- $$f_X(x) = \hspace{-0.5cm} \int\limits_{\hspace{-0.2cm}y \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp} (f_{Y}\hspace{-0.08cm})} \hspace{-0.4cm} f_{XY}(x, y) \hspace{0.15cm}{\rm d}y\hspace{0.05cm},$$
- $$f_Y(y) = \hspace{-0.5cm} \int\limits_{\hspace{-0.2cm}x \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp} (f_{X}\hspace{-0.08cm})} \hspace{-0.4cm} f_{XY}(x, y) \hspace{0.15cm}{\rm d}x\hspace{0.05cm}.$$
Hints:
- The exercise belongs to the chapter AWGN channel capacitance with value-continuous input.
- Let the following differential entropies also be given:
- If $X$ is triangularly distributed between $x_{\rm min}$ and $x_{\rm max}$, then:
- $$h(X) = {\rm log} \hspace{0.1cm} [\hspace{0.05cm}\sqrt{ e} \cdot (x_{\rm max} - x_{\rm min})/2\hspace{0.05cm}]\hspace{0.05cm}.$$
- If $Y$ is equally distributed between $y_{\rm min}$ and $y_{\rm max}$, then holds:
- $$h(Y) = {\rm log} \hspace{0.1cm} \big [\hspace{0.05cm}y_{\rm max} - y_{\rm min}\hspace{0.05cm}\big ]\hspace{0.05cm}.$$
- All results should be expressed in "bit". This is achieved with $\log$ ⇒ $\log_2$.
Questions
Solution
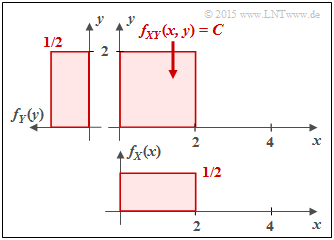
(1) For the rectangular joint PDF $f_{XY}(x, y)$ there are no statistical ties between $X$ and $Y$ ⇒ $\underline{I(X;Y) = 0}$.
Formally, this result can be proved with the following equation:
- $$I(X;Y) = h(X) \hspace{-0.05cm}+\hspace{-0.05cm} h(Y) \hspace{-0.05cm}- \hspace{-0.05cm}h(XY)\hspace{0.02cm}.$$
- The red area 2D-WDF $f_{XY}(x, y)$ is $F = 4$. Since $f_{XY}(x, y)$ is constant in this area and the volume under $f_{XY}(x, y)$ must be equal to $1$ , the height is $C = 1/F = 1/4$.
- From this follows for the differential joint entropy in "bit":
- $$h(XY) \ = \ \hspace{0.1cm}-\hspace{0.2cm} \int \hspace{-0.9cm} \int\limits_{\hspace{-0.5cm}(x, y) \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp} \hspace{0.03cm}(\hspace{-0.03cm}f_{XY}\hspace{-0.08cm})} \hspace{-0.6cm} f_{XY}(x, y) \cdot {\rm log}_2 \hspace{0.1cm} [ f_{XY}(x, y) ] \hspace{0.15cm}{\rm d}x\hspace{0.15cm}{\rm d}y$$
- $$\Rightarrow \hspace{0.3cm} h(XY) \ = \ \ {\rm log}_2 \hspace{0.1cm} (4) \cdot \hspace{0.02cm} \int \hspace{-0.9cm} \int\limits_{\hspace{-0.5cm}(x, y) \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp} \hspace{0.03cm}(\hspace{-0.03cm}f_{XY}\hspace{-0.08cm})} \hspace{-0.6cm} f_{XY}(x, y) \hspace{0.15cm}{\rm d}x\hspace{0.15cm}{\rm d}y = 2 \,{\rm bit}\hspace{0.05cm}.$$
- It is considered that the double integral is equal to $1$ . The pseudo-unit "bit" corresponds to the binary logarithm ⇒ "log2".
Furthermore:
- The marginal probability density functions $f_{X}(x)$ and $f_{Y}(y)$ are rectangular ⇒ uniform distribution between $0$ and $2$:
- $$h(X) = h(Y) = {\rm log}_2 \hspace{0.1cm} (2) = 1 \,{\rm bit}\hspace{0.05cm}.$$
- Substituting these results into the above equation, we obtain:
- $$I(X;Y) = h(X) + h(Y) - h(XY) = 1 \,{\rm bit} + 1 \,{\rm bit} - 2 \,{\rm bit} = 0 \,{\rm (bit)} \hspace{0.05cm}.$$
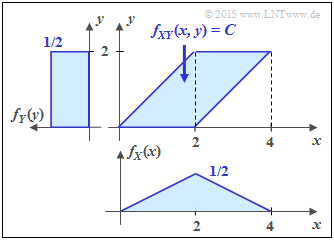
(2) Also for this parallelogram we get $F = 4, \ C = 1/4$ as well as $h(XY) = 2$ bit.
- Here, as in subtask (1) , the random variable $Y$ is uniformly distributed between $0$ and $2$ ⇒ $h(Y) = 1$ bit.
- In contrast, $X$ is triangularly distributed between $0$ and $4$ $($with maximum at $2)$.
- This results in the same differential entropy $h(Y)$ as for a symmetric triangular distribution in the range between $±2$ (see specification sheet):
- $$h(X) = {\rm log}_2 \hspace{0.1cm} \big[\hspace{0.05cm}2 \cdot \sqrt{ e} \hspace{0.05cm}\big ] = 1.721 \,{\rm bit}$$
- $$\Rightarrow \hspace{0.3cm} I(X;Y) = 1.721 \,{\rm bit} + 1 \,{\rm bit} - 2 \,{\rm bit}\hspace{0.05cm}\underline{ = 0.721 \,{\rm (bit)}} \hspace{0.05cm}.$$
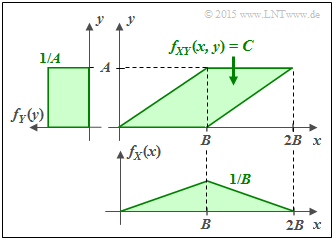
(3) The following properties are obtained for the green conditions:
- $$F = A \cdot B \hspace{0.3cm} \Rightarrow \hspace{0.3cm} C = \frac{1}{A \cdot B} \hspace{0.05cm}\hspace{0.3cm} \Rightarrow \hspace{0.3cm} h(XY) = {\rm log}_2 \hspace{0.1cm} (A \cdot B) \hspace{0.05cm}.$$
- The random variable $Y$ is now uniformly distributed between $0$ and $A$ and the random variable $X$ is triangularly distributed between $0$ and $B$ :
- $$h(X) \ = \ {\rm log}_2 \hspace{0.1cm} (B \cdot \sqrt{ e}) \hspace{0.05cm},$$ $$ h(Y) \ = \ {\rm log}_2 \hspace{0.1cm} (A)\hspace{0.05cm}.$$
- Thus, for the mutual information between $X$ and $Y$:
- $$I(X;Y) \ = {\rm log}_2 \hspace{0.1cm} (B \cdot \sqrt{ {\rm e}}) + {\rm log}_2 \hspace{0.1cm} (A) - {\rm log}_2 \hspace{0.1cm} (A \cdot B)$$
- $$\Rightarrow \hspace{0.3cm} I(X;Y) = \ {\rm log}_2 \hspace{0.1cm} \frac{B \cdot \sqrt{ {\rm e}} \cdot A}{A \cdot B} = {\rm log}_2 \hspace{0.1cm} (\sqrt{ {\rm e}})\hspace{0.15cm}\underline{= 0.721\,{\rm bit}} \hspace{0.05cm}.$$
- $I(X;Y)$ thus independent of WDF parameters $A$ and $B$.
(4) All the above conditions are required.
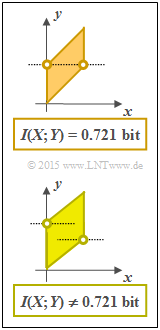
- However, the requirements (2) and (3) are not to be fulfilled for every parallelogram. The adjacent graphic shows two such constellations, where the random variable $X$ is in each case equally distributed between $0$ and $1$ .
- In the upper graph, the plotted points lie at a height ⇒ $f_{Y}(y)$ is triangularly distributed ⇒ $I(X;Y) = 0.721$ bit.
- The lower composite WDF has a different transinformation because the two points are not at the same height
⇒ die WDF $f_{Y}(y)$ has a trapezoidal shape here. - Feeling-wise, I guess $I(X;Y) < 0.721$ bit, since the 2D area more closely approximates a rectangle. If you still feel like it, please check.