Difference between revisions of "Aufgaben:Exercise 4.5Z: Again Mutual Information"
| Line 4: | Line 4: | ||
[[File:P_ID2893__Inf_Z_4_5.png|right|frame|Given joint PDF and <br>graph of differential entropies]] | [[File:P_ID2893__Inf_Z_4_5.png|right|frame|Given joint PDF and <br>graph of differential entropies]] | ||
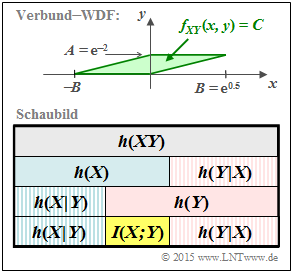
| − | The graph above shows the joint PDF $f_{XY}(x, y)$ to be considered in this task, which is identical to the "green" constellation in [[Aufgaben: | + | The graph above shows the joint PDF $f_{XY}(x, y)$ to be considered in this task, which is identical to the "green" constellation in [[Aufgaben:Exercise_4.5:_Mutual_Information_from_2D-PDF|Exercise 4.5]]. |
* In this sketch $f_{XY}(x, y)$ is enlarged by a factor of $3$ in $y$–direction. | * In this sketch $f_{XY}(x, y)$ is enlarged by a factor of $3$ in $y$–direction. | ||
*In the definition area highlighted in green, the joint PDF is constant equal to $C = 1/F$, where $F$ indicates the area of the parallelogram. | *In the definition area highlighted in green, the joint PDF is constant equal to $C = 1/F$, where $F$ indicates the area of the parallelogram. | ||
Revision as of 12:53, 2 October 2021
The graph above shows the joint PDF $f_{XY}(x, y)$ to be considered in this task, which is identical to the "green" constellation in Exercise 4.5.
- In this sketch $f_{XY}(x, y)$ is enlarged by a factor of $3$ in $y$–direction.
- In the definition area highlighted in green, the joint PDF is constant equal to $C = 1/F$, where $F$ indicates the area of the parallelogram.
In Exercise 4.5 the following differential entropies were calculated:
- $$h(X) \ = \ {\rm log} \hspace{0.1cm} (\hspace{0.05cm}A\hspace{0.05cm})\hspace{0.05cm},$$
- $$h(Y) = {\rm log} \hspace{0.1cm} (\hspace{0.05cm}B \cdot \sqrt{ {\rm e } } \hspace{0.05cm})\hspace{0.05cm},$$
- $$h(XY) = {\rm log} \hspace{0.1cm} (\hspace{0.05cm}F \hspace{0.05cm}) = {\rm log} \hspace{0.1cm} (\hspace{0.05cm}A \cdot B \hspace{0.05cm})\hspace{0.05cm}.$$
In this exercise, the parameter values $A = {\rm e}^{-2}$ and $B = {\rm e}^{0.5}$ are now to be used.
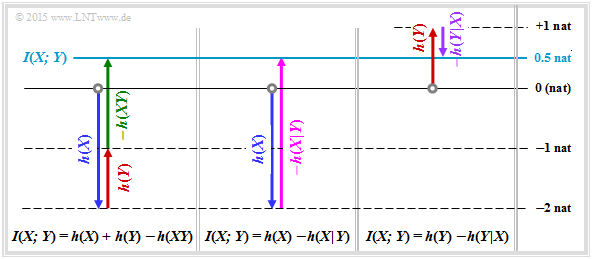
According to the above diagram, the conditional differential entropies $h(Y|X)$ and $h(X|Y)$ should now also be determined and their relation to the mutual information $I(X; Y)$ given.
Hints:
- The exercise belongs to the chapter AWGN channel capacity with value-continuous input.
- If the results are to be given in "nat", this is achieved with "log" ⇒ "ln".
- If the results are to be given in "bit", this is achieved with "log" ⇒ "log2".
Questions
Solution
- The random variable $X$ is uniformly distributed between $0$ and $1/{\rm e}^2={\rm e}^{-2}$:
- $$h(X) = {\rm ln} \hspace{0.1cm} (\hspace{0.05cm}{\rm e}^{-2}\hspace{0.05cm}) \hspace{0.15cm}\underline{= -2\,{\rm nat}}\hspace{0.05cm}. $$
- The random variable $Y$ is triangularly distributed between $±{\rm e}^{-0.5}$:
- $$h(Y) = {\rm ln} \hspace{0.1cm} (\hspace{0.05cm}\sqrt{ {\rm e} } \cdot \sqrt{ {\rm e} } ) = {\rm ln} \hspace{0.1cm} (\hspace{0.05cm}{ { \rm e } } \hspace{0.05cm}) \hspace{0.15cm}\underline{= +1\,{\rm nat}}\hspace{0.05cm}.$$
- The area of the parallelogram is given by
- $$F = A \cdot B = {\rm e}^{-2} \cdot {\rm e}^{0.5} = {\rm e}^{-1.5}\hspace{0.05cm}.$$
- Thus, the 2D WDF in the area highlighted in green has constant height $C = 1/F ={\rm e}^{1.5}$ and we obtain for the joint entropy:
- $$h(XY) = {\rm ln} \hspace{0.1cm} (F) = {\rm ln} \hspace{0.1cm} (\hspace{0.05cm}{\rm e}^{-1.5}\hspace{0.05cm}) \hspace{0.15cm}\underline{= -1.5\,{\rm nat}}\hspace{0.05cm}.$$
- From this we obtain for the mutual information:
- $$I(X;Y) = h(X) + h(Y) - h(XY) = -2 \,{\rm nat} + 1 \,{\rm nat} - (-1.5 \,{\rm nat} ) \hspace{0.15cm}\underline{= 0.5\,{\rm nat}}\hspace{0.05cm}.$$
(2) In general, the relation $\log_2(x) = \ln(x)/\ln(2)$ holds. Thus, using the results of subtask (1), we obtain:
- $$h(X) \ = \ \frac{-2\,{\rm nat}}{0.693\,{\rm nat/bit}}\hspace{0.35cm}\underline{= -2.886\,{\rm bit}}\hspace{0.05cm},$$
- $$h(Y) \ = \ \frac{+1\,{\rm nat}}{0.693\,{\rm nat/bit}}\hspace{0.35cm}\underline{= +1.443\,{\rm bit}}\hspace{0.05cm},$$
- $$h(XY) \ = \ \frac{-1.5\,{\rm nat}}{0.693\,{\rm nat/bit}}\hspace{0.35cm}\underline{= -2.164\,{\rm bit}}\hspace{0.05cm},$$
- $$I(X;Y) \ = \ \frac{0.5\,{\rm nat}}{0.693\,{\rm nat/bit}}\hspace{0.35cm}\underline{= 0.721\,{\rm bit}}\hspace{0.05cm}.$$
- Or also:
- $$I(X;Y) = -2.886 \,{\rm bit} + 1.443 \,{\rm bit}+ 2.164 \,{\rm bit}{= 0.721\,{\rm bit}}\hspace{0.05cm}.$$
(3) The mutual information can also be written in the form $I(X;Y) = h(Y \hspace{-0.05cm}\mid \hspace{-0.05cm} X) - h(Y)$ :
- $$h(Y \hspace{-0.05cm}\mid \hspace{-0.05cm} X) = h(Y) - I(X;Y) = 1 \,{\rm nat} - 0.5 \,{\rm nat} \hspace{0.15cm}\underline{= 0.5\,{\rm nat}= 0.721\,{\rm bit}}\hspace{0.05cm}.$$
(4) For the differential inference entropy, it holds correspondingly:
- $$h(X \hspace{-0.05cm}\mid \hspace{-0.05cm} Y) = h(X) - I(X;Y) = -2 \,{\rm nat} - 0.5 \,{\rm nat} \hspace{0.15cm}\underline{= -2.5\,{\rm nat}= -3.607\,{\rm bit}}\hspace{0.05cm}.$$
- All quantities calculated here are summarized in the graph.
- Arrows pointing up indicate a positive contribution, arrows pointing down indicate a negative contribution.
(5) Correct are the proposed solutions 1 to 3.
Again for clarification:
- For the mutual information $I(X;Y) \ge 0$ always holds.
- In the discrete value case there is no negative entropy, but in the continuous value case there is.