Difference between revisions of "Aufgaben:Exercise 2.5: Distortion and Equalization"
m (Guenter moved page Exercise 2.5: Distortion and Equalisation to Exercise 2.5: Distortion and Equalization) |
|||
| Line 3: | Line 3: | ||
}} | }} | ||
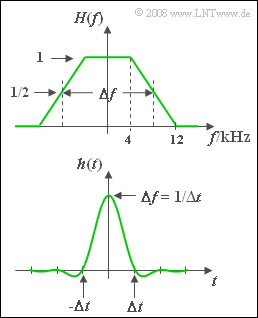
| − | [[File:P_ID907__LZI_A_2_5.png|right|frame|Trapezoidal spectrum (top) | + | [[File:P_ID907__LZI_A_2_5.png|right|frame|Trapezoidal spectrum (top), <br>associated impulse response)]] |
| − | A communication system with input $x(t)$ and output $y(t)$, which is fully described by the trapezoidal frequency response $H(f)$ according to the top graph, is considered. Using the roll-off factor $r = 0.5$ and the equivalent bandwidth $\Delta f = 16 \ \rm kHz$ the corresponding impulse response, which is computable by applying the inverse Fourier transform, is: | + | A communication system with input $x(t)$ and output $y(t)$, which is fully described by the trapezoidal frequency response $H(f)$ according to the top graph, is considered. Using the roll-off factor $r = 0.5$ and the equivalent bandwidth $\Delta f = 16 \ \rm kHz$ the corresponding impulse response, which is computable by applying the inverse Fourier transform, is: |
:$$h(t) = \Delta f \cdot {\rm si}(\pi \cdot \Delta f \cdot t )\cdot | :$$h(t) = \Delta f \cdot {\rm si}(\pi \cdot \Delta f \cdot t )\cdot | ||
{\rm si}(\pi \cdot r \cdot \Delta f \cdot t | {\rm si}(\pi \cdot r \cdot \Delta f \cdot t | ||
| − | ) .$$ | + | ) = \Delta f \cdot {\rm sinc}(\Delta f \cdot t )\cdot |
| − | + | {\rm sinc}(r \cdot \Delta f \cdot t | |
| + | ).$$ | ||
| + | Here the following functions which can be converted into each other are used: | ||
| + | :$${\rm si}(x) = \sin(x)/x,\hspace{0.5cm}{\rm sinc}(x) = \sin(\pi x)/(\pi x).$$ | ||
The available input signals are: | The available input signals are: | ||
*The sum of two harmonic oscillations: | *The sum of two harmonic oscillations: | ||
:$$x_1(t) = {1\, \rm V} \cdot \cos(\omega_1 \cdot t) + {1\, \rm V} \cdot \sin(\omega_2 \cdot | :$$x_1(t) = {1\, \rm V} \cdot \cos(\omega_1 \cdot t) + {1\, \rm V} \cdot \sin(\omega_2 \cdot | ||
t).$$ | t).$$ | ||
| − | :Here, the following holds: $\omega_1 = 2\pi \cdot 2000 \ {\rm 1/s}$ and $\omega_2 \gt \omega_1$. | + | :Here, the following holds: $\omega_1 = 2\pi \cdot 2000 \ {\rm 1/s}$ and $\omega_2 \gt \omega_1$. |
*A periodic triangular signal: | *A periodic triangular signal: | ||
:$$x_2(t) = \frac{8\, \rm V}{\pi^2} \cdot \big[\cos(\omega_0 t) + {1}/{9} \cdot \cos(3\omega_0 t) | :$$x_2(t) = \frac{8\, \rm V}{\pi^2} \cdot \big[\cos(\omega_0 t) + {1}/{9} \cdot \cos(3\omega_0 t) | ||
+ {1}/{25} \cdot \cos(5\omega_0 t) + \hspace{0.05cm}\text{...}\big].$$ | + {1}/{25} \cdot \cos(5\omega_0 t) + \hspace{0.05cm}\text{...}\big].$$ | ||
| − | :It should be noted that the | + | :It should be noted that the basic frequency is $f_0 = 2 \ \rm kHz$ or $3\ \rm kHz$. At time $t = 0$ the signal value in both cases is $1 \ \rm V$. |
*A rectangular pulse $x_3(t)$ with amplitude $A = 1 \ \rm V$ and duration $T = 1 \ \rm ms$. Since its spectrum $X_3(f)$ extends to infinity, $H(f)$ always results in linear distortions here. | *A rectangular pulse $x_3(t)$ with amplitude $A = 1 \ \rm V$ and duration $T = 1 \ \rm ms$. Since its spectrum $X_3(f)$ extends to infinity, $H(f)$ always results in linear distortions here. | ||
Revision as of 15:36, 5 October 2021
A communication system with input $x(t)$ and output $y(t)$, which is fully described by the trapezoidal frequency response $H(f)$ according to the top graph, is considered. Using the roll-off factor $r = 0.5$ and the equivalent bandwidth $\Delta f = 16 \ \rm kHz$ the corresponding impulse response, which is computable by applying the inverse Fourier transform, is:
- $$h(t) = \Delta f \cdot {\rm si}(\pi \cdot \Delta f \cdot t )\cdot {\rm si}(\pi \cdot r \cdot \Delta f \cdot t ) = \Delta f \cdot {\rm sinc}(\Delta f \cdot t )\cdot {\rm sinc}(r \cdot \Delta f \cdot t ).$$
Here the following functions which can be converted into each other are used:
- $${\rm si}(x) = \sin(x)/x,\hspace{0.5cm}{\rm sinc}(x) = \sin(\pi x)/(\pi x).$$
The available input signals are:
- The sum of two harmonic oscillations:
- $$x_1(t) = {1\, \rm V} \cdot \cos(\omega_1 \cdot t) + {1\, \rm V} \cdot \sin(\omega_2 \cdot t).$$
- Here, the following holds: $\omega_1 = 2\pi \cdot 2000 \ {\rm 1/s}$ and $\omega_2 \gt \omega_1$.
- A periodic triangular signal:
- $$x_2(t) = \frac{8\, \rm V}{\pi^2} \cdot \big[\cos(\omega_0 t) + {1}/{9} \cdot \cos(3\omega_0 t) + {1}/{25} \cdot \cos(5\omega_0 t) + \hspace{0.05cm}\text{...}\big].$$
- It should be noted that the basic frequency is $f_0 = 2 \ \rm kHz$ or $3\ \rm kHz$. At time $t = 0$ the signal value in both cases is $1 \ \rm V$.
- A rectangular pulse $x_3(t)$ with amplitude $A = 1 \ \rm V$ and duration $T = 1 \ \rm ms$. Since its spectrum $X_3(f)$ extends to infinity, $H(f)$ always results in linear distortions here.
From subtask (6) onwards, it shall be attempted to eliminate the distortions possibly generated by $H(f)$ by means of a downstream equalizer with
- frequency response $H_{\rm E}(f)$,
- input signal $y(t)$, and
- output signal $z(t)$.
Please note:
- The task belongs to the chapter Linear Distortions.
- In particular, reference is made to the page Entzerrungsverfahren.
- The term "overall distortion" used in the formulation of the questions refers to the input signal $x(t)$ and the output signal $z(t)$.
Questions
Solution
- A linear system is already implicitly assumed by specifying a frequency response so that nonlinear distortions cannot occur.
- Since $H(f)$ is purely real, phase distortions can also be ruled out.
(2) Proposed solutions 1 and 2 are correct:
- The output signal is $y_1(t) = x_1(t)$.
- Thus, the system is not only distortion-free but can also be termed ideal for this application.
(3) Proposed solution 3 is correct:
- In this case, the following is obtained for the output signal:
- $$y_1(t)= 1\,{\rm V}\cdot \cos(2 \pi \cdot f_1 \cdot t) + {1}/{4}\cdot 1\,{\rm V}\cdot \sin(2 \pi \cdot f_2 \cdot t).$$
- While the component at $f_1$ is transmitted unchanged, the sinusoidal component at $f_2$ is attenuated and one-quarter of the original sinusoidal component.
- So, there are attenuation distortions.
(4) The output signal $y_2(t)$ has the following form taking into account the fundamental frequency $f_0 = 3 \ \rm kHz$ :
- $$y_2(t)= \frac{8\,{\rm V}}{\pi^2} \left( \cos(\omega_0 t) + \frac{3}{8}\cdot \frac{1}{9} \cdot \cos(3\omega_0 t)\right) .$$
- The factor $3/8$ describes $H(f = 9 \ \rm kHz)$. All other spectral components at $15 \ \rm kHz$, $21 \ \rm kHz$, etc. are suppressed by the system.
- The strongest deviations between $x_2(t)$ and $y_2(t)$ will occur at the triangle peaks since the missing high frequencies have the strongest effect here. For example, for the time $\underline{t= 0}$ one obtains:
- $$y_2(t=0)= \frac{8\,{\rm V}}{\pi^2} \left( 1 + {3}/{72}\right)= 0.844\,{\rm V} \hspace{0.3cm}\Rightarrow\hspace{0.3cm} \varepsilon_{\rm max} = |y_2(t=0)- x_2(t=0)| \hspace{0.15cm}\underline{= 0.156\,{\rm V}}.$$
(5) With the fundamental frequency $f_0 = 2 \ \rm kHz$ and the transmission values $H(3f_0) = 0.75$, $H(5f_0) = 0.25$, $H(7f_0) = 0$ the following is obtained:
- $$y_2(t=0)= \frac{8\,{\rm V}}{\pi^2} \left( 1 + \frac{3}{4}\cdot \frac{1}{9} + \frac{1}{4} \cdot\frac{1}{25}\right)= 0.886\,{\rm V}\hspace{0.5cm} \Rightarrow \hspace{0.5cm}\varepsilon_{\rm max} \hspace{0.15cm}\underline{= 0.114\,{\rm V}}.$$
(6) In the range up to $4 \ \rm kHz$, $H_{\rm E}(f) = H(f) = 1$ is to be set. In contrast, in the range from $4 \ \rm kHz$ to $12 \ \rm kHz$ the following holds:
- $$H_{\rm E}(f)= \frac{1}{H(f)} = \frac{1}{1.5 \cdot \big[1 - f/(12\,{\rm kHz})\big]} \hspace{0.5cm} \Rightarrow \hspace{0.5cm} H_{\rm E}(f = 10\,{\rm kHz})\hspace{0.15cm}\underline{= 4} .$$
Here, the denominator expression describes the equation of the straight line of the frequency roll-off.
(7) Proposed solution 1 is correct:
- Both $x_2(t)$ and $x_3(t)$ also contain spectral components at frequencies greater than $12 \ \rm kHz$.
- If these have been truncated by $H(f)$ ⇒ band limitation, they can no longer be reconstructed by the equalizer.
- This means that only the signal $x_1(t)$ can be recovered by $H_{\rm E}(f)$ but only if $f_2 < 12 \ \rm kHz$ holds:
- $$z_1(t)= \underline{1} \cdot 1\,{\rm V}\cdot \cos(2 \pi \cdot f_1 \cdot t) + \underline{4} \cdot \frac{1}{4}\cdot 1\,{\rm V}\cdot \sin(2 \pi \cdot f_2 \cdot t).$$
- The first (underlined) factors indicate the gain values of $H_{\rm E}(f)$ respectively.