Difference between revisions of "Aufgaben:Exercise 2.6: Two-Way Channel"
From LNTwww
| (21 intermediate revisions by 2 users not shown) | |||
| Line 4: | Line 4: | ||
[[File:P_ID912__LZI_A_2_6.png|right|frame|Impulse response of the two-way channel]] | [[File:P_ID912__LZI_A_2_6.png|right|frame|Impulse response of the two-way channel]] | ||
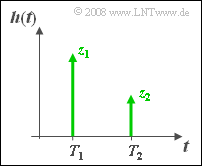
| − | The so-called two-way channel is characterised by the following impulse response $($with $T_1 < T_2)$: | + | The so-called "two-way channel" is characterised by the following impulse response $($with $T_1 < T_2)$: |
:$$h(t) = z_1 \cdot \delta ( t - T_1) + z_2 \cdot \delta ( | :$$h(t) = z_1 \cdot \delta ( t - T_1) + z_2 \cdot \delta ( | ||
t - T_2).$$ | t - T_2).$$ | ||
| − | *Except for a few combinations of the system parameters $z_1$, $T_1$, $z_2$ and $T_2$& | + | *Except for a few combinations of the system parameters $z_1$, $T_1$, $z_2$ and $T_2$, this channel will result in linear distortions. |
| − | *There is a distortion-free channel at hand only if not a single input signal is distorted by it. This means: Even if the channel is distorting, there may be special cases where indeed $y(t) = \alpha \cdot x(t - \tau)$ | + | *There is a distortion-free channel at hand only if not a single input signal is distorted by it. |
| + | *This means: Even if the two-way channel is per se distorting, there may be special cases where indeed $y(t) = \alpha \cdot x(t - \tau)$. | ||
The test signals applied to the system input are: | The test signals applied to the system input are: | ||
| − | *a [[Signal_Representation/Time_Discrete_Signal_Representation#Dirac_comb_in_time_and_frequency_domain|Dirac comb]] $x_1(t)$ at a time interval of $T_0 = 1 \ \rm ms$ whose spectral function $X_1(f)$ is also a Dirac comb with an interval of $f_0 = 1/T_0 = 1 \ \rm kHz$: | + | *a [[Signal_Representation/Time_Discrete_Signal_Representation#Dirac_comb_in_time_and_frequency_domain|Dirac comb]] $x_1(t)$ at a time interval of $T_0 = 1 \ \rm ms$, whose spectral function $X_1(f)$ is also a Dirac comb with an interval of $f_0 = 1/T_0 = 1 \ \rm kHz$: |
:$$x_1(t) = \sum_{n = - \infty}^{+\infty} \delta ( t - n \cdot T_0) ,\hspace{0.5cm} X_1(f) = T_0 \cdot \sum_{k = - \infty}^{+\infty} \delta ( f - k | :$$x_1(t) = \sum_{n = - \infty}^{+\infty} \delta ( t - n \cdot T_0) ,\hspace{0.5cm} X_1(f) = T_0 \cdot \sum_{k = - \infty}^{+\infty} \delta ( f - k | ||
\cdot f_0) ,$$ | \cdot f_0) ,$$ | ||
| Line 33: | Line 34: | ||
*The task belongs to the chapter [[Linear_and_Time_Invariant_Systems/Linear_Distortions|Linear Distortions]]. | *The task belongs to the chapter [[Linear_and_Time_Invariant_Systems/Linear_Distortions|Linear Distortions]]. | ||
| − | *To spare you calculations the result for the parameter set $\big [z_1 = 1$, $T_1 = 0$, $z_2 =0.5$, $T_2 = 1 \ \rm ms\big ]$ is given: | + | *To spare you calculations the result for the parameter set $\big [z_1 = 1$, $T_1 = 0$, $z_2 =0.5$, $T_2 = 1 \ \rm ms\big ]$ is given: |
:$$|H(f = f_2)| = |H(f = f_3)| = \sqrt{1.25} \approx 1.118, \; \; \; \; b(f = f_2) = b(f = f_3) = \arctan (0.5) \approx 0.464.$$ | :$$|H(f = f_2)| = |H(f = f_3)| = \sqrt{1.25} \approx 1.118, \; \; \; \; b(f = f_2) = b(f = f_3) = \arctan (0.5) \approx 0.464.$$ | ||
| Line 44: | Line 45: | ||
+ The parameter set $\big[z_1 = 1$, $T_1 = 0$, $z_2 =0 \big]$ is the only possible one to describe the ideal channel. | + The parameter set $\big[z_1 = 1$, $T_1 = 0$, $z_2 =0 \big]$ is the only possible one to describe the ideal channel. | ||
+ Any distortion-free channel is captured by the two combinations $\big[z_1 \ne 0, \; z_2 = 0 \big]$ or $\big[z_1 = 0, \; z_2 \ne 0 \big]$ . | + Any distortion-free channel is captured by the two combinations $\big[z_1 \ne 0, \; z_2 = 0 \big]$ or $\big[z_1 = 0, \; z_2 \ne 0 \big]$ . | ||
| − | - The values $\big[z_1 \ne 0\big]$ and $\big[z_2 \ne 0\big]$ result in a distortion-free channel if $T_1$ and $T_2$ are optimally adjusted. | + | - The values $\big[z_1 \ne 0\big]$ and $\big[z_2 \ne 0\big]$ result in a distortion-free channel if $T_1$ and $T_2$ are optimally adjusted. |
| − | { | + | {The following holds: $\big[z_1 = 1$, $T_1 = 0$, $z_2 =0.5$, $T_2 = 1 \ \rm ms\big ]$. Compute the frequency response $H(f)$ of this channel. <br>What are the values at multiples of $1 \ \rm kHz$? |
|type="{}"} | |type="{}"} | ||
${\rm Re}\big[H(f = n \cdot 1 \ {\rm kHz})\big] \ = \ $ { 1.5 3% } | ${\rm Re}\big[H(f = n \cdot 1 \ {\rm kHz})\big] \ = \ $ { 1.5 3% } | ||
| Line 53: | Line 54: | ||
| − | { | + | {The Dirac comb $x_1(t)$ is applied to the input of the system with the same parameters as in subtask '''(2)''' . <br>Which statements are true for the output signal $y_1(t)$ ? |
|type="[]"} | |type="[]"} | ||
| − | + $y_1(t)$ | + | + $y_1(t)$ is attenuated/amplified by a constant compared to $x_1(t)$ . |
| − | - $y_1(t)$ | + | - $y_1(t)$ is shifted with respect to $x_1(t)$ . |
| − | - $y_1(t)$ | + | - $y_1(t)$ exhibits distortions with respect to $x_1(t)$ . |
| − | { | + | {Compute the signal $y_2(t)$ as the system response to the cosine signal $x_2(t)$. What is the signal value at time $t = 0$ ? |
|type="{}"} | |type="{}"} | ||
$y_2(t = 0) \ = \ $ { 0.996 3% } | $y_2(t = 0) \ = \ $ { 0.996 3% } | ||
| − | { | + | {Which statements are true regarding the signals $x_3(t)$ and $y_3(t)$ ? |
|type="[]"} | |type="[]"} | ||
| − | - $y_3(t)$ | + | - $y_3(t)$ does not exhibit any distortions with respect to $x_3(t)$ . |
| − | - $y_3(t)$ | + | - $y_3(t)$ exhibits attenuation distortions with respect to $x_3(t)$ . |
| − | + $y_3(t)$ | + | + $y_3(t)$ exhibits phase distortions with respect to $x_3(t)$ . |
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' <u>Statements 1 and 2</u> are correct: |
| − | * | + | *$h(t) = \delta(t)$ is true with $z_1 = 1$, $T_1 = 0$ and $z_2 =0$ and correspondingly $H(f) = 1$ so that $y(t) = x(t)$ will always hold. |
| − | * | + | *Each distortion-free channel impulse response $h(t)$ consists of a single Dirac function, for example at $t = T_1$. |
| − | * | + | *This case is accounted for in the model by $z_2 =0$. Thus, the frequency response is: |
:$$H(f)= z_1\cdot {\rm e}^{-{\rm j}\cdot \hspace{0.05cm}2 \pi f T_1} \ \Rightarrow \ y(t) = z_1 \cdot x(t- T_1).$$ | :$$H(f)= z_1\cdot {\rm e}^{-{\rm j}\cdot \hspace{0.05cm}2 \pi f T_1} \ \Rightarrow \ y(t) = z_1 \cdot x(t- T_1).$$ | ||
| − | * | + | *In contrast, the channel will lead to linear distortions whenever $z_1$ and $z_2$ are simultaneously non-zero. |
| − | '''(2)''' | + | '''(2)''' The Fourier transform of the impulse response $h(t)$ results in the equation: |
:$$H(f) = z_1\cdot {\rm e}^{-{\rm j}\hspace{0.05cm} \cdot \hspace{0.05cm}2 \pi f T_1}+ z_2\cdot {\rm e}^{-{\rm j}\hspace{0.05cm} \cdot \hspace{0.05cm}2 \pi f T_2} | :$$H(f) = z_1\cdot {\rm e}^{-{\rm j}\hspace{0.05cm} \cdot \hspace{0.05cm}2 \pi f T_1}+ z_2\cdot {\rm e}^{-{\rm j}\hspace{0.05cm} \cdot \hspace{0.05cm}2 \pi f T_2} | ||
.$$ | .$$ | ||
| − | * | + | *The following is obtained with $z_1 = 1$, $T_1 = 0$, $z_2 =0.5$ and $T_2 = 1 \ \rm ms$: |
:$$H(f) =1 + 0.5 \cdot {\rm e}^{-{\rm j}\hspace{0.05cm} \cdot \hspace{0.05cm}2 \pi f T_2}.$$ | :$$H(f) =1 + 0.5 \cdot {\rm e}^{-{\rm j}\hspace{0.05cm} \cdot \hspace{0.05cm}2 \pi f T_2}.$$ | ||
| − | * | + | *Broken down by real and imaginary part, this yields: |
:$${\rm Re}\big[H(f)\big] = 1 + 0.5 \cdot \cos(2 \pi f \cdot 1\,{\rm ms}) \ \Rightarrow \ \underline{{\rm Re}[H(f = f_1 =1 \ \rm kHz)] = 1.5}, $$ | :$${\rm Re}\big[H(f)\big] = 1 + 0.5 \cdot \cos(2 \pi f \cdot 1\,{\rm ms}) \ \Rightarrow \ \underline{{\rm Re}[H(f = f_1 =1 \ \rm kHz)] = 1.5}, $$ | ||
:$${\rm Im}\big[H(f)\big] = -0.5 \cdot \sin(2 \pi f \cdot 1\,{\rm ms}) \ \Rightarrow \ \underline{{\rm Im}\big[H(f = f_1 =1 \ \rm kHz)\big] = 0}, $$ | :$${\rm Im}\big[H(f)\big] = -0.5 \cdot \sin(2 \pi f \cdot 1\,{\rm ms}) \ \Rightarrow \ \underline{{\rm Im}\big[H(f = f_1 =1 \ \rm kHz)\big] = 0}, $$ | ||
| − | '''(3)''' | + | '''(3)''' The <u>first answer</u> is the only correct one: |
| − | * | + | *From '''(2)''' it follows the absolute value function is $|H(f)| = 1.5$ and the phase function $b(f) \equiv 0$ for all multiples of $f_1 =1 \ \rm kHz$ ⇒ $f= n \cdot f_1$. |
| − | * | + | *Thus, the phase delay time is also zero in each case for these discrete frequency values. |
| − | * | + | *But since the spectrum $X_1(f)$ of the Dirac comb has spectral lines exactly at these frequencies, $y_1(t) = 1.5 \cdot x_1(t)$ holds. |
| − | '''(4)''' | + | '''(4)''' The absolute value function is: |
:$$|H(f)| = \sqrt{{\rm Re}[H(f)]^2 + {\rm Im}[H(f)]^2} $$ | :$$|H(f)| = \sqrt{{\rm Re}[H(f)]^2 + {\rm Im}[H(f)]^2} $$ | ||
:$$\Rightarrow \; |H(f)| = \sqrt{1 + 0.25 \cdot \cos^2(2 \pi f \cdot T_2)+ \cos(2 \pi f \cdot T_2) + 0.25 \cdot \sin^2(2 \pi f \cdot T_2)} | :$$\Rightarrow \; |H(f)| = \sqrt{1 + 0.25 \cdot \cos^2(2 \pi f \cdot T_2)+ \cos(2 \pi f \cdot T_2) + 0.25 \cdot \sin^2(2 \pi f \cdot T_2)} | ||
= \sqrt{1.25 + \cos(2 \pi f \cdot T_2) }.$$ | = \sqrt{1.25 + \cos(2 \pi f \cdot T_2) }.$$ | ||
| − | * | + | *Thus, the following is obtained for the frequency $f_2 =0.25 \ \rm kHz$: |
:$$|H(f)| = \sqrt{1.25 + \cos(\frac{\pi}{2} ) }= \sqrt{1.25} = 1.118.$$ | :$$|H(f)| = \sqrt{1.25 + \cos(\frac{\pi}{2} ) }= \sqrt{1.25} = 1.118.$$ | ||
| − | * | + | *The phase function is generally or at the frequency $f_2 =0.25 \ \rm kHz$: |
:$$b(f) = - {\rm arctan}\hspace{0.1cm}\frac{{\rm Im}[H(f)]}{{\rm | :$$b(f) = - {\rm arctan}\hspace{0.1cm}\frac{{\rm Im}[H(f)]}{{\rm | ||
Re}[H(f)]} = - {\rm arctan}\hspace{0.1cm}\frac{-0.5 \cdot \sin(2 | Re}[H(f)]} = - {\rm arctan}\hspace{0.1cm}\frac{-0.5 \cdot \sin(2 | ||
| Line 120: | Line 121: | ||
arctan}\hspace{0.1cm}\frac{0.5}{1} = 0.464.$$ | arctan}\hspace{0.1cm}\frac{0.5}{1} = 0.464.$$ | ||
| − | * | + | *Thus, the phase delay time for this frequency is: |
:$$\tau_2 = \frac {b(f_2)}{2 \pi f_2} = \frac {0.464}{2 \pi \cdot | :$$\tau_2 = \frac {b(f_2)}{2 \pi f_2} = \frac {0.464}{2 \pi \cdot | ||
| − | 0.25\,{\rm kHz}} \approx 0.3\,{\rm ms} | + | 0.25\,{\rm kHz}} \approx 0.3\,{\rm ms}.$$ |
| − | * | + | *Hence, the following holds for the output signal: |
:$$y_2(t) = 1.118 \cdot \cos(2 \pi \cdot 0.25\,{\rm kHz}\cdot (t - | :$$y_2(t) = 1.118 \cdot \cos(2 \pi \cdot 0.25\,{\rm kHz}\cdot (t - | ||
0.3\,{\rm ms})).$$ | 0.3\,{\rm ms})).$$ | ||
| − | * | + | *The signal value at zero-time is therefore: |
:$$y_2(t=0) = 1.118 \cdot \cos(-2 \pi \cdot 0.25\,{\rm kHz} \cdot | :$$y_2(t=0) = 1.118 \cdot \cos(-2 \pi \cdot 0.25\,{\rm kHz} \cdot | ||
0.3\,{\rm ms}) \approx 1.118 \cdot 0.891 \hspace{0.15cm}\underline{= 0.996}.$$ | 0.3\,{\rm ms}) \approx 1.118 \cdot 0.891 \hspace{0.15cm}\underline{= 0.996}.$$ | ||
| − | '''(5)''' | + | '''(5)''' Both frequencies have the same attenuation factor $\alpha = 1.118$ . Therefore, no attenuation distortions are observed. |
| − | * | + | *The following is obtained for the phase function with $f_3 = 1.25 \ \rm kHz$ and $T_2 = 1 \ \rm ms$ : |
:$$b(f = f_3) = - {\rm arctan}\hspace{0.1cm}\frac{-0.5 \cdot \sin( | :$$b(f = f_3) = - {\rm arctan}\hspace{0.1cm}\frac{-0.5 \cdot \sin( | ||
2.5 \pi)}{1+0.5 \cdot \cos(2.5 \pi)}= 0.464 = b(f = f_2),$$ | 2.5 \pi)}{1+0.5 \cdot \cos(2.5 \pi)}= 0.464 = b(f = f_2),$$ | ||
| − | : | + | :so exactly the same value as for the frequency $f_2 = 0.25 \ \rm kHz$. |
| − | * | + | *Despite this, however, phase distortions now occur since for $f_3$ the phase delay time is only $\tau = 60 \ µ \rm s$ anymore. |
| − | * | + | *So, the following can be formulated for the output signal: |
:$$y_3(t) = 1.118 \cdot \cos(2 \pi f_2 \cdot (t - 0.3\,{\rm ms}) + | :$$y_3(t) = 1.118 \cdot \cos(2 \pi f_2 \cdot (t - 0.3\,{\rm ms}) + | ||
1.118 | 1.118 | ||
| Line 149: | Line 150: | ||
\cos(2 \pi f_3 \cdot t - 27^\circ).$$ | \cos(2 \pi f_3 \cdot t - 27^\circ).$$ | ||
| − | + | Accordingly, the correct <u>answer is 3</u>: | |
| − | * | + | *So, there are phase distortions although for both oscillations, $\varphi_2 = \varphi_3= 27^\circ$ holds. |
| − | * | + | *To avoid phase distortions |
| − | ** | + | **the phase delay times $\tau_2$ and $\tau_3$ would have to be equal and |
| − | ** | + | **the phase values $\varphi_2$ and $\varphi_3$ would have to increase linearly with the corresponding frequencies. |
{{ML-Fuß}} | {{ML-Fuß}} | ||
| − | [[Category:Linear and Time-Invariant Systems: Exercises|^2.3 | + | [[Category:Linear and Time-Invariant Systems: Exercises|^2.3 Linear Distortions^]] |
Latest revision as of 10:29, 6 October 2021
The so-called "two-way channel" is characterised by the following impulse response $($with $T_1 < T_2)$:
- $$h(t) = z_1 \cdot \delta ( t - T_1) + z_2 \cdot \delta ( t - T_2).$$
- Except for a few combinations of the system parameters $z_1$, $T_1$, $z_2$ and $T_2$, this channel will result in linear distortions.
- There is a distortion-free channel at hand only if not a single input signal is distorted by it.
- This means: Even if the two-way channel is per se distorting, there may be special cases where indeed $y(t) = \alpha \cdot x(t - \tau)$.
The test signals applied to the system input are:
- a Dirac comb $x_1(t)$ at a time interval of $T_0 = 1 \ \rm ms$, whose spectral function $X_1(f)$ is also a Dirac comb with an interval of $f_0 = 1/T_0 = 1 \ \rm kHz$:
- $$x_1(t) = \sum_{n = - \infty}^{+\infty} \delta ( t - n \cdot T_0) ,\hspace{0.5cm} X_1(f) = T_0 \cdot \sum_{k = - \infty}^{+\infty} \delta ( f - k \cdot f_0) ,$$
- a cosine signal with frequency $f_2 = 250 \ \rm Hz$:
- $$x_2(t) = \cos(2 \pi \cdot f_2 \cdot t) ,$$
- the sum of two cosine signals with frequencies $f_2 = 250 \ \rm Hz$ and $f_3 = 1250 \ \rm Hz$:
- $$x_3(t) = \cos(2 \pi \cdot f_2 \cdot t) + \cos(2 \pi \cdot f_3 \cdot t) .$$
Please note:
- The task belongs to the chapter Linear Distortions.
- To spare you calculations the result for the parameter set $\big [z_1 = 1$, $T_1 = 0$, $z_2 =0.5$, $T_2 = 1 \ \rm ms\big ]$ is given:
- $$|H(f = f_2)| = |H(f = f_3)| = \sqrt{1.25} \approx 1.118, \; \; \; \; b(f = f_2) = b(f = f_3) = \arctan (0.5) \approx 0.464.$$
Questions
Solution
(1) Statements 1 and 2 are correct:
- $h(t) = \delta(t)$ is true with $z_1 = 1$, $T_1 = 0$ and $z_2 =0$ and correspondingly $H(f) = 1$ so that $y(t) = x(t)$ will always hold.
- Each distortion-free channel impulse response $h(t)$ consists of a single Dirac function, for example at $t = T_1$.
- This case is accounted for in the model by $z_2 =0$. Thus, the frequency response is:
- $$H(f)= z_1\cdot {\rm e}^{-{\rm j}\cdot \hspace{0.05cm}2 \pi f T_1} \ \Rightarrow \ y(t) = z_1 \cdot x(t- T_1).$$
- In contrast, the channel will lead to linear distortions whenever $z_1$ and $z_2$ are simultaneously non-zero.
(2) The Fourier transform of the impulse response $h(t)$ results in the equation:
- $$H(f) = z_1\cdot {\rm e}^{-{\rm j}\hspace{0.05cm} \cdot \hspace{0.05cm}2 \pi f T_1}+ z_2\cdot {\rm e}^{-{\rm j}\hspace{0.05cm} \cdot \hspace{0.05cm}2 \pi f T_2} .$$
- The following is obtained with $z_1 = 1$, $T_1 = 0$, $z_2 =0.5$ and $T_2 = 1 \ \rm ms$:
- $$H(f) =1 + 0.5 \cdot {\rm e}^{-{\rm j}\hspace{0.05cm} \cdot \hspace{0.05cm}2 \pi f T_2}.$$
- Broken down by real and imaginary part, this yields:
- $${\rm Re}\big[H(f)\big] = 1 + 0.5 \cdot \cos(2 \pi f \cdot 1\,{\rm ms}) \ \Rightarrow \ \underline{{\rm Re}[H(f = f_1 =1 \ \rm kHz)] = 1.5}, $$
- $${\rm Im}\big[H(f)\big] = -0.5 \cdot \sin(2 \pi f \cdot 1\,{\rm ms}) \ \Rightarrow \ \underline{{\rm Im}\big[H(f = f_1 =1 \ \rm kHz)\big] = 0}, $$
(3) The first answer is the only correct one:
- From (2) it follows the absolute value function is $|H(f)| = 1.5$ and the phase function $b(f) \equiv 0$ for all multiples of $f_1 =1 \ \rm kHz$ ⇒ $f= n \cdot f_1$.
- Thus, the phase delay time is also zero in each case for these discrete frequency values.
- But since the spectrum $X_1(f)$ of the Dirac comb has spectral lines exactly at these frequencies, $y_1(t) = 1.5 \cdot x_1(t)$ holds.
(4) The absolute value function is:
- $$|H(f)| = \sqrt{{\rm Re}[H(f)]^2 + {\rm Im}[H(f)]^2} $$
- $$\Rightarrow \; |H(f)| = \sqrt{1 + 0.25 \cdot \cos^2(2 \pi f \cdot T_2)+ \cos(2 \pi f \cdot T_2) + 0.25 \cdot \sin^2(2 \pi f \cdot T_2)} = \sqrt{1.25 + \cos(2 \pi f \cdot T_2) }.$$
- Thus, the following is obtained for the frequency $f_2 =0.25 \ \rm kHz$:
- $$|H(f)| = \sqrt{1.25 + \cos(\frac{\pi}{2} ) }= \sqrt{1.25} = 1.118.$$
- The phase function is generally or at the frequency $f_2 =0.25 \ \rm kHz$:
- $$b(f) = - {\rm arctan}\hspace{0.1cm}\frac{{\rm Im}[H(f)]}{{\rm Re}[H(f)]} = - {\rm arctan}\hspace{0.1cm}\frac{-0.5 \cdot \sin(2 \pi f T_2)}{1+0.5 \cdot \cos(2 \pi f T_2)},$$
- $$b(f = f_2) = - {\rm arctan}\hspace{0.1cm}\frac{-0.5 \cdot \sin( \pi/2)}{1+0.5 \cdot \cos(\pi/2)}={\rm arctan}\hspace{0.1cm}\frac{0.5}{1} = 0.464.$$
- Thus, the phase delay time for this frequency is:
- $$\tau_2 = \frac {b(f_2)}{2 \pi f_2} = \frac {0.464}{2 \pi \cdot 0.25\,{\rm kHz}} \approx 0.3\,{\rm ms}.$$
- Hence, the following holds for the output signal:
- $$y_2(t) = 1.118 \cdot \cos(2 \pi \cdot 0.25\,{\rm kHz}\cdot (t - 0.3\,{\rm ms})).$$
- The signal value at zero-time is therefore:
- $$y_2(t=0) = 1.118 \cdot \cos(-2 \pi \cdot 0.25\,{\rm kHz} \cdot 0.3\,{\rm ms}) \approx 1.118 \cdot 0.891 \hspace{0.15cm}\underline{= 0.996}.$$
(5) Both frequencies have the same attenuation factor $\alpha = 1.118$ . Therefore, no attenuation distortions are observed.
- The following is obtained for the phase function with $f_3 = 1.25 \ \rm kHz$ and $T_2 = 1 \ \rm ms$ :
- $$b(f = f_3) = - {\rm arctan}\hspace{0.1cm}\frac{-0.5 \cdot \sin( 2.5 \pi)}{1+0.5 \cdot \cos(2.5 \pi)}= 0.464 = b(f = f_2),$$
- so exactly the same value as for the frequency $f_2 = 0.25 \ \rm kHz$.
- Despite this, however, phase distortions now occur since for $f_3$ the phase delay time is only $\tau = 60 \ µ \rm s$ anymore.
- So, the following can be formulated for the output signal:
- $$y_3(t) = 1.118 \cdot \cos(2 \pi f_2 \cdot (t - 0.3\,{\rm ms}) + 1.118 \cdot \cos(2 \pi f_3 \cdot (t - 0.06\,{\rm ms})$$
- $$\Rightarrow \; \; y_3(t) = 1.118 \cdot \cos(2 \pi f_2 \cdot t - 27^\circ) + 1.118 \cdot \cos(2 \pi f_3 \cdot t - 27^\circ).$$
Accordingly, the correct answer is 3:
- So, there are phase distortions although for both oscillations, $\varphi_2 = \varphi_3= 27^\circ$ holds.
- To avoid phase distortions
- the phase delay times $\tau_2$ and $\tau_3$ would have to be equal and
- the phase values $\varphi_2$ and $\varphi_3$ would have to increase linearly with the corresponding frequencies.