Difference between revisions of "Aufgaben:Exercise 4.2: Triangular PDF"
From LNTwww
m (Text replacement - "[[Informationstheorie" to "[[Information_Theory") |
m (Text replacement - "value-continuous" to "continuous") |
||
| (10 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Information_Theory/Differential_Entropy |
}} | }} | ||
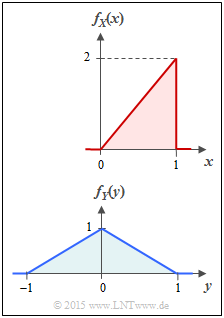
| − | [[File:P_ID2865__Inf_A_4_2.png|right|frame| | + | [[File:P_ID2865__Inf_A_4_2.png|right|frame|Two triangular PDFs]] |
| − | + | Two probability density functions $\rm (PDF)$ with triangular shapes are considered. | |
| − | * | + | * The random variable $X$ is limited to the range from $0$ to $1$ , and it holds for the PDF (upper sketch): |
| − | :$$f_X(x) = \left\{ \begin{array}{c} 2x \\ 0 \\ \end{array} \right. \begin{array}{*{20}c} {\rm{f\ddot{u}r}} \hspace{0.1cm} 0 \le x \le 1 \\ {\rm | + | :$$f_X(x) = \left\{ \begin{array}{c} 2x \\ 0 \\ \end{array} \right. \begin{array}{*{20}c} {\rm{f\ddot{u}r}} \hspace{0.1cm} 0 \le x \le 1 \\ {\rm else} \\ \end{array} |
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | * | + | * According to the lower sketch, the random variable $Y$ has the following PDF: |
| − | :$$f_Y(y) = \left\{ \begin{array}{c} 1 - |\hspace{0.03cm}y\hspace{0.03cm}| \\ 0 \\ \end{array} \right. \begin{array}{*{20}c} {\rm{f\ddot{u}r}} \hspace{0.1cm} |\hspace{0.03cm}y\hspace{0.03cm}| \le 1 \\ {\rm | + | :$$f_Y(y) = \left\{ \begin{array}{c} 1 - |\hspace{0.03cm}y\hspace{0.03cm}| \\ 0 \\ \end{array} \right. \begin{array}{*{20}c} {\rm{f\ddot{u}r}} \hspace{0.1cm} |\hspace{0.03cm}y\hspace{0.03cm}| \le 1 \\ {\rm else} \\ \end{array} |
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | + | For both random variables, the [[Information_Theory/Differentielle_Entropie|differential entropy]] is to be determined in each case. | |
| − | + | For example, the corresponding equation for the random variable $X$ is: | |
:$$h(X) = | :$$h(X) = | ||
\hspace{0.1cm} - \hspace{-0.45cm} \int\limits_{{\rm supp}\hspace{0.03cm}(\hspace{-0.03cm}f_X)} \hspace{-0.35cm} f_X(x) \cdot {\rm log} \hspace{0.1cm} \big [ f_X(x) \big ] \hspace{0.1cm}{\rm d}x | \hspace{0.1cm} - \hspace{-0.45cm} \int\limits_{{\rm supp}\hspace{0.03cm}(\hspace{-0.03cm}f_X)} \hspace{-0.35cm} f_X(x) \cdot {\rm log} \hspace{0.1cm} \big [ f_X(x) \big ] \hspace{0.1cm}{\rm d}x | ||
| − | \hspace{0.6cm}{\rm | + | \hspace{0.6cm}{\rm with}\hspace{0.6cm} {\rm supp}(f_X) = \{ x\text{:} \ f_X(x) > 0 \} |
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | * | + | *If the "natural logarithm", the pseudo-unit "nat" must be added. |
| − | * | + | *If, on the other hand, the result is asked in "bit" then the "dual logarithm" ⇒ "$\log_2$" is to be used. |
| − | In | + | In the fourth subtask, the new random variable $Z = A \cdot Y$ is considered. Here, the PDF parameter $A$ is to be determined in such a way that the differential entropy of the new random variable $Z$ yields exactly $1$ bit :<br> |
| − | :$$h(Z) = h (A \cdot Y) = h (Y) + {\rm log}_2 \hspace{0.1cm} (A) = 1\ | + | :$$h(Z) = h (A \cdot Y) = h (Y) + {\rm log}_2 \hspace{0.1cm} (A) = 1\ {\rm bit} \hspace{0.05cm}.$$ |
| Line 32: | Line 32: | ||
| − | + | Hints: | |
| − | * | + | *The task belongs to the chapter [[Information_Theory/Differentielle_Entropie|Differential Entropy]]. |
| − | * | + | *Useful hints for solving this task and further information on continuous random variables can be found in the third chapter "Continuous Random Variables" of the book [[Theory of Stochastic Signals]]. |
| − | * | + | *Given the following indefinite integral: |
:$$\int \xi \cdot {\rm ln} \hspace{0.1cm} (\xi)\hspace{0.1cm}{\rm d}\xi = | :$$\int \xi \cdot {\rm ln} \hspace{0.1cm} (\xi)\hspace{0.1cm}{\rm d}\xi = | ||
\xi^2 \cdot \big [1/2 \cdot {{\rm ln} \hspace{0.1cm} (\xi)} - | \xi^2 \cdot \big [1/2 \cdot {{\rm ln} \hspace{0.1cm} (\xi)} - | ||
| Line 43: | Line 43: | ||
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Calculate the differential entropy of the random variable $X$ in "nat". |
|type="{}"} | |type="{}"} | ||
$h(X) \ = \ $ { -0.199--0.187 } $\ \rm nat$ | $h(X) \ = \ $ { -0.199--0.187 } $\ \rm nat$ | ||
| − | { | + | {What result is obtained with the pseudo-unit "bit"? |
|type="{}"} | |type="{}"} | ||
$h(X) \ = \ $ { -0.288--0.270 } $\ \rm bit$ | $h(X) \ = \ $ { -0.288--0.270 } $\ \rm bit$ | ||
| − | { | + | {Calculate the differential entropy of the random variable $Y$. |
|type="{}"} | |type="{}"} | ||
$h(Y) \ = \ $ { 0.721 3% } $\ \rm bit$ | $h(Y) \ = \ $ { 0.721 3% } $\ \rm bit$ | ||
| − | { | + | {Determine the PDF parameter $A$ such that $\underline{h(Z) = h (A \cdot Y) = 1 \ \rm bit}$ . |
|type="{}"} | |type="{}"} | ||
$A\ = $ { 1.213 3% } | $A\ = $ { 1.213 3% } | ||
| Line 65: | Line 65: | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' For the probability density function, in the range $0 \le X \le 1$ , it is agreed that: |
:$$f_X(x) = 2x = C \cdot x | :$$f_X(x) = 2x = C \cdot x | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | * | + | *Here we have replaced "2" by $C$ ⇒ generalization in order to be able to use the following calculation again in subtask $(3)$ . |
| − | * | + | *Since the differential entropy is sought in "nat", we use the natural logarithm. With the substitution $\xi = C \cdot x$ we obtain: |
:$$h_{\rm nat}(X) = \hspace{0.1cm} - \int_{0}^{1} \hspace{0.1cm} C \cdot x \cdot {\rm ln} \hspace{0.1cm} \big[ C \cdot x \big] \hspace{0.1cm}{\rm d}x = | :$$h_{\rm nat}(X) = \hspace{0.1cm} - \int_{0}^{1} \hspace{0.1cm} C \cdot x \cdot {\rm ln} \hspace{0.1cm} \big[ C \cdot x \big] \hspace{0.1cm}{\rm d}x = | ||
\hspace{0.1cm} - \hspace{0.1cm}\frac{1}{C} \cdot \int_{0}^{C} \hspace{0.1cm} \xi \cdot {\rm ln} \hspace{0.1cm} [ \xi ] \hspace{0.1cm}{\rm d}\xi | \hspace{0.1cm} - \hspace{0.1cm}\frac{1}{C} \cdot \int_{0}^{C} \hspace{0.1cm} \xi \cdot {\rm ln} \hspace{0.1cm} [ \xi ] \hspace{0.1cm}{\rm d}\xi | ||
| Line 79: | Line 79: | ||
\frac{1}{4}\right ]_{\xi = 0}^{\xi = C} | \frac{1}{4}\right ]_{\xi = 0}^{\xi = C} | ||
\hspace{0.05cm}$$ | \hspace{0.05cm}$$ | ||
| − | * | + | *Here the indefinite integral given in the front was used. After inserting the limits, considering $C=2$, we obtain:: |
:$$h_{\rm nat}(X) = | :$$h_{\rm nat}(X) = | ||
- C/2 \cdot | - C/2 \cdot | ||
| Line 95: | Line 95: | ||
| − | '''(2)''' | + | '''(2)''' In general: |
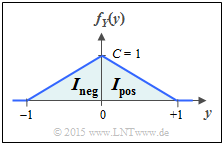
| + | [[File:P_ID2866__Inf_A_4_2c.png|right|frame|To calculate $h(Y)$]] | ||
| + | |||
:$$h_{\rm bit}(X) = \frac{h_{\rm nat}(X)}{{\rm ln} \hspace{0.1cm} (2)\,{\rm nat/bit}} = - 0.279 | :$$h_{\rm bit}(X) = \frac{h_{\rm nat}(X)}{{\rm ln} \hspace{0.1cm} (2)\,{\rm nat/bit}} = - 0.279 | ||
\hspace{0.3cm} \Rightarrow\hspace{0.3cm} | \hspace{0.3cm} \Rightarrow\hspace{0.3cm} | ||
| Line 101: | Line 103: | ||
\hspace{0.15cm}\underline {= - 0.279\,{\rm bit}} | \hspace{0.15cm}\underline {= - 0.279\,{\rm bit}} | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | * | + | *You can save this conversion if you directly replace $(1)$ direct "ln" by "log<sub>2</sub>" already in the analytical result of subtask: |
| + | |||
:$$h(X) = \ {\rm log}_2 \hspace{0.1cm} (\sqrt{\rm e}/2)\hspace{0.05cm}, \hspace{1.3cm} | :$$h(X) = \ {\rm log}_2 \hspace{0.1cm} (\sqrt{\rm e}/2)\hspace{0.05cm}, \hspace{1.3cm} | ||
| − | {\rm | + | {\rm pseudo-unit\hspace{-0.1cm}:\hspace{0.15cm} bit} |
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | + | '''(3)''' We again use the natural logarithm and divide the integral into two partial integrals: | |
| − | '''(3)''' | ||
:$$h(Y) = | :$$h(Y) = | ||
\hspace{0.1cm} - \hspace{-0.45cm} \int\limits_{{\rm supp} | \hspace{0.1cm} - \hspace{-0.45cm} \int\limits_{{\rm supp} | ||
| Line 115: | Line 117: | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | * | + | *The first integral for the range $-1 \le y \le 0$ is identical in form to that of subtask $(1)$ and only shifted with respect to it, which does not affect the result. |
| − | * | + | *Now the height $C = 1$ instead of $C = 2$ has to be considered: |
:$$I_{\rm neg} =- C/2 \cdot | :$$I_{\rm neg} =- C/2 \cdot | ||
\big [ {\rm ln} \hspace{0.1cm} (C) - 1/2 | \big [ {\rm ln} \hspace{0.1cm} (C) - 1/2 | ||
| Line 124: | Line 126: | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | * | + | *The second integrand is identical to the first except for a shift and reflection. Moreover, the integration intervals do not overlap ⇒ $I_{\rm pos} = I_{\rm neg}$: |
:$$h_{\rm nat}(Y) = 2 \cdot I_{\rm neg} = 1/2 \cdot | :$$h_{\rm nat}(Y) = 2 \cdot I_{\rm neg} = 1/2 \cdot | ||
{\rm ln} \hspace{0.1cm} ({\rm e}) = {\rm ln} \hspace{0.1cm} (\sqrt{\rm e}) \hspace{0.3cm} | {\rm ln} \hspace{0.1cm} ({\rm e}) = {\rm ln} \hspace{0.1cm} (\sqrt{\rm e}) \hspace{0.3cm} | ||
| Line 133: | Line 135: | ||
| − | '''(4)''' | + | '''(4)''' For the differential entropy of the random variable $Z = A \cdot Y$ holds in general: |
:$$h(Z) = h(A \cdot Y) = h(Y) + {\rm log}_2 \hspace{0.1cm} (A) \hspace{0.05cm}.$$ | :$$h(Z) = h(A \cdot Y) = h(Y) + {\rm log}_2 \hspace{0.1cm} (A) \hspace{0.05cm}.$$ | ||
| − | * | + | *Thus, from the requiremen $h(Z) = 1 \ \rm bit$ and the result of subtask $(3)$ follows: |
:$${\rm log}_2 \hspace{0.1cm} (A) = 1\,{\rm bit} - 0.721 \,{\rm bit} = 0.279 \,{\rm bit} | :$${\rm log}_2 \hspace{0.1cm} (A) = 1\,{\rm bit} - 0.721 \,{\rm bit} = 0.279 \,{\rm bit} | ||
\hspace{0.3cm} \Rightarrow\hspace{0.3cm} A = 2^{0.279}\hspace{0.15cm}\underline | \hspace{0.3cm} \Rightarrow\hspace{0.3cm} A = 2^{0.279}\hspace{0.15cm}\underline | ||
| Line 144: | Line 146: | ||
| − | [[Category: | + | [[Category:Information Theory: Exercises|^4.1 Differential Entropy^]] |
Latest revision as of 09:27, 11 October 2021
Two probability density functions $\rm (PDF)$ with triangular shapes are considered.
- The random variable $X$ is limited to the range from $0$ to $1$ , and it holds for the PDF (upper sketch):
- $$f_X(x) = \left\{ \begin{array}{c} 2x \\ 0 \\ \end{array} \right. \begin{array}{*{20}c} {\rm{f\ddot{u}r}} \hspace{0.1cm} 0 \le x \le 1 \\ {\rm else} \\ \end{array} \hspace{0.05cm}.$$
- According to the lower sketch, the random variable $Y$ has the following PDF:
- $$f_Y(y) = \left\{ \begin{array}{c} 1 - |\hspace{0.03cm}y\hspace{0.03cm}| \\ 0 \\ \end{array} \right. \begin{array}{*{20}c} {\rm{f\ddot{u}r}} \hspace{0.1cm} |\hspace{0.03cm}y\hspace{0.03cm}| \le 1 \\ {\rm else} \\ \end{array} \hspace{0.05cm}.$$
For both random variables, the differential entropy is to be determined in each case.
For example, the corresponding equation for the random variable $X$ is:
- $$h(X) = \hspace{0.1cm} - \hspace{-0.45cm} \int\limits_{{\rm supp}\hspace{0.03cm}(\hspace{-0.03cm}f_X)} \hspace{-0.35cm} f_X(x) \cdot {\rm log} \hspace{0.1cm} \big [ f_X(x) \big ] \hspace{0.1cm}{\rm d}x \hspace{0.6cm}{\rm with}\hspace{0.6cm} {\rm supp}(f_X) = \{ x\text{:} \ f_X(x) > 0 \} \hspace{0.05cm}.$$
- If the "natural logarithm", the pseudo-unit "nat" must be added.
- If, on the other hand, the result is asked in "bit" then the "dual logarithm" ⇒ "$\log_2$" is to be used.
In the fourth subtask, the new random variable $Z = A \cdot Y$ is considered. Here, the PDF parameter $A$ is to be determined in such a way that the differential entropy of the new random variable $Z$ yields exactly $1$ bit :
- $$h(Z) = h (A \cdot Y) = h (Y) + {\rm log}_2 \hspace{0.1cm} (A) = 1\ {\rm bit} \hspace{0.05cm}.$$
Hints:
- The task belongs to the chapter Differential Entropy.
- Useful hints for solving this task and further information on continuous random variables can be found in the third chapter "Continuous Random Variables" of the book Theory of Stochastic Signals.
- Given the following indefinite integral:
- $$\int \xi \cdot {\rm ln} \hspace{0.1cm} (\xi)\hspace{0.1cm}{\rm d}\xi = \xi^2 \cdot \big [1/2 \cdot {{\rm ln} \hspace{0.1cm} (\xi)} - {1}/{4}\big ] \hspace{0.05cm}.$$
Questions
Solution
(1) For the probability density function, in the range $0 \le X \le 1$ , it is agreed that:
- $$f_X(x) = 2x = C \cdot x \hspace{0.05cm}.$$
- Here we have replaced "2" by $C$ ⇒ generalization in order to be able to use the following calculation again in subtask $(3)$ .
- Since the differential entropy is sought in "nat", we use the natural logarithm. With the substitution $\xi = C \cdot x$ we obtain:
- $$h_{\rm nat}(X) = \hspace{0.1cm} - \int_{0}^{1} \hspace{0.1cm} C \cdot x \cdot {\rm ln} \hspace{0.1cm} \big[ C \cdot x \big] \hspace{0.1cm}{\rm d}x = \hspace{0.1cm} - \hspace{0.1cm}\frac{1}{C} \cdot \int_{0}^{C} \hspace{0.1cm} \xi \cdot {\rm ln} \hspace{0.1cm} [ \xi ] \hspace{0.1cm}{\rm d}\xi = - \hspace{0.1cm}\frac{\xi^2}{C} \cdot \left [ \frac{{\rm ln} \hspace{0.1cm} (\xi)}{2} - \frac{1}{4}\right ]_{\xi = 0}^{\xi = C} \hspace{0.05cm}$$
- Here the indefinite integral given in the front was used. After inserting the limits, considering $C=2$, we obtain::
- $$h_{\rm nat}(X) = - C/2 \cdot \big [ {\rm ln} \hspace{0.1cm} (C) - 1/2 \big ] = - {\rm ln} \hspace{0.1cm} (2) + 1/2 = - {\rm ln} \hspace{0.1cm} (2) + 1/2 \cdot {\rm ln} \hspace{0.1cm} ({\rm e}) = {\rm ln} \hspace{0.1cm} (\sqrt{\rm e}/2)\hspace{0.05cm} = - 0.193 \hspace{0.3cm} \Rightarrow\hspace{0.3cm} h(X) \hspace{0.15cm}\underline {= - 0.193\,{\rm nat}} \hspace{0.05cm}.$$
(2) In general:
- $$h_{\rm bit}(X) = \frac{h_{\rm nat}(X)}{{\rm ln} \hspace{0.1cm} (2)\,{\rm nat/bit}} = - 0.279 \hspace{0.3cm} \Rightarrow\hspace{0.3cm} h(X) \hspace{0.15cm}\underline {= - 0.279\,{\rm bit}} \hspace{0.05cm}.$$
- You can save this conversion if you directly replace $(1)$ direct "ln" by "log2" already in the analytical result of subtask:
- $$h(X) = \ {\rm log}_2 \hspace{0.1cm} (\sqrt{\rm e}/2)\hspace{0.05cm}, \hspace{1.3cm} {\rm pseudo-unit\hspace{-0.1cm}:\hspace{0.15cm} bit} \hspace{0.05cm}.$$
(3) We again use the natural logarithm and divide the integral into two partial integrals:
- $$h(Y) = \hspace{0.1cm} - \hspace{-0.45cm} \int\limits_{{\rm supp} \hspace{0.03cm}( \hspace{-0.03cm}f_Y)} \hspace{-0.35cm} f_Y(y) \cdot {\rm ln} \hspace{0.1cm} \big[ f_Y(y) \big] \hspace{0.1cm}{\rm d}y = I_{\rm neg} + I_{\rm pos} \hspace{0.05cm}.$$
- The first integral for the range $-1 \le y \le 0$ is identical in form to that of subtask $(1)$ and only shifted with respect to it, which does not affect the result.
- Now the height $C = 1$ instead of $C = 2$ has to be considered:
- $$I_{\rm neg} =- C/2 \cdot \big [ {\rm ln} \hspace{0.1cm} (C) - 1/2 \big ] = -1/2 \cdot \big [ {\rm ln} \hspace{0.1cm} (1) - 1/2 \cdot {\rm ln} \hspace{0.1cm} ({\rm e}) \big ]= 1/4 \cdot {\rm ln} \hspace{0.1cm} ({\rm e}) \hspace{0.05cm}.$$
- The second integrand is identical to the first except for a shift and reflection. Moreover, the integration intervals do not overlap ⇒ $I_{\rm pos} = I_{\rm neg}$:
- $$h_{\rm nat}(Y) = 2 \cdot I_{\rm neg} = 1/2 \cdot {\rm ln} \hspace{0.1cm} ({\rm e}) = {\rm ln} \hspace{0.1cm} (\sqrt{\rm e}) \hspace{0.3cm} \Rightarrow\hspace{0.3cm}h_{\rm bit}(Y) = {\rm log}_2 \hspace{0.1cm} (\sqrt{\rm e}) \hspace{0.3cm} \Rightarrow\hspace{0.3cm} h(Y) = {\rm log}_2 \hspace{0.1cm} (1.649)\hspace{0.15cm}\underline {= 0.721\,{\rm bit}}\hspace{0.05cm}.$$
(4) For the differential entropy of the random variable $Z = A \cdot Y$ holds in general:
- $$h(Z) = h(A \cdot Y) = h(Y) + {\rm log}_2 \hspace{0.1cm} (A) \hspace{0.05cm}.$$
- Thus, from the requiremen $h(Z) = 1 \ \rm bit$ and the result of subtask $(3)$ follows:
- $${\rm log}_2 \hspace{0.1cm} (A) = 1\,{\rm bit} - 0.721 \,{\rm bit} = 0.279 \,{\rm bit} \hspace{0.3cm} \Rightarrow\hspace{0.3cm} A = 2^{0.279}\hspace{0.15cm}\underline {= 1.213} \hspace{0.05cm}.$$