Difference between revisions of "Aufgaben:Exercise 1.2Z: Puls Code Modulation"
From LNTwww
| (36 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Signal_Representation/Signal_classification}} |
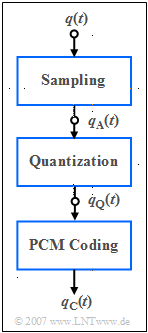
| − | [[File: | + | [[File:EN_Sig_Z_1_2.png|right|frame|PCM components]] |
| − | + | All modern communication systems are digital. The principle of digital transmission of speech signals goes back to [https://en.wikipedia.org/wiki/Alec_Reeves Alec Reeves], who invented the so-called "Puls Code Modulation" $\rm (PCM)$ as early as 1938. | |
| − | + | On the right you see the (simplified) block diagram of the PCM transmitter with three functional units: | |
| − | * | + | *The band-limited speech signal ${q(t)}$ is sampled, where the [[Signal_Representation/Time_Discrete_Signal_Representation#The_Sampling_Theorem|Sampling Theorem]] is observed, and yields the sampled signal $q_{\rm A}(t)$. |
| − | * | + | * Each sample $q_{\rm A}(t)$ is mapped to one of $M = 2^N$ results in the quantized signal $q_{\rm Q}(t)$. |
| − | * | + | * Each individual quantized value is represented by a code sequence of $N$ binary symbols and results in the coded signal $q_{\rm C}(t)$. |
| − | In | + | In this task only the different signals of the PCM transmitter are to be classified. <br>Later tasks will deal with other properties of the puls code modulation. |
| − | |||
| − | === | + | |
| + | ''Note:'' This task belongs to the chapter [[Signal_Representation/Signal_classification|Signal classification]]. | ||
| + | |||
| + | |||
| + | |||
| + | ===Questions=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Which of the statements are true for the source signal ${q(t)}$ ? |
|type="[]"} | |type="[]"} | ||
| − | + | + | + In normal operation ${q(t)}$ is a stochastic signal. |
| − | + | + | + A deterministic source signal is only useful in test operation or for theoretical investigations. |
| − | - ${q(t)}$ | + | - ${q(t)}$ is a discrete-time signal. |
| − | + ${q(t)}$ | + | + ${q(t)}$ is a continuous-valued signal. |
| − | { | + | {Which of the statements apply to the sampled signal $q_{\rm A}(t)$ ? |
|type="[]"} | |type="[]"} | ||
| − | - $q_{\rm A}(t)$ | + | - $q_{\rm A}(t)$ is a discrete-valued signal. |
| − | + $q_{\rm A}(t)$ | + | + $q_{\rm A}(t)$ is a discrete-time signal. |
| − | + | + | + The higher the maximum frequency of the source signal, the higher the sampling rate must be selected. |
| − | { | + | {Which statements are true for the quantized signal $q_{\rm Q}(t)$ if $N = 8$ is taken as a base? |
|type="[]"} | |type="[]"} | ||
| − | + $q_{\rm Q}(t)$ | + | + $q_{\rm Q}(t)$ is a discrete-time signal. |
| − | - $q_{\rm Q}(t)$ | + | - $q_{\rm Q}(t)$ is a discrete-valued signal with $M = 8$ possible values. |
| − | + $q_{\rm Q}(t)$ | + | + $q_{\rm Q}(t)$ is a discrete-valued signal with $M = 256$ possible values. |
| − | - $q_{\rm Q}(t)$ | + | - $q_{\rm Q}(t)$ is a binary signal. |
| − | { | + | {Which statements are true for the coded signal $q_{\rm C}(t)$ if $N = 8$ is taken as a base? |
|type="[]"} | |type="[]"} | ||
| − | + $q_{\rm C}(t)$ | + | + $q_{\rm C}(t)$ is a discrete-time signal. |
| − | - $q_{\rm C}(t)$ | + | - $q_{\rm C}(t)$ is a discrete-time signal with $M = 8$ possible values. |
| − | + $q_{\rm C}(t)$ | + | + $q_{\rm C}(t)$ is a binary signal. |
| − | - | + | - When sampling at distance $T_{\rm A}$ the bit duration is $T_{\rm B} = T_{\rm A}$. |
| − | + | + | + When sampling at distance $T_{\rm A}$ the bit duration is $T_{\rm B} = T_{\rm A}/8$. |
| Line 56: | Line 60: | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' Correct are the <u>solutions 1, 2 and 4</u>: |
| − | * | + | *The source signal ${q(t)}$ is analog, i.e. "continuous in time and value". |
| − | * | + | *In general, it makes no sense to transmit a deterministic signal. |
| − | * | + | *For the mathematical description, a deterministic source signal – such as a periodic signal – is better suited than a random signal. |
| − | * | + | *Deterministic signals are also used for testing in order to be able to reconstruct detected errors. |
| + | |||
| + | |||
| + | |||
| + | '''(2)''' Correct are the <u>solution suggestions 2 and 3</u>: | ||
| + | *After sampling, the signal $q_{\rm A}(t)$ is still continuous in value, but now also discrete in time. | ||
| + | *The sampling frequency $f_{\rm A}$ is given by the so-called "Sampling Theorem". | ||
| + | *The greater the maximum frequency $f_{\rm N,\,max}$ of the source signal, the greater must $f_{\rm A} ≥ 2 \cdot f_{\rm N,\,max}$ be selected. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| + | '''(3)''' Correct are the <u>solution suggestions 1 and 3</u>: | ||
| + | *The quantized signal $q_{\rm Q}(t)$ is discrete in time and value, where the number of levels are $M = 2^8 = 256$ . | ||
| + | *A binary signal, on the other hand, is a discrete-valued signal with the level number $M = 2$. | ||
| − | |||
| − | |||
| − | |||
| − | '''(4)''' | + | '''(4)''' Correct are the <u>solutions 1, 3 and 5</u>: |
| + | *The coded signal $q_{\rm C}(t)$ is binary $($level number $M = 2)$ with bit duration $T_{\rm B} = T_{\rm A}/8$. | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
| − | [[Category: | + | [[Category:Signal Representation: Exercises|^1.2 Signal Classification^]] |
Latest revision as of 09:42, 11 October 2021
All modern communication systems are digital. The principle of digital transmission of speech signals goes back to Alec Reeves, who invented the so-called "Puls Code Modulation" $\rm (PCM)$ as early as 1938.
On the right you see the (simplified) block diagram of the PCM transmitter with three functional units:
- The band-limited speech signal ${q(t)}$ is sampled, where the Sampling Theorem is observed, and yields the sampled signal $q_{\rm A}(t)$.
- Each sample $q_{\rm A}(t)$ is mapped to one of $M = 2^N$ results in the quantized signal $q_{\rm Q}(t)$.
- Each individual quantized value is represented by a code sequence of $N$ binary symbols and results in the coded signal $q_{\rm C}(t)$.
In this task only the different signals of the PCM transmitter are to be classified.
Later tasks will deal with other properties of the puls code modulation.
Note: This task belongs to the chapter Signal classification.
Questions
Solution
(1) Correct are the solutions 1, 2 and 4:
- The source signal ${q(t)}$ is analog, i.e. "continuous in time and value".
- In general, it makes no sense to transmit a deterministic signal.
- For the mathematical description, a deterministic source signal – such as a periodic signal – is better suited than a random signal.
- Deterministic signals are also used for testing in order to be able to reconstruct detected errors.
(2) Correct are the solution suggestions 2 and 3:
- After sampling, the signal $q_{\rm A}(t)$ is still continuous in value, but now also discrete in time.
- The sampling frequency $f_{\rm A}$ is given by the so-called "Sampling Theorem".
- The greater the maximum frequency $f_{\rm N,\,max}$ of the source signal, the greater must $f_{\rm A} ≥ 2 \cdot f_{\rm N,\,max}$ be selected.
(3) Correct are the solution suggestions 1 and 3:
- The quantized signal $q_{\rm Q}(t)$ is discrete in time and value, where the number of levels are $M = 2^8 = 256$ .
- A binary signal, on the other hand, is a discrete-valued signal with the level number $M = 2$.
(4) Correct are the solutions 1, 3 and 5:
- The coded signal $q_{\rm C}(t)$ is binary $($level number $M = 2)$ with bit duration $T_{\rm B} = T_{\rm A}/8$.