Difference between revisions of "Aufgaben:Exercise 1.2: Signal Classification"
From LNTwww
m (Guenter verschob die Seite 1.2 Signalklassifizierung nach Aufgabe 1.2: Signalklassifizierung) |
|||
| (29 intermediate revisions by 5 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Signal_Representation/Signal_classification}} |
| − | [[File:P_ID341_Sig_A_1_2.png|right| | + | [[File:P_ID341_Sig_A_1_2.png|right|frame|Preset signal waveforms]] |
| − | + | Three signal curves are shown on the right: | |
| − | * | + | *The blue signal <math>x_1(t)</math> is switched on at time $t = 0$ and has the value $1\,\text{V}\,$ for $t > 0$ . |
| − | * | + | *The red signal <math>x_2(t)\equiv 0</math> for $t < 0$ and jumps to $1\,\text{V}$ at $t = 0$ . It then decreases with the time constant $1\,\text{ms}$ . <br>For $t > 0$ the following applies: |
| − | :<math>x_2(t) = 1\,\text{V} \cdot {\rm e}^{- {t}/(1\,\text{ms})}.</math> | + | ::<math>x_2(t) = 1\,\text{V} \cdot {\rm e}^{- {t}/(1\,\text{ms})}.</math> |
| − | * | + | *Correspondingly, the following applies to the green signal <math>x_3(t)</math> for all $t$: |
| − | :<math>x_3(t) = 1\,\text{V} \cdot {\rm e}^{- {|t|}/(1\,\text{ms})}.</math> | + | ::<math>x_3(t) = 1\,\text{V} \cdot {\rm e}^{- {|\hspace{0.05cm}t\hspace{0.05cm}|}/(1\,\text{ms})}.</math> |
| − | + | You should now classify these three signals according to the following criteria: | |
| − | * | + | *deterministic or stochastic, |
| − | * | + | *causal or non–causal, |
| − | * | + | *energy-limited or power-limited, |
| − | * | + | *continuous-valued or discrete-valued, |
| − | * | + | *continuous in time or discrete in time. |
| − | |||
| − | |||
| − | |||
| − | === | + | |
| + | ''Note:'' | ||
| + | * This exercise belongs to the chapter [[Signal_Representation/Signal_classification|Signal Classification]]. | ||
| + | |||
| + | |||
| + | |||
| + | ===Questions=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Which of the following statements are true? |
|type="[]"} | |type="[]"} | ||
| − | + | + | + All signals considered here are deterministic. |
| − | - | + | - All signals considered here are of stochastic nature. |
| − | + | + | + The signals are always continuous in time. |
| − | - | + | - The signals are always continuous in value. |
| − | { | + | {Which signals are causal according to the definition in the theory part? |
|type="[]"} | |type="[]"} | ||
+ <math>x_1(t)</math>, | + <math>x_1(t)</math>, | ||
| Line 41: | Line 44: | ||
- <math>x_3(t)</math>. | - <math>x_3(t)</math>. | ||
| − | { | + | {Calculate the energy $E_2$ of the signal <math>x_2(t)</math> related to the unit resistance $R = 1\ Ω$. <br>What is the power <math>P_2</math> of this signal? |
|type="{}"} | |type="{}"} | ||
| − | <math>E_2 = </math>{ 0.5 5% } $ | + | <math>E_2 \ = \ </math>{ 0.5 5% } $\ \cdot 10^{-3}\,\text{V}^2\text{s}$ |
| − | <math>P_2 = </math>{ 0. } $ | + | <math>P_2 \ = \ </math>{ 0. } $\ \cdot \text{Vs}$ |
| − | { | + | {Which of the signals have a finite energy? |
|type="[]"} | |type="[]"} | ||
- <math>x_1(t)</math>, | - <math>x_1(t)</math>, | ||
| Line 55: | Line 58: | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''1 | + | '''(1)''' The <u>solutions 1 and 3</u> are applicable: |
| − | * | + | *All signals can be described completely in analytical form; therefore they are deterministic. |
| − | * | + | *All signals are also clearly defined for all times $t$ not only at certain times. Therefore, they are always continuous-time signals. |
| − | * | + | *The signal amplitudes of <math>x_2(t)</math> and <math>x_3(t)</math> can take any values between $0$ and $1\,\text{V}$ : they are <b>continuous in value</b>. |
| − | * | + | *On the other hand, with the signal <math>x_1(t)</math> only the two signal values $0$ and $1\,\text{V}$ are possible; this signal is <b>discrete in value</b>. |
| + | |||
| + | |||
| − | '''2 | + | '''(2)''' Correct are the <u>solutions 1 and 2</u>: |
| + | *A signal is called causal if for times $t < 0$ it does not exist or it is identically zero. This applies to the signals <math>x_1(t)</math> and <math>x_2(t)</math>. | ||
| + | *In contrast, <math>x_3(t)</math> belongs to the class of non-causal signals. | ||
| − | |||
| − | |||
| − | + | '''(3)''' According to the general definition: | |
| + | |||
| + | ::<math>E_2=\lim_{T_{\rm M}\to\infty}\int^{T_{\rm M}/2}_{-T_{\rm M}/2}x^2_2(t)\,\hspace{0.1cm}{\rm d}t.</math> | ||
| + | |||
| + | In this case, the lower integration limit is zero and the upper integration limit $+\infty$. You get: | ||
| − | <math>E_2=\int^\infty_0 (1{\rm V})^2\cdot{\rm e}^{-2t/(1\rm ms)}\,\hspace{0.1cm}{\rm d}t = 5 \cdot 10^{-4}\hspace{0.1cm} \rm V^2s \hspace{0.15cm}\underline{= 0.5 \cdot 10^{-3}\hspace{0.1cm} \rm V^2s}. </math> | + | ::<math>E_2=\int^\infty_0 (1{\rm V})^2\cdot{\rm e}^{-2t/(1\rm ms)}\,\hspace{0.1cm}{\rm d}t = 5 \cdot 10^{-4}\hspace{0.1cm} \rm V^2s \hspace{0.15cm}\underline{= 0.5 \cdot 10^{-3}\hspace{0.1cm} \rm V^2s}. </math> |
| + | |||
| + | With finite energy, the associated power is always negligible. From this follows $P_2\hspace{0.15cm}\underline{ = 0}$. | ||
| + | |||
| − | |||
| − | '''4 | + | '''(4)''' Correct are the <u>solutions 2 and 3</u>: |
| − | $E_2= 0.5 \cdot 10^{-3}\hspace{0.1cm} {\rm V^ | + | *As already calculated in the last subtask, <math>x_2(t)</math> has a finite energy: |
| + | :$$E_2= 0.5 \cdot 10^{-3}\hspace{0.1cm} {\rm V^2s}. $$ | ||
| − | + | *The energy of the signal <math>x_3(t)</math> is twice as large, since now the time domain $t < 0$ makes the same contribution as the time domain $t > 0$. So | |
| + | :$$E_3= 10^{-3}\hspace{0.1cm} {\rm V^2s}.$$ | ||
| − | + | *At signal <math>x_1(t)</math> the energy integral diverges: $E_1 \rightarrow \infty$. This signal has a finite power ⇒ $P_1= 0.5 \hspace{0.1cm} {\rm V}^2$. | |
| + | *The result also takes into account that the signal <math>x_1(t)</math> in half the time $(t < 0)$ is identical to zero. | ||
| + | * The signal <math>x_1(t)</math> therefore is <u>power–limited</u>. | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
__NOEDITSECTION__ | __NOEDITSECTION__ | ||
| − | [[Category: | + | [[Category:Signal Representation: Exercises|^1.2 Signal Classification^]] |
Latest revision as of 09:59, 11 October 2021
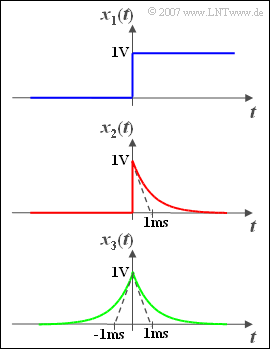
Three signal curves are shown on the right:
- The blue signal \(x_1(t)\) is switched on at time $t = 0$ and has the value $1\,\text{V}\,$ for $t > 0$ .
- The red signal \(x_2(t)\equiv 0\) for $t < 0$ and jumps to $1\,\text{V}$ at $t = 0$ . It then decreases with the time constant $1\,\text{ms}$ .
For $t > 0$ the following applies:
- \[x_2(t) = 1\,\text{V} \cdot {\rm e}^{- {t}/(1\,\text{ms})}.\]
- Correspondingly, the following applies to the green signal \(x_3(t)\) for all $t$:
- \[x_3(t) = 1\,\text{V} \cdot {\rm e}^{- {|\hspace{0.05cm}t\hspace{0.05cm}|}/(1\,\text{ms})}.\]
You should now classify these three signals according to the following criteria:
- deterministic or stochastic,
- causal or non–causal,
- energy-limited or power-limited,
- continuous-valued or discrete-valued,
- continuous in time or discrete in time.
Note:
- This exercise belongs to the chapter Signal Classification.
Questions
Solution
(1) The solutions 1 and 3 are applicable:
- All signals can be described completely in analytical form; therefore they are deterministic.
- All signals are also clearly defined for all times $t$ not only at certain times. Therefore, they are always continuous-time signals.
- The signal amplitudes of \(x_2(t)\) and \(x_3(t)\) can take any values between $0$ and $1\,\text{V}$ : they are continuous in value.
- On the other hand, with the signal \(x_1(t)\) only the two signal values $0$ and $1\,\text{V}$ are possible; this signal is discrete in value.
(2) Correct are the solutions 1 and 2:
- A signal is called causal if for times $t < 0$ it does not exist or it is identically zero. This applies to the signals \(x_1(t)\) and \(x_2(t)\).
- In contrast, \(x_3(t)\) belongs to the class of non-causal signals.
(3) According to the general definition:
- \[E_2=\lim_{T_{\rm M}\to\infty}\int^{T_{\rm M}/2}_{-T_{\rm M}/2}x^2_2(t)\,\hspace{0.1cm}{\rm d}t.\]
In this case, the lower integration limit is zero and the upper integration limit $+\infty$. You get:
- \[E_2=\int^\infty_0 (1{\rm V})^2\cdot{\rm e}^{-2t/(1\rm ms)}\,\hspace{0.1cm}{\rm d}t = 5 \cdot 10^{-4}\hspace{0.1cm} \rm V^2s \hspace{0.15cm}\underline{= 0.5 \cdot 10^{-3}\hspace{0.1cm} \rm V^2s}. \]
With finite energy, the associated power is always negligible. From this follows $P_2\hspace{0.15cm}\underline{ = 0}$.
(4) Correct are the solutions 2 and 3:
- As already calculated in the last subtask, \(x_2(t)\) has a finite energy:
- $$E_2= 0.5 \cdot 10^{-3}\hspace{0.1cm} {\rm V^2s}. $$
- The energy of the signal \(x_3(t)\) is twice as large, since now the time domain $t < 0$ makes the same contribution as the time domain $t > 0$. So
- $$E_3= 10^{-3}\hspace{0.1cm} {\rm V^2s}.$$
- At signal \(x_1(t)\) the energy integral diverges: $E_1 \rightarrow \infty$. This signal has a finite power ⇒ $P_1= 0.5 \hspace{0.1cm} {\rm V}^2$.
- The result also takes into account that the signal \(x_1(t)\) in half the time $(t < 0)$ is identical to zero.
- The signal \(x_1(t)\) therefore is power–limited.