Difference between revisions of "Aufgaben:Exercise 4.6: AWGN Channel Capacity"
| (27 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Information_Theory/AWGN_Channel_Capacity_for_Continuous_Input |
}} | }} | ||
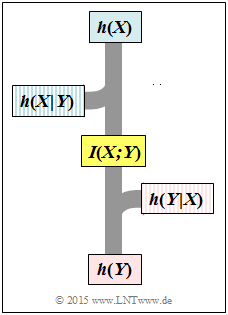
| − | [[File:P_ID2899__Inf_A_4_6.png|right|]] | + | [[File:P_ID2899__Inf_A_4_6.png|right|frame|Flowchart of the information]] |
| − | + | We start from the [[Information_Theory/AWGN–Kanalkapazität_bei_wertkontinuierlichem_Eingang#Channel_capacity_of_the_AWGN_channel| AWGN channel model]] : | |
| − | + | * $X$ denotes the input (transmitter). | |
| − | + | * $N$ stands for a Gaussian distributed noise. | |
| − | + | * $Y = X +N$ describes the output (receiver) in case of additive noise. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | : | + | For the probability density function $\rm (PDF)$ of the noise, let hold: |
| + | :$$f_N(n) = \frac{1}{\sqrt{2\pi \hspace{0.03cm}\sigma_{\hspace{-0.05cm}N}^2}} \cdot {\rm e}^{ | ||
| + | - \hspace{0.05cm}{n^2}\hspace{-0.05cm}/{(2 \hspace{0.03cm} \sigma_{\hspace{-0.05cm}N}^2) }} \hspace{0.05cm}.$$ | ||
| + | Since the random variable $N$ is zero mean ⇒ $m_{N} = 0$, we can equate the variance $\sigma_{\hspace{-0.05cm}N}^2$ with the power $P_N$ . In this case, the differential entropy of the random variable $N$ is specifiable (with the pseudo–unit "bit") as follows: | ||
| + | :$$h(N) = {1}/{2} \cdot {\rm log}_2\hspace{0.05cm}\left ( 2\pi {\rm e} \cdot P_N \right )\hspace{0.05cm}.$$ | ||
| + | In this exercise, $P_N = 1 \hspace{0.15cm} \rm mW$ is given. It should be noted: | ||
| − | + | * The power $P_N$ in the above equation, like the variance $\sigma_{\hspace{-0.05cm}N}^2$ , must be dimensionless. | |
| − | + | * To work with this equation, the physical quantity $P_N$ must be suitably normalized, for example corresponding to $P_N = 1 \hspace{0.15cm} \rm mW$ ⇒ $P_N\hspace{0.01cm}' = 1$. | |
| − | + | * With other normalization, for example $P_N = 1 \hspace{0.15cm} \rm mW$ ⇒ $P_N\hspace{0.01cm}' = 0.001$ a completely different numerical value would result fo $h(N)$ . | |
| − | :* | + | |
| − | $$C = \max_{\hspace{-0.15cm}f_X:\hspace{0.05cm} {\rm E}[X^2] \le P_X} \hspace{-0.2cm} I(X;Y) | + | Further, you can consider for the solution of this exercise: |
| + | |||
| + | * The channel capacity is defined as the maximum mutual information between input $X$ and output $Y$ with the best possible input distribution: | ||
| + | :$$C = \max_{\hspace{-0.15cm}f_X:\hspace{0.05cm} {\rm E}[X^2] \le P_X} \hspace{-0.2cm} I(X;Y) | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | + | *The channel capacity of the AWGN channel is: | |
| − | $$C_{\rm AWGN} = {1}/{2} \cdot {\rm log}_2\hspace{0.05cm}\left ( 1 + \frac{P_X}{P_N} \right ) | + | :$$C_{\rm AWGN} = {1}/{2} \cdot {\rm log}_2\hspace{0.05cm}\left ( 1 + \frac{P_X}{P_N} \right ) |
| − | = {1}/{2} \cdot {\rm log}_2\hspace{0.05cm}\left ( 1 + \frac{ | + | = {1}/{2} \cdot {\rm log}_2\hspace{0.05cm}\left ( 1 + \frac{P_{\hspace{-0.05cm}X}\hspace{0.01cm}'}{P_{\hspace{-0.05cm}N}\hspace{0.01cm}'} \right )\hspace{0.05cm}.$$ |
| − | + | :It can be seen: The channel capacity $C$ and also the mutual information $I(X; Y)$ are independent of the above normalization, in contrast to the differential entropies. | |
| + | |||
| + | * With Gaussian noise PDF $f_N(n)$, an Gaussian input PDF $f_X(x)$ leads to the maximum mutual information and thus to the channel capacity. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| − | |||
| − | |||
| − | === | + | Hints: |
| + | *The exercise belongs to the chapter [[Information_Theory/AWGN–Kanalkapazität_bei_wertkontinuierlichem_Eingang|AWGN channel capacity with continuous input]]. | ||
| + | *Since the results are to be given in "bit", "log" ⇒ "log<sub>2</sub>" is used in the equations. | ||
| + | |||
| + | |||
| + | |||
| + | ===Questions=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {What transmission power is required for $C = 2 \ \rm bit$? |
|type="{}"} | |type="{}"} | ||
| − | $ | + | $P_X \ = \ $ { 15 3% } $\ \rm mW$ |
| − | { | + | {Under which conditions is $I(X; Y) = 2 \ \rm bit$ achievable at all? |
|type="[]"} | |type="[]"} | ||
| − | + | + | + $P_X$ is determined as in '''(1)''' or larger. |
| − | + | + | + The random variable $X$ is Gaussian distributed. |
| − | + | + | + The random variable $X$ is zero mean. |
| − | + | + | + The random variables $X$ and $N$ are uncorrelated. |
| − | - | + | - The random variables $X$ and $Y$ are uncorrelated. |
| − | { | + | {Calculate the differential entropies of the random variables $N$, $X$ and $Y$ with appropriate normalization, <br>for example, $P_N = 1 \hspace{0.15cm} \rm mW$ ⇒ $P_N\hspace{0.01cm}' = 1$. |
|type="{}"} | |type="{}"} | ||
| − | $h(N)$ | + | $h(N) \ = \ $ { 2.047 3% } $\ \rm bit$ |
| − | $h(X)$ | + | $h(X) \ = \ $ { 4 3% } $\ \rm bit$ |
| − | $h(Y)$ | + | $h(Y) \ = \ $ { 4.047 3% } $\ \rm bit$ |
| − | { | + | {What are the other information-theoretic descriptive quantities? |
|type="{}"} | |type="{}"} | ||
| − | $h(Y|X)$ | + | $h(Y|X) \ = \ $ { 2.047 3% } $\ \rm bit$ |
| − | $h(X|Y)$ | + | $h(X|Y) \ = \ $ { 2 3% } $\ \rm bit$ |
| − | $h(XY)$ | + | $h(XY) \ = \ $ { 6.047 3% } $\ \rm bit$ |
| − | { | + | {What quantities would result for the same $P_X$ in the limiting case $P_N\hspace{0.01cm} ' \to 0$ ? |
|type="{}"} | |type="{}"} | ||
| − | $h(X)$ | + | $h(X) \ = \ $ { 4 3% } $\ \rm bit$ |
| − | $h(Y)$ | + | $h(Y|X) \ = \ $ { 0 3% } $\ \rm bit$ |
| − | $h(Y | + | $h(Y) \ = \ $ { 4 3% } $\ \rm bit$ |
| − | $ | + | $I(X;Y) \ = \ $ { 4 3% } $\ \rm bit$ |
| − | $ | + | $h(X|Y) \ = \ $ { 0. } $\ \rm bit$ |
| + | |||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | + | '''(1)''' The equation for the AWGN channel capacity in "bit" is: | |
| − | $$C_{\rm bit} = {1}/{2} \cdot {\rm log}_2\hspace{0.05cm}\left ( 1 + | + | :$$C_{\rm bit} = {1}/{2} \cdot {\rm log}_2\hspace{0.05cm}\left ( 1 + {P_X}/{P_N} \right )\hspace{0.05cm}.$$ |
| − | + | :With $C_{\rm bit} = 2$ this results in: | |
| − | $$4 \stackrel{!}{=} {\rm log}_2\hspace{0.05cm}\left ( 1 + | + | :$$4 \stackrel{!}{=} {\rm log}_2\hspace{0.05cm}\left ( 1 + {P_X}/{P_N} \right ) |
| − | \hspace{0.3cm}\Rightarrow \hspace{0.3cm} 1 + | + | \hspace{0.3cm}\Rightarrow \hspace{0.3cm} 1 + {P_X}/{P_N} \stackrel {!}{=} 2^4 = 16 |
\hspace{0.3cm}\Rightarrow \hspace{0.3cm} P_X = 15 \cdot P_N | \hspace{0.3cm}\Rightarrow \hspace{0.3cm} P_X = 15 \cdot P_N | ||
\hspace{0.15cm}\underline{= 15\,{\rm mW}} | \hspace{0.15cm}\underline{= 15\,{\rm mW}} | ||
\hspace{0.05cm}. $$ | \hspace{0.05cm}. $$ | ||
| − | + | ||
| − | + | ||
| − | + | '''(2)''' Correct are <u>proposed solutions 1 through 4</u>. Justification: | |
| − | + | * For $P_X < 15 \ \rm mW$ the mutual information $I(X; Y)$ will always be less than $2$ bit, regardless of all other conditions. | |
| − | + | * With $P_X = 15 \ \rm mW$ the maximum mutual information $I(X; Y) = 2$ bit is only achievable if the input quantity $X$ is Gaussian distributed. <br>The output quantity $Y$ is then also Gaussian distributed. | |
| − | + | * If the random variable $X$ has a constant proportion $m_X$ then the variance $\sigma_X^2 = P_X - m_X^2 $ for given $P_X$ is smaller, and it holds <br>$I(X; Y) = 1/2 · \log_2 \ (1 + \sigma_X^2/P_N) < 2$ bit. | |
| − | [[File: P_ID2901__Inf_A_4_6c.png |right|]] | + | * The precondition for the given channel capacity equation is that $X$ and $N$ are uncorrelated. On the other hand, if the random variables $X$ and $N$ were uncorrelated, then $I(X; Y) = 0$ would result. |
| − | + | ||
| − | $$h(N) \ = \ {1}/{2} \cdot {\rm log}_2\hspace{0.05cm}\left ( 2\pi {\rm e} \cdot 1 \right ) | + | |
| + | '''(3)''' The given equation for differential entropy makes sense only for dimensionless power. With the proposed normalization, one obtains: | ||
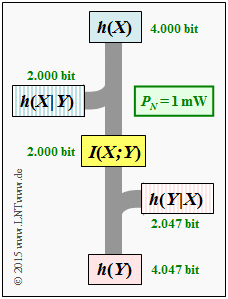
| + | [[File: P_ID2901__Inf_A_4_6c.png |right|frame|Information-theoretical values with the AWGN channel]] | ||
| + | * For $P_N = 1 \ \rm mW$ ⇒ $P_N\hspace{0.05cm}' = 1$: | ||
| + | :$$h(N) \ = \ {1}/{2} \cdot {\rm log}_2\hspace{0.05cm}\left ( 2\pi {\rm e} \cdot 1 \right ) | ||
= \ {1}/{2} \cdot {\rm log}_2\hspace{0.05cm}\left ( 17.08 \right ) | = \ {1}/{2} \cdot {\rm log}_2\hspace{0.05cm}\left ( 17.08 \right ) | ||
\hspace{0.15cm}\underline{= 2.047\,{\rm bit}}\hspace{0.05cm},$$ | \hspace{0.15cm}\underline{= 2.047\,{\rm bit}}\hspace{0.05cm},$$ | ||
| − | + | * For $P_X = 15 \ \rm mW$ ⇒ $P_X\hspace{0.01cm}' = 15$: | |
| − | $$h(X) \ = \ {1}/{2} \cdot {\rm log}_2\hspace{0.05cm}\left ( 2\pi {\rm e} \cdot 15 \right ) | + | :$$h(X) \ = \ {1}/{2} \cdot {\rm log}_2\hspace{0.05cm}\left ( 2\pi {\rm e} \cdot 15 \right ) = {1}/{2} \cdot {\rm log}_2\hspace{0.05cm}\left ( 2\pi {\rm e} \right ) + |
| − | + | {1}/{2} \cdot {\rm log}_2\hspace{0.05cm}\left (15 \right ) | |
| − | {1}/{2} \cdot {\rm log}_2\hspace{0.05cm}\left (15 \right ) | ||
| − | |||
\hspace{0.15cm}\underline{= 4.000\,{\rm bit}}\hspace{0.05cm}, $$ | \hspace{0.15cm}\underline{= 4.000\,{\rm bit}}\hspace{0.05cm}, $$ | ||
| − | + | * For $P_Y = P_X + P_N = 16 \ \rm mW$ ⇒ $P_Y\hspace{0.01cm}' = 16$: | |
| − | $$h(Y) = 2.047\,{\rm bit} + 2.000\,{\rm bit} | + | :$$h(Y) = 2.047\,{\rm bit} + 2.000\,{\rm bit} |
\hspace{0.15cm}\underline{= 4.047\,{\rm bit}}\hspace{0.05cm}.$$ | \hspace{0.15cm}\underline{= 4.047\,{\rm bit}}\hspace{0.05cm}.$$ | ||
| − | + | ||
| − | $$h(Y \hspace{-0.05cm}\mid \hspace{-0.05cm} X) = h(N) \hspace{0.15cm}\underline{= 2.047\,{\rm bit}}\hspace{0.05cm}.$$ | + | |
| − | + | ||
| − | $$h(Y \hspace{-0.05cm}\mid \hspace{-0.05cm} X) = h(Y) - I(X;Y) = 4.047 \,{\rm bit} - 2 \,{\rm bit} \hspace{0.15cm}\underline{= 2.047\,{\rm bit}}\hspace{0.05cm}. $$ | + | '''(4)''' The differential irrelevance for the AWGN channel: |
| − | + | :$$h(Y \hspace{-0.05cm}\mid \hspace{-0.05cm} X) = h(N) \hspace{0.15cm}\underline{= 2.047\,{\rm bit}}\hspace{0.05cm}.$$ | |
| − | $$h(X \hspace{-0.05cm}\mid \hspace{-0.05cm} Y) = h(X) - I(X;Y) = 4.000 \,{\rm bit} - 2 \,{\rm bit} \hspace{0.15cm}\underline{= 2.000\,{\rm bit}}\hspace{0.05cm}.$$ | + | *However, according to the adjacent graph, also holds: |
| − | + | :$$h(Y \hspace{-0.05cm}\mid \hspace{-0.05cm} X) = h(Y) - I(X;Y) = 4.047 \,{\rm bit} - 2 \,{\rm bit} \hspace{0.15cm}\underline{= 2.047\,{\rm bit}}\hspace{0.05cm}. $$ | |
| − | $$h(XY) = h(X) + h(Y) - I(X;Y) = 4.000 \,{\rm bit} + 4.047 \,{\rm bit} - 2 \,{\rm bit} \hspace{0.15cm}\underline{= 6.047\,{\rm bit}}\hspace{0.05cm}.$$ | + | *From this, the differential equivocation can be calculated as follows: |
| − | + | :$$h(X \hspace{-0.05cm}\mid \hspace{-0.05cm} Y) = h(X) - I(X;Y) = 4.000 \,{\rm bit} - 2 \,{\rm bit} \hspace{0.15cm}\underline{= 2.000\,{\rm bit}}\hspace{0.05cm}.$$ | |
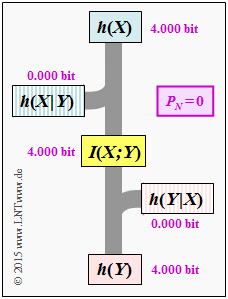
| − | + | [[File: P_ID2900__Inf_A_4_6e.png |right|frame|Information-theoretical values with the ideal channel]] | |
| − | $$h(Y \hspace{-0.05cm}\mid \hspace{-0.05cm} X) \ = \ h(N) \hspace{0.15cm}\underline{= 0\,{\rm (bit)}}\hspace{0.05cm},$$ $$ | + | *Finally, the differential composite entropy is also given, which cannot be read directly from the above diagram: |
| − | h(Y) \ = \ h(X) \hspace{0.15cm}\underline{= 4\,{\rm bit}}\hspace{0.05cm},$$ $$ | + | :$$h(XY) = h(X) + h(Y) - I(X;Y) = 4.000 \,{\rm bit} + 4.047 \,{\rm bit} - 2 \,{\rm bit} \hspace{0.15cm}\underline{= 6.047\,{\rm bit}}\hspace{0.05cm}.$$ |
| − | I(X;Y) \ = \ h(Y) - h(Y \hspace{-0.05cm}\mid \hspace{-0.05cm} X)\hspace{0.15cm}\underline{= 4\,{\rm bit}}\hspace{0.05cm},$$ $$ | + | |
| + | |||
| + | |||
| + | '''(5)''' For the ideal channel with $h(X)\hspace{0.15cm}\underline{= 4.000 \,{\rm bit}}$: | ||
| + | :$$h(Y \hspace{-0.05cm}\mid \hspace{-0.05cm} X) \ = \ h(N) \hspace{0.15cm}\underline{= 0\,{\rm (bit)}}\hspace{0.05cm},$$ | ||
| + | :$$h(Y) \ = \ h(X) \hspace{0.15cm}\underline{= 4\,{\rm bit}}\hspace{0.05cm},$$ | ||
| + | :$$I(X;Y) \ = \ h(Y) - h(Y \hspace{-0.05cm}\mid \hspace{-0.05cm} X)\hspace{0.15cm}\underline{= 4\,{\rm bit}}\hspace{0.05cm},$$ $$ | ||
h(X \hspace{-0.05cm}\mid \hspace{-0.05cm} Y) \ = \ h(X) - I(X;Y)\hspace{0.15cm}\underline{= 0\,{\rm (bit)}}\hspace{0.05cm}.$$ | h(X \hspace{-0.05cm}\mid \hspace{-0.05cm} Y) \ = \ h(X) - I(X;Y)\hspace{0.15cm}\underline{= 0\,{\rm (bit)}}\hspace{0.05cm}.$$ | ||
| − | |||
| − | + | *The graph shows these quantities in a flowchart. The same diagram would result in the discrete value case with $M = 16$ equally probable symbols ⇒ $H(X)= 4.000 \,{\rm bit}$. | |
| − | + | *One only would have to replace each $h$ by an $H$. | |
| − | |||
| − | |||
{{ML-Fuß}} | {{ML-Fuß}} | ||
| − | [[Category: | + | [[Category:Information Theory: Exercises|^4.2 AWGN and Value-Continuous Input^]] |
Latest revision as of 13:18, 3 November 2021
We start from the AWGN channel model :
- $X$ denotes the input (transmitter).
- $N$ stands for a Gaussian distributed noise.
- $Y = X +N$ describes the output (receiver) in case of additive noise.
For the probability density function $\rm (PDF)$ of the noise, let hold:
- $$f_N(n) = \frac{1}{\sqrt{2\pi \hspace{0.03cm}\sigma_{\hspace{-0.05cm}N}^2}} \cdot {\rm e}^{ - \hspace{0.05cm}{n^2}\hspace{-0.05cm}/{(2 \hspace{0.03cm} \sigma_{\hspace{-0.05cm}N}^2) }} \hspace{0.05cm}.$$
Since the random variable $N$ is zero mean ⇒ $m_{N} = 0$, we can equate the variance $\sigma_{\hspace{-0.05cm}N}^2$ with the power $P_N$ . In this case, the differential entropy of the random variable $N$ is specifiable (with the pseudo–unit "bit") as follows:
- $$h(N) = {1}/{2} \cdot {\rm log}_2\hspace{0.05cm}\left ( 2\pi {\rm e} \cdot P_N \right )\hspace{0.05cm}.$$
In this exercise, $P_N = 1 \hspace{0.15cm} \rm mW$ is given. It should be noted:
- The power $P_N$ in the above equation, like the variance $\sigma_{\hspace{-0.05cm}N}^2$ , must be dimensionless.
- To work with this equation, the physical quantity $P_N$ must be suitably normalized, for example corresponding to $P_N = 1 \hspace{0.15cm} \rm mW$ ⇒ $P_N\hspace{0.01cm}' = 1$.
- With other normalization, for example $P_N = 1 \hspace{0.15cm} \rm mW$ ⇒ $P_N\hspace{0.01cm}' = 0.001$ a completely different numerical value would result fo $h(N)$ .
Further, you can consider for the solution of this exercise:
- The channel capacity is defined as the maximum mutual information between input $X$ and output $Y$ with the best possible input distribution:
- $$C = \max_{\hspace{-0.15cm}f_X:\hspace{0.05cm} {\rm E}[X^2] \le P_X} \hspace{-0.2cm} I(X;Y) \hspace{0.05cm}.$$
- The channel capacity of the AWGN channel is:
- $$C_{\rm AWGN} = {1}/{2} \cdot {\rm log}_2\hspace{0.05cm}\left ( 1 + \frac{P_X}{P_N} \right ) = {1}/{2} \cdot {\rm log}_2\hspace{0.05cm}\left ( 1 + \frac{P_{\hspace{-0.05cm}X}\hspace{0.01cm}'}{P_{\hspace{-0.05cm}N}\hspace{0.01cm}'} \right )\hspace{0.05cm}.$$
- It can be seen: The channel capacity $C$ and also the mutual information $I(X; Y)$ are independent of the above normalization, in contrast to the differential entropies.
- With Gaussian noise PDF $f_N(n)$, an Gaussian input PDF $f_X(x)$ leads to the maximum mutual information and thus to the channel capacity.
Hints:
- The exercise belongs to the chapter AWGN channel capacity with continuous input.
- Since the results are to be given in "bit", "log" ⇒ "log2" is used in the equations.
Questions
Solution
- $$C_{\rm bit} = {1}/{2} \cdot {\rm log}_2\hspace{0.05cm}\left ( 1 + {P_X}/{P_N} \right )\hspace{0.05cm}.$$
- With $C_{\rm bit} = 2$ this results in:
- $$4 \stackrel{!}{=} {\rm log}_2\hspace{0.05cm}\left ( 1 + {P_X}/{P_N} \right ) \hspace{0.3cm}\Rightarrow \hspace{0.3cm} 1 + {P_X}/{P_N} \stackrel {!}{=} 2^4 = 16 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} P_X = 15 \cdot P_N \hspace{0.15cm}\underline{= 15\,{\rm mW}} \hspace{0.05cm}. $$
(2) Correct are proposed solutions 1 through 4. Justification:
- For $P_X < 15 \ \rm mW$ the mutual information $I(X; Y)$ will always be less than $2$ bit, regardless of all other conditions.
- With $P_X = 15 \ \rm mW$ the maximum mutual information $I(X; Y) = 2$ bit is only achievable if the input quantity $X$ is Gaussian distributed.
The output quantity $Y$ is then also Gaussian distributed. - If the random variable $X$ has a constant proportion $m_X$ then the variance $\sigma_X^2 = P_X - m_X^2 $ for given $P_X$ is smaller, and it holds
$I(X; Y) = 1/2 · \log_2 \ (1 + \sigma_X^2/P_N) < 2$ bit. - The precondition for the given channel capacity equation is that $X$ and $N$ are uncorrelated. On the other hand, if the random variables $X$ and $N$ were uncorrelated, then $I(X; Y) = 0$ would result.
(3) The given equation for differential entropy makes sense only for dimensionless power. With the proposed normalization, one obtains:
- For $P_N = 1 \ \rm mW$ ⇒ $P_N\hspace{0.05cm}' = 1$:
- $$h(N) \ = \ {1}/{2} \cdot {\rm log}_2\hspace{0.05cm}\left ( 2\pi {\rm e} \cdot 1 \right ) = \ {1}/{2} \cdot {\rm log}_2\hspace{0.05cm}\left ( 17.08 \right ) \hspace{0.15cm}\underline{= 2.047\,{\rm bit}}\hspace{0.05cm},$$
- For $P_X = 15 \ \rm mW$ ⇒ $P_X\hspace{0.01cm}' = 15$:
- $$h(X) \ = \ {1}/{2} \cdot {\rm log}_2\hspace{0.05cm}\left ( 2\pi {\rm e} \cdot 15 \right ) = {1}/{2} \cdot {\rm log}_2\hspace{0.05cm}\left ( 2\pi {\rm e} \right ) + {1}/{2} \cdot {\rm log}_2\hspace{0.05cm}\left (15 \right ) \hspace{0.15cm}\underline{= 4.000\,{\rm bit}}\hspace{0.05cm}, $$
- For $P_Y = P_X + P_N = 16 \ \rm mW$ ⇒ $P_Y\hspace{0.01cm}' = 16$:
- $$h(Y) = 2.047\,{\rm bit} + 2.000\,{\rm bit} \hspace{0.15cm}\underline{= 4.047\,{\rm bit}}\hspace{0.05cm}.$$
(4) The differential irrelevance for the AWGN channel:
- $$h(Y \hspace{-0.05cm}\mid \hspace{-0.05cm} X) = h(N) \hspace{0.15cm}\underline{= 2.047\,{\rm bit}}\hspace{0.05cm}.$$
- However, according to the adjacent graph, also holds:
- $$h(Y \hspace{-0.05cm}\mid \hspace{-0.05cm} X) = h(Y) - I(X;Y) = 4.047 \,{\rm bit} - 2 \,{\rm bit} \hspace{0.15cm}\underline{= 2.047\,{\rm bit}}\hspace{0.05cm}. $$
- From this, the differential equivocation can be calculated as follows:
- $$h(X \hspace{-0.05cm}\mid \hspace{-0.05cm} Y) = h(X) - I(X;Y) = 4.000 \,{\rm bit} - 2 \,{\rm bit} \hspace{0.15cm}\underline{= 2.000\,{\rm bit}}\hspace{0.05cm}.$$
- Finally, the differential composite entropy is also given, which cannot be read directly from the above diagram:
- $$h(XY) = h(X) + h(Y) - I(X;Y) = 4.000 \,{\rm bit} + 4.047 \,{\rm bit} - 2 \,{\rm bit} \hspace{0.15cm}\underline{= 6.047\,{\rm bit}}\hspace{0.05cm}.$$
(5) For the ideal channel with $h(X)\hspace{0.15cm}\underline{= 4.000 \,{\rm bit}}$:
- $$h(Y \hspace{-0.05cm}\mid \hspace{-0.05cm} X) \ = \ h(N) \hspace{0.15cm}\underline{= 0\,{\rm (bit)}}\hspace{0.05cm},$$
- $$h(Y) \ = \ h(X) \hspace{0.15cm}\underline{= 4\,{\rm bit}}\hspace{0.05cm},$$
- $$I(X;Y) \ = \ h(Y) - h(Y \hspace{-0.05cm}\mid \hspace{-0.05cm} X)\hspace{0.15cm}\underline{= 4\,{\rm bit}}\hspace{0.05cm},$$ $$ h(X \hspace{-0.05cm}\mid \hspace{-0.05cm} Y) \ = \ h(X) - I(X;Y)\hspace{0.15cm}\underline{= 0\,{\rm (bit)}}\hspace{0.05cm}.$$
- The graph shows these quantities in a flowchart. The same diagram would result in the discrete value case with $M = 16$ equally probable symbols ⇒ $H(X)= 4.000 \,{\rm bit}$.
- One only would have to replace each $h$ by an $H$.