Difference between revisions of "Aufgaben:Exercise 4.9: Higher-Level Modulation"
From LNTwww
| Line 5: | Line 5: | ||
[[File:EN_Inf_A_4_9.png|right|frame|Some channel capacity curves]] | [[File:EN_Inf_A_4_9.png|right|frame|Some channel capacity curves]] | ||
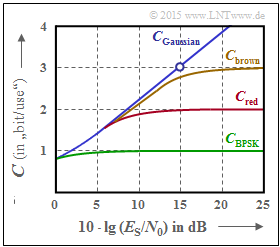
The graph shows AWGN channel capacity curves over the $10 \cdot \lg (E_{\rm S}/{N_0})$: | The graph shows AWGN channel capacity curves over the $10 \cdot \lg (E_{\rm S}/{N_0})$: | ||
| − | * $C_\text{ | + | * $C_\text{Gaussian}$: Shannon's boundary curve, |
| − | * $C_\text{BPSK}$: valid for | + | * $C_\text{BPSK}$: valid for "Binary Phase Shift Keying". |
| − | |||
| − | |||
| − | |||
| − | |||
| + | The two other curves $C_\text{red}$ and $C_\text{brown}$ should be analyzed and assigned to possible modulation schemes in subtasks '''(3)''' and '''(4)'''. | ||
| Line 19: | Line 16: | ||
Hints: | Hints: | ||
*The task belongs to the chapter [[Information_Theory/AWGN–Kanalkapazität_bei_wertdiskretem_Eingang|AWGN channel capacity with discrete value input]]. | *The task belongs to the chapter [[Information_Theory/AWGN–Kanalkapazität_bei_wertdiskretem_Eingang|AWGN channel capacity with discrete value input]]. | ||
| − | *Reference is made in particular to the page [[Information_Theory/AWGN–Kanalkapazität_bei_wertdiskretem_Eingang#The_channel_capacity_.7F.27.22.60UNIQ-MathJax81-QINU.60.22.27.7F_as_a_function_of_.7F.27.22.60UNIQ-MathJax82-QINU.60.22.27.7F| | + | *Reference is made in particular to the page [[Information_Theory/AWGN–Kanalkapazität_bei_wertdiskretem_Eingang#The_channel_capacity_.7F.27.22.60UNIQ-MathJax81-QINU.60.22.27.7F_as_a_function_of_.7F.27.22.60UNIQ-MathJax82-QINU.60.22.27.7F|Channel capacity $C$ as a function of $E_{\rm S}/{N_0}$]]. |
| − | *Since the results are to be given in "bit" | + | *Since the results are to be given in "bit" ⇒ "log" ⇒ "log<sub>2</sub>" is used in the equations. |
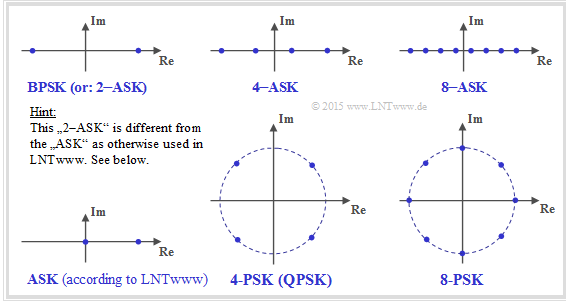
| − | *The modulation methods mentioned in the questions are described in terms of their signal space constellation | + | *The modulation methods mentioned in the questions are described in terms of their signal space constellation <br>(see lower graph). |
[[File:EN_Inf_A_4_9_Zusatz.png|right|frame|Proposed signal space constellations]] | [[File:EN_Inf_A_4_9_Zusatz.png|right|frame|Proposed signal space constellations]] | ||
| − | ''Notes on nomenclature:'' | + | '''Notes on nomenclature:''' |
| − | *In the literature,"BPSK" is sometimes also referred to as "2–ASK" | + | *In the literature, "BPSK" is sometimes also referred to as "2–ASK": |
:$$x ∈ X = \{+1,\ -1\}.$$ | :$$x ∈ X = \{+1,\ -1\}.$$ | ||
| − | *In contrast, in our learning tutorial | + | *In contrast, in our learning tutorial we understand as "ASK" the unipolar case: |
:$$x ∈ X = \{0,\ 1 \}.$$ | :$$x ∈ X = \{0,\ 1 \}.$$ | ||
*Therefore, according to our nomenclature: | *Therefore, according to our nomenclature: | ||
| − | :$$C_\text{ | + | :$$C_\text{ASK} < C_\text{BPSK}$$ |
| − | This fact is irrelevant for the solution of the present problem. | + | But: This fact is irrelevant for the solution of the present problem. |
| Line 40: | Line 37: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {What equation underlies | + | {What equation underlies Shannon's boundary curve $C_{\rm Gaussian}$? |
|type="[]"} | |type="[]"} | ||
| − | - $C_{\rm | + | - $C_{\rm Gaussian} = C_1= {1}/{2} \cdot {\rm log}_2 \hspace{0.1cm} ( 1 + E_{\rm S}/{N_0})$ , |
| − | + $C_{\rm | + | + $C_{\rm Gaussian} = C_2= {1}/{2} \cdot {\rm log}_2 \hspace{0.1cm} ( 1 + 2 \cdot E_{\rm S}/{N_0})$ , |
| − | - $C_{\rm | + | - $C_{\rm Gaussian} = C_3= {\rm log}_2 \hspace{0.1cm} ( 1 + E_{\rm S}/{N_0})$ . |
| − | {Which statements are true for the green curve $C_{\rm BPSK}$ | + | {Which statements are true for the green curve $(C_{\rm BPSK})$? |
|type="[]"} | |type="[]"} | ||
+ $C_{\rm BPSK}$ cannot be given in closed form. | + $C_{\rm BPSK}$ cannot be given in closed form. | ||
+ $C_{\rm BPSK}$ is greater than zero if $E_{\rm S}/{N_0} > 0$ is assumed. | + $C_{\rm BPSK}$ is greater than zero if $E_{\rm S}/{N_0} > 0$ is assumed. | ||
| − | - For $E_{\rm S}/{N_0} < \ln (2)$ | + | - For $E_{\rm S}/{N_0} < \ln (2)$ ⇒ $C_{\rm BPSK} ≡ 0$. |
| − | + In the whole range $C_{\rm BPSK} < C_{\rm | + | + In the whole range $C_{\rm BPSK} < C_{\rm Gaussian} $ is valid. |
| − | {Which statements are true for the red curve $C_{\rm red}$ | + | {Which statements are true for the red curve $(C_{\rm red})$? |
|type="[]"} | |type="[]"} | ||
| − | - For the associated random variable $X$ | + | - For the associated random variable $X$ holds $M_X = |X| = 2$. |
| − | + For the associated random variable $X$ | + | + For the associated random variable $X$ holds $M_X = |X| = 4$. |
| − | + $C_{\rm red}$ is simultaneously the channel capacity of the 4–ASK. | + | + $C_{\rm red}$ is simultaneously the channel capacity of the "4–ASK". |
| − | - $C_{\rm red}$ is simultaneously the channel capacity of the 4–QAM. | + | - $C_{\rm red}$ is simultaneously the channel capacity of the "4–QAM". |
+ For all $E_{\rm S}/{N_0} > 0$ $C_{\rm red}$ is between "green" and "brown". | + For all $E_{\rm S}/{N_0} > 0$ $C_{\rm red}$ is between "green" and "brown". | ||
| − | {Which statements are true for the brown curve $C_{\rm brown}$ | + | {Which statements are true for the brown curve $(C_{\rm brown})$? <br>Note: $p_{\rm B}$ denotes the bit error probability here. |
|type="[]"} | |type="[]"} | ||
| − | + For the associated random variable $X$ | + | + For the associated random variable $X$ ⇒ $M_X = |X| = 8$. |
| − | + $C_{\rm brown}$ is simultaneously the channel capacity of the 8–ASK. | + | + $C_{\rm brown}$ is simultaneously the channel capacity of the "8–ASK". |
| − | - $C_{\rm brown}$ is simultaneously the channel capacity of the 8–PSK. | + | - $C_{\rm brown}$ is simultaneously the channel capacity of the "8–PSK". |
| − | - $p_{\rm B} ≡ 0$ is possible with 8–ASK, $R = 2.5$ and $10 \cdot \lg (E_{\rm S}/{N_0}) = 10 \ \rm dB$ | + | - $p_{\rm B} ≡ 0$ is possible with "8–ASK", $R = 2.5$ and $10 \cdot \lg (E_{\rm S}/{N_0}) = 10 \ \rm dB$. |
| − | + $p_{\rm B} ≡ 0$ is possible with 8–ASK, $R = 2$ and $10 \cdot \lg (E_{\rm S}/{N_0}) = 10 \ \rm dB$ . | + | + $p_{\rm B} ≡ 0$ is possible with "8–ASK", $R = 2.0$ and $10 \cdot \lg (E_{\rm S}/{N_0}) = 10 \ \rm dB$ . |
Revision as of 15:03, 4 November 2021
The graph shows AWGN channel capacity curves over the $10 \cdot \lg (E_{\rm S}/{N_0})$:
- $C_\text{Gaussian}$: Shannon's boundary curve,
- $C_\text{BPSK}$: valid for "Binary Phase Shift Keying".
The two other curves $C_\text{red}$ and $C_\text{brown}$ should be analyzed and assigned to possible modulation schemes in subtasks (3) and (4).
Hints:
- The task belongs to the chapter AWGN channel capacity with discrete value input.
- Reference is made in particular to the page Channel capacity $C$ as a function of $E_{\rm S}/{N_0}$.
- Since the results are to be given in "bit" ⇒ "log" ⇒ "log2" is used in the equations.
- The modulation methods mentioned in the questions are described in terms of their signal space constellation
(see lower graph).
Notes on nomenclature:
- In the literature, "BPSK" is sometimes also referred to as "2–ASK":
- $$x ∈ X = \{+1,\ -1\}.$$
- In contrast, in our learning tutorial we understand as "ASK" the unipolar case:
- $$x ∈ X = \{0,\ 1 \}.$$
- Therefore, according to our nomenclature:
- $$C_\text{ASK} < C_\text{BPSK}$$
But: This fact is irrelevant for the solution of the present problem.
Questions
Solution
(1) Proposition 2 is correct, as shown by the calculation for $10 \cdot \lg (E_{\rm S}/{N_0}) = 15 \ \rm dB$ ⇒ $E_{\rm S}/{N_0} = 31.62$ zeigt:
- $$C_2(15\hspace{0.1cm}{\rm dB}) = {1}/{2} \cdot {\rm log}_2 \hspace{0.1cm} ( 1 + 2 \cdot 31.62 ) = {1}/{2} \cdot {\rm log}_2 \hspace{0.1cm} ( 64.25 ) \approx 3\,{\rm bit/Kanalzugriff}\hspace{0.05cm}. $$
- The other two proposed solutions provide the following numerical values:
- $$C_3(15\hspace{0.1cm}{\rm dB}) \ = \ {\rm log}_2 \hspace{0.1cm} ( 1 + 31.62 ) \approx 5.03\,{\rm bit/Kanalzugriff}\hspace{0.05cm},$$
- $$ C_1(15\hspace{0.1cm}{\rm dB}) \ = \ C_3/2 \approx 2.51\,{\rm bit/Kanalzugriff}\hspace{0.05cm}.$$
- The proposed solution 3 corresponds to the case of two independent Gaussian channels with half transmit power per channel.
(2) Proposed solutions 1, 2 and 4 are correct:
- If one would replace $E_{\rm S}$ by $E_{\rm B}$ , then also the statement 3 would be correct.
- For $E_{\rm B}/{N_0} < \ln (2)$ $C_{\rm Gauß} ≡ 0$ is valid and therefore also $C_{\rm BPSK} ≡ 0$ .
(3) Statements 2, 3 and 5 are correct::
- The red curve $C_{\rm red}$ is always above $C_{\rm BPSK}$ , but below $C_{\rm brown}$ and the Shannon boundary curve $C_{\rm Gauß}$.
- The statements also hold if for certain $E_{\rm S}/{N_0}$ values curves are indistinguishable within the character precision.
- From the limit $C_{\rm red}= 2 \ \rm bit/channel use$ for $E_{\rm S}/{N_0} → ∞$ , the symbol range $M_X = |X| = 4$.
- Thus, the red curve describes the 4–ASK. $M_X = |X| = 2$ would apply to the BPSK.
- The 4–QAM leads exactly to the same final value "2 bit/channel use". For small $E_{\rm S}/{N_0}$ values, however, the channel capacity $C_{\rm 4–QAM}$ is above the red curve, since $C_{\rm red}$ is bounded by the Gaussian boundary curve $C_2$ , but $C_{\rm 4–QAM}$ is bounded by $C_3$.
The designations $C_2$ and $C_3$ here refer to subtask (1).
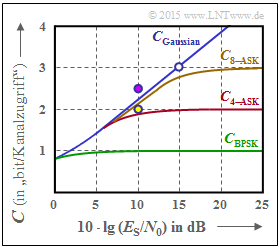
(4) Proposed solutions 1, 2 and 5 are correct:
- From the brown curve, one can see the correctness of the first two statements.
- The 8–PSK with I– and Q–components – i.e. with $K = 2$ dimensions – lies slightly above the brown curve for small $E_{\rm S}/{N_0}$ values ⇒ the answer 3 is incorrect.
In the graph, the two 8–ASK–systems are also drawn as dots according to propositions 4 and 5.
- The purple dot is above the $C_{\rm 8–ASK}$ curve ⇒ $R = 2.5$ and $10 \cdot \lg (E_{\rm S}/{N_0}) = 10 \ \rm dB$ are not enough to decode the 8–ASK without errors ⇒ $R > C$ ⇒ the channel coding theorem is not satisfied ⇒ answer 4 is wrong.
- However, if we reduce the code rate to $R = 2 < C_{\rm 8–ASK}$ according to the yellow dot for the same $10 \cdot \lg (E_{\rm S}/{N_0}) = 10 \ \rm dB$, the channel coding theorem is satisfied ⇒ Answer 5 is correct.