Difference between revisions of "Aufgaben:Exercise 4.1: Attenuation Function"
| (2 intermediate revisions by the same user not shown) | |||
| Line 3: | Line 3: | ||
}} | }} | ||
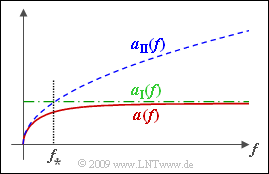
| − | [[File:P_ID1797__LZI_A_4_1.png|right|frame|Attenuation function and two bounds]] | + | [[File:P_ID1797__LZI_A_4_1.png|right|frame|Attenuation function per unit length ⇒ $\alpha(f)$ and two bounds]] |
The attenuation function per unit length ⇒ $\alpha(f)$ – pronounced "alpha" – of a line indicates the attenuation related to the line length. This quantity is determined by the primary line parameters $R\hspace{0.05cm}'$, $L\hspace{0.05cm}'$, $G\hspace{0.08cm}'$ and $C\hspace{0.08cm}'$ where the exact equation is somewhat complicated. Therefore, two more manageable approximations have been developed: | The attenuation function per unit length ⇒ $\alpha(f)$ – pronounced "alpha" – of a line indicates the attenuation related to the line length. This quantity is determined by the primary line parameters $R\hspace{0.05cm}'$, $L\hspace{0.05cm}'$, $G\hspace{0.08cm}'$ and $C\hspace{0.08cm}'$ where the exact equation is somewhat complicated. Therefore, two more manageable approximations have been developed: | ||
:$$\frac{\alpha_{_{\rm I}}(f)}{\rm Np} = {1}/{2} \cdot \left [R\hspace{0.05cm}' \cdot \sqrt{{C\hspace{0.08cm}'}/{ L\hspace{0.05cm}'} } + G\hspace{0.08cm}' \cdot \sqrt{{L\hspace{0.05cm}'}/{ C\hspace{0.08cm}'} }\hspace{0.05cm}\right ] | :$$\frac{\alpha_{_{\rm I}}(f)}{\rm Np} = {1}/{2} \cdot \left [R\hspace{0.05cm}' \cdot \sqrt{{C\hspace{0.08cm}'}/{ L\hspace{0.05cm}'} } + G\hspace{0.08cm}' \cdot \sqrt{{L\hspace{0.05cm}'}/{ C\hspace{0.08cm}'} }\hspace{0.05cm}\right ] | ||
| Line 33: | Line 33: | ||
| − | + | Notes: | |
*The exercise belongs to the chapter [[Linear_and_Time_Invariant_Systems/Some_Results_from_Line_Transmission_Theory|Some Results from Line Transmission Theory]]. | *The exercise belongs to the chapter [[Linear_and_Time_Invariant_Systems/Some_Results_from_Line_Transmission_Theory|Some Results from Line Transmission Theory]]. | ||
| Line 81: | Line 81: | ||
L' = 1.8\,\,{\rm mH}/{ {\rm km}} \hspace{0.05cm},\hspace{0.3cm} | L' = 1.8\,\,{\rm mH}/{ {\rm km}} \hspace{0.05cm},\hspace{0.3cm} | ||
G\hspace{0.03cm}' = 0.5\,\,{\rm µ S}/{ {\rm km}} \hspace{0.05cm},\hspace{0.3cm} | G\hspace{0.03cm}' = 0.5\,\,{\rm µ S}/{ {\rm km}} \hspace{0.05cm},\hspace{0.3cm} | ||
| − | C\hspace{0.03cm}' = 6.7\,\,{\rm nF}/{ {\rm km}} | + | C\hspace{0.03cm}' = 6.7\,\,{\rm nF}/{ {\rm km}}$: |
| − | |||
:$$\alpha_{\rm I}(f) = 1/2 \cdot | :$$\alpha_{\rm I}(f) = 1/2 \cdot | ||
\left [2.2 \cdot \sqrt{\frac{6.7 \cdot 10^{-9}}{ 1.8 \cdot 10^{-3}} } | \left [2.2 \cdot \sqrt{\frac{6.7 \cdot 10^{-9}}{ 1.8 \cdot 10^{-3}} } | ||
| Line 93: | Line 92: | ||
| − | + | '''(2)''' The bound $α_{\rm I}(f)$ calculated in subtask '''(1)''' is valid only for $f \gg f_∗$, while the bound $α_{\rm II}(f)$ is valid for $f \ll f_∗$. | |
| − | '''(2)''' The bound $α_{\rm I}(f)$ calculated in subtask '''(1)''' is valid only for $f \gg f_∗$, while the bound $α_{\rm II}(f)$ is valid for $f \ll f_∗$ | ||
*The characteristic frequency is obtained as the intersection of the two approximations: | *The characteristic frequency is obtained as the intersection of the two approximations: | ||
:$$\alpha_{\rm II}(f = f_{\star}) = \sqrt{1/2 \cdot \omega_{\star} \cdot R' \cdot C' }\hspace{0.1cm} | :$$\alpha_{\rm II}(f = f_{\star}) = \sqrt{1/2 \cdot \omega_{\star} \cdot R' \cdot C' }\hspace{0.1cm} | ||
\bigg |_{\omega_{\star} \hspace{0.05cm}= \hspace{0.05cm}2\pi f_{\star}} = \alpha_{\rm I}(f = f_{\star})$$ | \bigg |_{\omega_{\star} \hspace{0.05cm}= \hspace{0.05cm}2\pi f_{\star}} = \alpha_{\rm I}(f = f_{\star})$$ | ||
| − | *For the copper cable with $\text{0.6 mm}$ diameter, the following equation holds: | + | *For the copper cable with $\text{0.6 mm}$ diameter, the following equation holds: |
:$$f_{\star} = \frac {{\alpha^2_{_{\rm I}}(f = f_{\star})}}{\pi \cdot R' \cdot C'}= | :$$f_{\star} = \frac {{\alpha^2_{_{\rm I}}(f = f_{\star})}}{\pi \cdot R' \cdot C'}= | ||
\frac {0.496^2 \, {\rm 1/km^2}}{\pi \cdot 130\,{\rm \Omega/km} \cdot 35 \cdot 10^{-9}\,{\rm s/(\Omega \cdot km)}} | \frac {0.496^2 \, {\rm 1/km^2}}{\pi \cdot 130\,{\rm \Omega/km} \cdot 35 \cdot 10^{-9}\,{\rm s/(\Omega \cdot km)}} | ||
\hspace{0.15cm}\underline{= 17.2\,{\rm kHz}}\hspace{0.05cm}.$$ | \hspace{0.15cm}\underline{= 17.2\,{\rm kHz}}\hspace{0.05cm}.$$ | ||
| − | *In contrast, for the bronze line with diameter $\text{5 mm}$ : | + | *In contrast, for the bronze line with diameter $\text{5 mm}$ : |
:$$f_{\star} = | :$$f_{\star} = | ||
\frac {(2.25 \cdot 10^{-3})^2 }{\pi \cdot 2.2 \cdot 6.7 \cdot 10^{-9}}\,{\rm kHz} | \frac {(2.25 \cdot 10^{-3})^2 }{\pi \cdot 2.2 \cdot 6.7 \cdot 10^{-9}}\,{\rm kHz} | ||
\hspace{0.15cm}\underline{= 0.109\,{\rm kHz}}\hspace{0.05cm}.$$ | \hspace{0.15cm}\underline{= 0.109\,{\rm kHz}}\hspace{0.05cm}.$$ | ||
| − | |||
'''(3)''' For the copper cable $f_0 \ll f_∗$ holds. | '''(3)''' For the copper cable $f_0 \ll f_∗$ holds. | ||
| − | *Therefore, the approximation is $α_{\rm II}(f)$ ⇒ "strong attenuation" should be used: | + | *Therefore, the approximation is $α_{\rm II}(f)$ ⇒ "strong attenuation" should be used: |
:$$\alpha(f = f_0) \approx \sqrt{\pi \cdot f_0 \cdot R' \cdot C'}= \sqrt{\pi \cdot 2 \cdot 10^{3} \cdot 130 \cdot 35 \cdot 10^{-9}} | :$$\alpha(f = f_0) \approx \sqrt{\pi \cdot f_0 \cdot R' \cdot C'}= \sqrt{\pi \cdot 2 \cdot 10^{3} \cdot 130 \cdot 35 \cdot 10^{-9}} | ||
\hspace{0.1cm}{\rm Np}/{ {\rm km} } | \hspace{0.1cm}{\rm Np}/{ {\rm km} } | ||
\hspace{0.15cm}\underline{ = 0.17 \hspace{0.1cm}{\rm Np}/{ {\rm km} }} | \hspace{0.15cm}\underline{ = 0.17 \hspace{0.1cm}{\rm Np}/{ {\rm km} }} | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | *For the bronze line, because of $f_0 \gg f_∗$ the approximation is $α_{\rm I}(f)$ ⇒ "weak attenuation" is more suitable, see subtask '''(1)''': | + | *For the bronze line, because of $f_0 \gg f_∗$ the approximation is $α_{\rm I}(f)$ ⇒ "weak attenuation" is more suitable, see subtask '''(1)''': |
:$$\alpha(f = f_0) | :$$\alpha(f = f_0) | ||
\hspace{0.15cm}\underline{= 0.0023\hspace{0.1cm}{\rm Np}/{ {\rm km} }} | \hspace{0.15cm}\underline{= 0.0023\hspace{0.1cm}{\rm Np}/{ {\rm km} }} | ||
Latest revision as of 16:38, 6 November 2021
The attenuation function per unit length ⇒ $\alpha(f)$ – pronounced "alpha" – of a line indicates the attenuation related to the line length. This quantity is determined by the primary line parameters $R\hspace{0.05cm}'$, $L\hspace{0.05cm}'$, $G\hspace{0.08cm}'$ and $C\hspace{0.08cm}'$ where the exact equation is somewhat complicated. Therefore, two more manageable approximations have been developed:
- $$\frac{\alpha_{_{\rm I}}(f)}{\rm Np} = {1}/{2} \cdot \left [R\hspace{0.05cm}' \cdot \sqrt{{C\hspace{0.08cm}'}/{ L\hspace{0.05cm}'} } + G\hspace{0.08cm}' \cdot \sqrt{{L\hspace{0.05cm}'}/{ C\hspace{0.08cm}'} }\hspace{0.05cm}\right ] \hspace{0.05cm},$$
- $$\frac{\alpha_{_{\rm II}}(f)}{\rm Np} = \sqrt{1/2 \cdot \omega \cdot {R\hspace{0.05cm}' \cdot C\hspace{0.08cm}'} }\hspace{0.1cm} \bigg |_{\omega \hspace{0.05cm}= \hspace{0.05cm}2\pi f}\hspace{0.05cm}.$$
These two approximations are shown in the graph together with the actual $\alpha(f)$ curve. The intersection of $\alpha_{\rm I}(f)$ and $\alpha_{\rm II}(f)$ gives the characteristic frequency $f_∗$ with the following meaning:
- For $f \gg f_∗$ holds $α(f) ≈ α_{\rm I}(f)$.
- For $f \ll f_∗$ holds $α(f) ≈ α_{\rm II}(f)$.
These approximations are used to determine the function $\alpha(f)$ for a message signal of frequency $f_0 = 2 \ \rm kHz$, whereby the following transmission media are to be considered:
- a copper cable with $0.6 \ \rm mm$ diameter:
- $$R\hspace{0.05cm}' = 130\,\,{\rm \Omega}/{ {\rm km} }\hspace{0.05cm},\hspace{0.3cm} L\hspace{0.03cm}' = 0.6\,\,{\rm mH}/{ {\rm km}} \hspace{0.05cm},\hspace{0.3cm} G\hspace{0.08cm}' = 1\,\,{\rm µ S}/{ {\rm km}} \hspace{0.05cm},\hspace{0.3cm} C\hspace{0.08cm}' = 35\,\,{\rm nF}/{ {\rm km}} \hspace{0.05cm},$$
- a bronze overhead line with $5 \ \rm mm$ diameter:
- $$R\hspace{0.05cm}' = 2.2\,\,{\rm \Omega}/{ {\rm km} }\hspace{0.05cm},\hspace{0.3cm} L\hspace{0.03cm}' = 1.8\,\,{\rm mH}/{ {\rm km}} \hspace{0.05cm},\hspace{0.3cm} G\hspace{0.08cm}' = 0.5\,\,{\rm µ S}/{ {\rm km}} \hspace{0.05cm},\hspace{0.3cm} C\hspace{0.08cm}' = 6.7\,\,{\rm nF}/{ {\rm km}} \hspace{0.05cm}.$$
Notes:
- The exercise belongs to the chapter Some Results from Line Transmission Theory.
- The reference unit in the above equations for $α_{\rm I}(f)$ and $α_{\rm II}(f)$ and thus also for the total attenuation function (per unit length) $α(f)$ results from the fact that the magnitude frequency response is defined as $|H(f)| = {\rm e}^{-a}$ .
- From this follows for the attenuation $ a = - {\rm ln} \; |H(f)|$, where the relationship via the natural logarithm is denoted by "Neper" (Np).
- The unit of the attenuation function per unit length $α = a/l$ is thus "Np/km".
Questions
Solution
- $${\alpha_{_{\rm I}}(f)} = \frac{1 \,\rm Np/km}{2} \cdot \left [130\,{\rm \Omega} \cdot \sqrt{\frac{35 \cdot 10^{-9}\,{\rm s/\Omega}}{ 0.6 \cdot 10^{-3}\,{\rm \Omega \,s}} } + 10^{-6}\,{\rm \Omega^{-1}} \cdot \sqrt{\frac{0.6 \cdot 10^{-3}\,{\rm \Omega \,s}}{ 35 \cdot 10^{-9}\,{\rm s/\Omega}} }\hspace{0.1cm}\right ] $$
- $$ \Rightarrow \; \alpha_{\rm I}(f) = 1/2 \cdot \left [130 \cdot 7.638 \cdot 10^{-3}+ 10^{-6} \cdot 0.131 \cdot 10^{3}\right ] {\rm Np/km} \hspace{0.15cm}\underline{= 0.496\,{\rm Np/km}}\hspace{0.05cm}.$$
For the bronze line the result is $R\hspace{0.03cm}' = 2.2\,\,{\rm \Omega}/{ {\rm km} }\hspace{0.05cm},\hspace{0.3cm} L' = 1.8\,\,{\rm mH}/{ {\rm km}} \hspace{0.05cm},\hspace{0.3cm} G\hspace{0.03cm}' = 0.5\,\,{\rm µ S}/{ {\rm km}} \hspace{0.05cm},\hspace{0.3cm} C\hspace{0.03cm}' = 6.7\,\,{\rm nF}/{ {\rm km}}$:
- $$\alpha_{\rm I}(f) = 1/2 \cdot \left [2.2 \cdot \sqrt{\frac{6.7 \cdot 10^{-9}}{ 1.8 \cdot 10^{-3}} } + 0.5 \cdot 10^{-6} \cdot \sqrt{\frac{ 1.8 \cdot 10^{-3}} {6.7 \cdot 10^{-9}}}\hspace{0.1cm}\right ] $$
- $$ \Rightarrow \; \alpha_{\rm I}(f) = \frac{1 \,\rm Np/km}{2} \cdot \big [4.244 \cdot 10^{-3}+ 0.259 \cdot 10^{-3}\big ] {\rm Np/km} \hspace{0.15cm}\underline{= 0.0023\,{\rm Np}/{ {\rm km} }}\hspace{0.05cm}.$$
(2) The bound $α_{\rm I}(f)$ calculated in subtask (1) is valid only for $f \gg f_∗$, while the bound $α_{\rm II}(f)$ is valid for $f \ll f_∗$.
- The characteristic frequency is obtained as the intersection of the two approximations:
- $$\alpha_{\rm II}(f = f_{\star}) = \sqrt{1/2 \cdot \omega_{\star} \cdot R' \cdot C' }\hspace{0.1cm} \bigg |_{\omega_{\star} \hspace{0.05cm}= \hspace{0.05cm}2\pi f_{\star}} = \alpha_{\rm I}(f = f_{\star})$$
- For the copper cable with $\text{0.6 mm}$ diameter, the following equation holds:
- $$f_{\star} = \frac {{\alpha^2_{_{\rm I}}(f = f_{\star})}}{\pi \cdot R' \cdot C'}= \frac {0.496^2 \, {\rm 1/km^2}}{\pi \cdot 130\,{\rm \Omega/km} \cdot 35 \cdot 10^{-9}\,{\rm s/(\Omega \cdot km)}} \hspace{0.15cm}\underline{= 17.2\,{\rm kHz}}\hspace{0.05cm}.$$
- In contrast, for the bronze line with diameter $\text{5 mm}$ :
- $$f_{\star} = \frac {(2.25 \cdot 10^{-3})^2 }{\pi \cdot 2.2 \cdot 6.7 \cdot 10^{-9}}\,{\rm kHz} \hspace{0.15cm}\underline{= 0.109\,{\rm kHz}}\hspace{0.05cm}.$$
(3) For the copper cable $f_0 \ll f_∗$ holds.
- Therefore, the approximation is $α_{\rm II}(f)$ ⇒ "strong attenuation" should be used:
- $$\alpha(f = f_0) \approx \sqrt{\pi \cdot f_0 \cdot R' \cdot C'}= \sqrt{\pi \cdot 2 \cdot 10^{3} \cdot 130 \cdot 35 \cdot 10^{-9}} \hspace{0.1cm}{\rm Np}/{ {\rm km} } \hspace{0.15cm}\underline{ = 0.17 \hspace{0.1cm}{\rm Np}/{ {\rm km} }} \hspace{0.05cm}.$$
- For the bronze line, because of $f_0 \gg f_∗$ the approximation is $α_{\rm I}(f)$ ⇒ "weak attenuation" is more suitable, see subtask (1):
- $$\alpha(f = f_0) \hspace{0.15cm}\underline{= 0.0023\hspace{0.1cm}{\rm Np}/{ {\rm km} }} \hspace{0.05cm}.$$