Difference between revisions of "Aufgaben:Exercise 4.3: Operational Attenuation"
m (Guenter moved page Aufgabe 4.3: Betriebsdämpfung to Exercise 4.3: Effective Attenuation) |
|||
| (4 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Linear_and_Time_Invariant_Systems/Some_Results_from_Line_Transmission_Theory |
}} | }} | ||
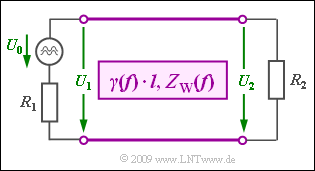
| − | [[File:P_ID1800__LZI_A_4_3.png|right|frame| | + | [[File:P_ID1800__LZI_A_4_3.png|right|frame|Considered line model]] |
| − | + | If a communication link of length $l$ is not terminated at both ends with its wave impedance $Z_{\rm W}$, reflections will always occur. | |
| − | + | Instead of the wave attenuation $a_{\rm W} = \alpha \cdot l$ one has to consider in this case the '''operating attenuation''' $a_{\rm B}$ (German: "Betriebsdämpfung" ⇒ subscipt "B"), which is given here without frequency dependence. That means: We always only consider a single frequency $f_0$: | |
| − | :$${ a}_{\rm B} = { a}_{\rm B}(f_0)= { a}_{\rm W}+ {\rm ln}\hspace{0.1cm} |q_1|+{\rm ln}\hspace{0.1cm} |q_2|+{ a}_{\rm | + | :$${ a}_{\rm B} = { a}_{\rm B}(f_0)= { a}_{\rm W}+ {\rm ln}\hspace{0.1cm} |q_1|+{\rm ln}\hspace{0.1cm} |q_2|+{ a}_{\rm IA}\hspace{0.05cm}.$$ |
| − | + | ||
| − | + | The four parts – all with the pseudo unit "Neper" (Np) – describe the following facts: | |
| − | * | + | * The first summand $a_{\rm W} = \alpha \cdot l$ models the '''wave attenuation''' of the wave propagating along the line. Note that attenuations are denoted by "$a$", while the attenuation function per unit length is denoted by "$\alpha$" ⇒ read: "alpha". |
| − | * | + | * The second summand gives the '''transmitter-side reflection loss'''. This term takes into account the power loss due to reflections at the "transmitter → line" transition: |
:$${\rm ln}\hspace{0.1cm} |q_1|= {\rm ln}\hspace{0.1cm}\frac {R_1 + Z_{\rm W}}{2 \cdot \sqrt{R_1 \cdot Z_{\rm W}}} | :$${\rm ln}\hspace{0.1cm} |q_1|= {\rm ln}\hspace{0.1cm}\frac {R_1 + Z_{\rm W}}{2 \cdot \sqrt{R_1 \cdot Z_{\rm W}}} | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | * In | + | * In an analogous way applies to the '''receiver-side reflection loss''' at the end of the line ⇒ transition "line → receiver": |
:$${\rm ln}\hspace{0.1cm} |q_2|= {\rm ln}\hspace{0.1cm}\frac {R_2 + Z_{\rm W}}{2 \cdot \sqrt{R_2 \cdot Z_{\rm W}}} | :$${\rm ln}\hspace{0.1cm} |q_2|= {\rm ln}\hspace{0.1cm}\frac {R_2 + Z_{\rm W}}{2 \cdot \sqrt{R_2 \cdot Z_{\rm W}}} | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | * | + | * The '''interaction attenuation (IA)''' describes the signal attenuation due to the effect of a doubly reflected wave, which can be constructively or destructively superimposed on the useful signal. For this last part holds: |
| − | :$${ a}_{\rm | + | :$${ a}_{\rm IA} = {\rm ln}\hspace{0.1cm} |1- r_1 \cdot r_2 \cdot {\rm e}^{- 2\hspace{0.05cm}\cdot\hspace{0.05cm} |
\gamma \hspace{0.05cm}\cdot\hspace{0.05cm} l}|$$ | \gamma \hspace{0.05cm}\cdot\hspace{0.05cm} l}|$$ | ||
| − | : | + | :we use the following equations and nomenclature in this exercise: |
| − | :$${a}_{\rm | + | :$${a}_{\rm IA} = {\rm ln}\hspace{0.1cm}A, \hspace{0.3cm}A = |1- r_\alpha \cdot {\rm e}^{-{\rm j}\hspace{0.05cm}\cdot\hspace{0.05cm} 2 \hspace{0.05cm}\cdot\hspace{0.05cm} |
\beta \hspace{0.05cm}\cdot\hspace{0.05cm} l}| | \beta \hspace{0.05cm}\cdot\hspace{0.05cm} l}| | ||
\hspace{0.05cm},\hspace{0.3cm}r_\alpha = r_1 \cdot r_2\cdot {\rm e}^{-2 \hspace{0.05cm}\cdot\hspace{0.05cm} | \hspace{0.05cm},\hspace{0.3cm}r_\alpha = r_1 \cdot r_2\cdot {\rm e}^{-2 \hspace{0.05cm}\cdot\hspace{0.05cm} | ||
| Line 34: | Line 34: | ||
| − | + | Notes: | |
| − | * | + | *The exercise belongs to the chapter [[Linear_and_Time_Invariant_Systems/Some_Results_from_Line_Transmission_Theory|Some Results from Line Transmission Theory]]. |
| − | * | + | *You can find essential information on the page [[Linear_and_Time_Invariant_Systems/Some_Results_from_Line_Transmission_Theory#Influence_of_reflections_-_operational_attenuation|Influence of reflections - operational attenuation]] |
| − | * | + | *Use the following numerical values for numerical calculations: |
:$$Z_{\rm W} = 100\,{\rm \Omega}\hspace{0.05cm},\hspace{0.3cm}R_1 = 200\,{\rm \Omega}\hspace{0.05cm},\hspace{0.3cm} | :$$Z_{\rm W} = 100\,{\rm \Omega}\hspace{0.05cm},\hspace{0.3cm}R_1 = 200\,{\rm \Omega}\hspace{0.05cm},\hspace{0.3cm} | ||
R_2 = 1\,{\rm k\Omega}\hspace{0.05cm},\hspace{0.3cm}l = 2\,{\rm km}\hspace{0.05cm},\hspace{0.3cm} | R_2 = 1\,{\rm k\Omega}\hspace{0.05cm},\hspace{0.3cm}l = 2\,{\rm km}\hspace{0.05cm},\hspace{0.3cm} | ||
| Line 44: | Line 44: | ||
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {What would be the value of the operating attenuation <u>with matching</u>, i.e. if there were no reflections? |
|type="{}"} | |type="{}"} | ||
$a_{\rm B} \ = \ $ { 0.2 3% } $\ \rm Np$ | $a_{\rm B} \ = \ $ { 0.2 3% } $\ \rm Np$ | ||
| − | { | + | {Calculate the two parts of the reflection loss for $Z_{\rm W} = 100\,{\rm \Omega}$ as well as $R_1 = 200\,{\rm \Omega}$ and $ R_2 = 1\,{\rm k\Omega}$. |
|type="{}"} | |type="{}"} | ||
$\ln\ |q_1| \ = \ $ { 0.059 3% } $\ \rm Np$ | $\ln\ |q_1| \ = \ $ { 0.059 3% } $\ \rm Np$ | ||
| Line 58: | Line 58: | ||
| − | { | + | {Calculate the reflection factors $r_1$, $r_2$ and $r_\alpha$. |
|type="{}"} | |type="{}"} | ||
$r_1 \ = \ $ { 0.333 3% } | $r_1 \ = \ $ { 0.333 3% } | ||
| Line 64: | Line 64: | ||
$r_\alpha\ = \ $ { 0.183 3% } | $r_\alpha\ = \ $ { 0.183 3% } | ||
| − | { | + | {Which condition must the auxiliary $A = \vert 1- r_\alpha \cdot {\rm e}^{-{\rm j}\hspace{0.05cm}\cdot\hspace{0.05cm} 2 \hspace{0.05cm}\cdot\hspace{0.05cm} \beta \hspace{0.05cm}\cdot\hspace{0.05cm} l}\vert $ satisfy, so that constructive or destructive superposition occurs with respect to the interaction attenuation? |
|type="[]"} | |type="[]"} | ||
| − | + $A$ | + | + $A$ is minimal ⇒ constructive superposition, |
| − | + $A$ | + | + $A$ is maximal ⇒ destructive superposition. |
| − | { | + | {Specify the smallest possible value $\beta_\text{min}$ for the phase function (per unit length) $\beta(f_0)$ , <br>so that constructive superposition occurs. |
|type="{}"} | |type="{}"} | ||
$\beta_\text{min} \ = \ $ { 0.785 3% } $\ \rm rad/km$ | $\beta_\text{min} \ = \ $ { 0.785 3% } $\ \rm rad/km$ | ||
| − | { | + | {What is the maximum size of the interaction attenuation component? What are the requirements for this? |
|type="{}"} | |type="{}"} | ||
| − | ${\rm Max}\ \big [a_\text{ | + | ${\rm Max}\ \big [a_\text{IA}\big ] \ = \ $ { 0.693 3% } $\ \rm Np$ |
| Line 83: | Line 83: | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' With resistance matching $(R_1 = R_2 =Z_{\rm W})$ only the first of the four summands remains: |
| − | :$${a}_{\rm B} = \alpha \cdot l = 0.1\,{\rm Np/km} \cdot 2\,{\rm km} \hspace{0.15cm}\underline{= 0.2\,{\rm Np}}\hspace{0.05cm}.$$ | + | :$${a}_{\rm B} = {a}_{\rm W} =\alpha \cdot l = 0.1\,{\rm Np/km} \cdot 2\,{\rm km} \hspace{0.15cm}\underline{= 0.2\,{\rm Np}}\hspace{0.05cm}.$$ |
| − | + | '''(2)''' According to the given equations we obtain: | |
| − | '''(2)''' | ||
:$$q_1 = \frac {R_1 + Z_{\rm W}}{2 \cdot \sqrt{R_1 \cdot Z_{\rm | :$$q_1 = \frac {R_1 + Z_{\rm W}}{2 \cdot \sqrt{R_1 \cdot Z_{\rm | ||
W}}}= \frac {200 + 100}{2 \cdot \sqrt{200 \cdot 100}}= 1.061 | W}}}= \frac {200 + 100}{2 \cdot \sqrt{200 \cdot 100}}= 1.061 | ||
| Line 101: | Line 100: | ||
| − | + | '''(3)''' With the given circuit resistors we obtain | |
| − | '''(3)''' | ||
:$$r_1= \frac {200\,{\rm \Omega} - 100\,{\rm \Omega}}{200\,{\rm \Omega} + 100\,{\rm \Omega}} \hspace{0.15cm}\underline{= 0.333}\hspace{0.05cm},$$ | :$$r_1= \frac {200\,{\rm \Omega} - 100\,{\rm \Omega}}{200\,{\rm \Omega} + 100\,{\rm \Omega}} \hspace{0.15cm}\underline{= 0.333}\hspace{0.05cm},$$ | ||
:$$r_2=\frac {1000\,{\rm \Omega} - 100\,{\rm \Omega}}{1000\,{\rm \Omega} + 100\,{\rm \Omega}}\hspace{0.15cm}\underline{ = | :$$r_2=\frac {1000\,{\rm \Omega} - 100\,{\rm \Omega}}{1000\,{\rm \Omega} + 100\,{\rm \Omega}}\hspace{0.15cm}\underline{ = | ||
| Line 112: | Line 110: | ||
| − | + | '''(4)''' <u>Both statements are correct</u>: | |
| − | '''(4)''' <u> | + | *With constructive superposition is ⇒ ${a}_{\rm IA} = {\rm ln}\hspace{0.1cm}A < 0 \; \Rightarrow \; A < 1$ and minimal. |
| − | * | + | *In contrast, the maximum value of $A $ (for which $A > 1$) causes positive interaction attenuation, i.e., additional attenuation of the useful signal due to destructive superposition of outgoing wave and returning wave. |
| − | * | ||
| − | |||
| − | '''(5)''' In | + | '''(5)''' In the last subtask, it was shown that constructive superposition is equivalent to the minimization of |
:$$A = |1- r_\alpha \cdot {\rm e}^{-{\rm j}\hspace{0.05cm}\cdot\hspace{0.05cm} 2\hspace{0.05cm}\cdot\hspace{0.05cm} | :$$A = |1- r_\alpha \cdot {\rm e}^{-{\rm j}\hspace{0.05cm}\cdot\hspace{0.05cm} 2\hspace{0.05cm}\cdot\hspace{0.05cm} | ||
\beta \hspace{0.05cm}\cdot\hspace{0.05cm} l}|= |1- r_\alpha \cdot \cos(2 \beta l)+ {\rm j} \cdot \sin(2 \beta | \beta \hspace{0.05cm}\cdot\hspace{0.05cm} l}|= |1- r_\alpha \cdot \cos(2 \beta l)+ {\rm j} \cdot \sin(2 \beta | ||
| Line 126: | Line 122: | ||
:$$ \Rightarrow \hspace{0.3cm }A = \sqrt {1+ {r_\alpha}^2- 2 \cdot r_\alpha \cdot \cos(2 \beta l)} | :$$ \Rightarrow \hspace{0.3cm }A = \sqrt {1+ {r_\alpha}^2- 2 \cdot r_\alpha \cdot \cos(2 \beta l)} | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | * | + | *The minimum results for |
:$$\cos(2 \beta l) = +1 \hspace{0.2cm}\Rightarrow \hspace{0.2cm}2 \beta | :$$\cos(2 \beta l) = +1 \hspace{0.2cm}\Rightarrow \hspace{0.2cm}2 \beta | ||
| − | l= \pi, 2\pi, 3\pi, ... \hspace{0.2cm}\Rightarrow | + | l= \pi,\ 2\pi,\ 3\pi, ... \hspace{0.2cm}\Rightarrow |
\hspace{0.2cm}\beta_{\rm min} = {\pi}({2l})\hspace{0.15cm}\underline{= 0.785\,{\rm rad/km}} | \hspace{0.2cm}\beta_{\rm min} = {\pi}({2l})\hspace{0.15cm}\underline{= 0.785\,{\rm rad/km}} | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | * | + | *In contrast, destructive superposition occurs if the phase function (per unit length) satisfies the following condition: |
:$$\cos(2 \beta l) = -1 \hspace{0.2cm}\Rightarrow \hspace{0.2cm}2 \beta | :$$\cos(2 \beta l) = -1 \hspace{0.2cm}\Rightarrow \hspace{0.2cm}2 \beta | ||
| − | l= {\pi}/{2}, {3\pi}/{2}, {5\pi}/{2},\text{ ...}$$ | + | l= {\pi}/{2},\ {3\pi}/{2},\ {5\pi}/{2},\text{ ...}$$ |
| − | '''(6)''' | + | '''(6)''' The argument $A = \sqrt {1+ {r_\alpha}^2- 2 \cdot r_\alpha \cdot \cos(2 \beta l)}$ can become maximum $A = 2$ ⇒ ${\rm Max}\ [a_\text{IA}] \; \underline {= 0.693 \ \rm Np}$. |
| − | + | The following requirements must be met for this: | |
| − | * | + | * not terminated line $(r_1 = r_2 = 1)$, |
| − | * | + | * short cable length, so the term $\alpha \cdot l$ is not effective $(r_\alpha = 1)$, |
| − | * | + | * phase progression according to the subtask '''(5)'''. |
{{ML-Fuß}} | {{ML-Fuß}} | ||
| − | [[Category:Linear and Time-Invariant Systems: Exercises|^4.1 | + | [[Category:Linear and Time-Invariant Systems: Exercises|^4.1 Results of Line Transmission Theory^]] |
Latest revision as of 16:02, 12 November 2021
If a communication link of length $l$ is not terminated at both ends with its wave impedance $Z_{\rm W}$, reflections will always occur.
Instead of the wave attenuation $a_{\rm W} = \alpha \cdot l$ one has to consider in this case the operating attenuation $a_{\rm B}$ (German: "Betriebsdämpfung" ⇒ subscipt "B"), which is given here without frequency dependence. That means: We always only consider a single frequency $f_0$:
- $${ a}_{\rm B} = { a}_{\rm B}(f_0)= { a}_{\rm W}+ {\rm ln}\hspace{0.1cm} |q_1|+{\rm ln}\hspace{0.1cm} |q_2|+{ a}_{\rm IA}\hspace{0.05cm}.$$
The four parts – all with the pseudo unit "Neper" (Np) – describe the following facts:
- The first summand $a_{\rm W} = \alpha \cdot l$ models the wave attenuation of the wave propagating along the line. Note that attenuations are denoted by "$a$", while the attenuation function per unit length is denoted by "$\alpha$" ⇒ read: "alpha".
- The second summand gives the transmitter-side reflection loss. This term takes into account the power loss due to reflections at the "transmitter → line" transition:
- $${\rm ln}\hspace{0.1cm} |q_1|= {\rm ln}\hspace{0.1cm}\frac {R_1 + Z_{\rm W}}{2 \cdot \sqrt{R_1 \cdot Z_{\rm W}}} \hspace{0.05cm}.$$
- In an analogous way applies to the receiver-side reflection loss at the end of the line ⇒ transition "line → receiver":
- $${\rm ln}\hspace{0.1cm} |q_2|= {\rm ln}\hspace{0.1cm}\frac {R_2 + Z_{\rm W}}{2 \cdot \sqrt{R_2 \cdot Z_{\rm W}}} \hspace{0.05cm}.$$
- The interaction attenuation (IA) describes the signal attenuation due to the effect of a doubly reflected wave, which can be constructively or destructively superimposed on the useful signal. For this last part holds:
- $${ a}_{\rm IA} = {\rm ln}\hspace{0.1cm} |1- r_1 \cdot r_2 \cdot {\rm e}^{- 2\hspace{0.05cm}\cdot\hspace{0.05cm} \gamma \hspace{0.05cm}\cdot\hspace{0.05cm} l}|$$
- we use the following equations and nomenclature in this exercise:
- $${a}_{\rm IA} = {\rm ln}\hspace{0.1cm}A, \hspace{0.3cm}A = |1- r_\alpha \cdot {\rm e}^{-{\rm j}\hspace{0.05cm}\cdot\hspace{0.05cm} 2 \hspace{0.05cm}\cdot\hspace{0.05cm} \beta \hspace{0.05cm}\cdot\hspace{0.05cm} l}| \hspace{0.05cm},\hspace{0.3cm}r_\alpha = r_1 \cdot r_2\cdot {\rm e}^{-2 \hspace{0.05cm}\cdot\hspace{0.05cm} \alpha \hspace{0.05cm}\cdot\hspace{0.05cm} l},\hspace{0.3cm}r_1= \frac {R_1 - Z_{\rm W}}{R_1 + Z_{\rm W}}, \hspace{0.3cm}r_2= \frac {R_2 - Z_{\rm W}}{R_2 + Z_{\rm W}} \hspace{0.05cm}.$$
Notes:
- The exercise belongs to the chapter Some Results from Line Transmission Theory.
- You can find essential information on the page Influence of reflections - operational attenuation
- Use the following numerical values for numerical calculations:
- $$Z_{\rm W} = 100\,{\rm \Omega}\hspace{0.05cm},\hspace{0.3cm}R_1 = 200\,{\rm \Omega}\hspace{0.05cm},\hspace{0.3cm} R_2 = 1\,{\rm k\Omega}\hspace{0.05cm},\hspace{0.3cm}l = 2\,{\rm km}\hspace{0.05cm},\hspace{0.3cm} \alpha = 0.1\,{\rm Np/km} \hspace{0.05cm}.$$
Questions
Solution
- $${a}_{\rm B} = {a}_{\rm W} =\alpha \cdot l = 0.1\,{\rm Np/km} \cdot 2\,{\rm km} \hspace{0.15cm}\underline{= 0.2\,{\rm Np}}\hspace{0.05cm}.$$
(2) According to the given equations we obtain:
- $$q_1 = \frac {R_1 + Z_{\rm W}}{2 \cdot \sqrt{R_1 \cdot Z_{\rm W}}}= \frac {200 + 100}{2 \cdot \sqrt{200 \cdot 100}}= 1.061 \hspace{0.2cm}\Rightarrow \hspace{0.2cm} {\rm ln}\hspace{0.1cm}|q_1| \hspace{0.15cm}\underline{= 0.059 \,{\rm Np}} \hspace{0.05cm},$$
- $$q_2 = \frac {R_2 + Z_{\rm W}}{2 \cdot \sqrt{R_2 \cdot Z_{\rm W}}}= \frac {1000 + 100}{2 \cdot \sqrt{1000 \cdot 100}}= 1.739 \hspace{0.2cm}\Rightarrow \hspace{0.2cm} {\rm ln}\hspace{0.1cm}|q_2| \hspace{0.15cm}\underline{= 0.553 \,{\rm Np}}\hspace{0.05cm}.$$
(3) With the given circuit resistors we obtain
- $$r_1= \frac {200\,{\rm \Omega} - 100\,{\rm \Omega}}{200\,{\rm \Omega} + 100\,{\rm \Omega}} \hspace{0.15cm}\underline{= 0.333}\hspace{0.05cm},$$
- $$r_2=\frac {1000\,{\rm \Omega} - 100\,{\rm \Omega}}{1000\,{\rm \Omega} + 100\,{\rm \Omega}}\hspace{0.15cm}\underline{ = 0.818}$$
- $$\Rightarrow \hspace{0.3cm} r_\alpha = r_1 \cdot r_2\cdot {\rm e}^{-2 \hspace{0.05cm}\cdot\hspace{0.05cm} \alpha \hspace{0.05cm}\cdot\hspace{0.05cm} l}= 0.333 \cdot 0.818\cdot {\rm e}^{-4}\hspace{0.15cm}\underline{= 0.183} \hspace{0.05cm}.$$
(4) Both statements are correct:
- With constructive superposition is ⇒ ${a}_{\rm IA} = {\rm ln}\hspace{0.1cm}A < 0 \; \Rightarrow \; A < 1$ and minimal.
- In contrast, the maximum value of $A $ (for which $A > 1$) causes positive interaction attenuation, i.e., additional attenuation of the useful signal due to destructive superposition of outgoing wave and returning wave.
(5) In the last subtask, it was shown that constructive superposition is equivalent to the minimization of
- $$A = |1- r_\alpha \cdot {\rm e}^{-{\rm j}\hspace{0.05cm}\cdot\hspace{0.05cm} 2\hspace{0.05cm}\cdot\hspace{0.05cm} \beta \hspace{0.05cm}\cdot\hspace{0.05cm} l}|= |1- r_\alpha \cdot \cos(2 \beta l)+ {\rm j} \cdot \sin(2 \beta l)| = \sqrt {1- 2 \cdot r_\alpha \cdot \cos(2 \beta l)+ {r_\alpha}^2 \cdot \cos^2(2 \beta l)+ {r_\alpha}^2 \cdot \sin^2(2 \beta l)}$$
- $$ \Rightarrow \hspace{0.3cm }A = \sqrt {1+ {r_\alpha}^2- 2 \cdot r_\alpha \cdot \cos(2 \beta l)} \hspace{0.05cm}.$$
- The minimum results for
- $$\cos(2 \beta l) = +1 \hspace{0.2cm}\Rightarrow \hspace{0.2cm}2 \beta l= \pi,\ 2\pi,\ 3\pi, ... \hspace{0.2cm}\Rightarrow \hspace{0.2cm}\beta_{\rm min} = {\pi}({2l})\hspace{0.15cm}\underline{= 0.785\,{\rm rad/km}} \hspace{0.05cm}.$$
- In contrast, destructive superposition occurs if the phase function (per unit length) satisfies the following condition:
- $$\cos(2 \beta l) = -1 \hspace{0.2cm}\Rightarrow \hspace{0.2cm}2 \beta l= {\pi}/{2},\ {3\pi}/{2},\ {5\pi}/{2},\text{ ...}$$
(6) The argument $A = \sqrt {1+ {r_\alpha}^2- 2 \cdot r_\alpha \cdot \cos(2 \beta l)}$ can become maximum $A = 2$ ⇒ ${\rm Max}\ [a_\text{IA}] \; \underline {= 0.693 \ \rm Np}$.
The following requirements must be met for this:
- not terminated line $(r_1 = r_2 = 1)$,
- short cable length, so the term $\alpha \cdot l$ is not effective $(r_\alpha = 1)$,
- phase progression according to the subtask (5).