Difference between revisions of "Aufgaben:Exercise 1.1: A Special Dice Game"
| (16 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Theory_of_Stochastic_Signals/Some_Basic_Definitions}} |
| − | |||
| − | |||
| − | |||
| − | + | [[File:P_ID3__Sto_A1_1.jpg|right|frame|About the dice game "Max"]] | |
| − | + | In the dice game "Max" two dice are thrown. The higher number of points of the two dice is multiplied by $10$ and then the lower number of points is added to it. For example, a "2" and a "4" gives the game result $42$ and a "5" and a "6" gives the result $65$. The smallest possible result of a roll is therefore $31$. The following rules also apply: | |
| − | |||
| + | *A "double" (the same number twice) is generally valued higher than two unequal dice. | ||
| + | *Thus, a "double one" is higher than $65$, but lower than any other double. | ||
| + | *A special position in this game is occupied by the "Max" (a "1" and a "2"). This combination, shown in the picture, is higher than the "double six". | ||
| − | |||
| + | Player $X$ starts the game. He wins if the player $Y$ cannot beat the presented result. The other multiple options of this game are not considered here. | ||
| Line 17: | Line 16: | ||
| − | + | Hints: | |
| − | * | + | *The exercise belongs to the chapter [[Theory_of_Stochastic_Signals/Some_Basic_Definitions | Some basic definitions of probability theory]]. |
| − | * | + | *The sample solution is summarized in a short (German language) [[Würfelspiel_„Mäxchen”_(Lernvideo)|learning video]]. |
| − | + | ===Questions=== | |
| − | === | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Do $X$ and $Y$ have equal chances of winning? If you think the game is unfair: How could the game be made fair? |
|type="[]"} | |type="[]"} | ||
| − | - | + | - Players $X$ and $Y$ have equal chances. |
| − | + | + | + Player $X$ has an advantage. |
| − | - | + | - Player $Y$ has an advantage. |
| − | { | + | {How many different outcomes $(I)$ are possible in this game? |
|type="{}"} | |type="{}"} | ||
$I \ =\ $ { 21 } | $I \ =\ $ { 21 } | ||
| − | { | + | {What is the probability of a "double six"? |
|type="{}"} | |type="{}"} | ||
| − | $\rm Pr\big[ | + | $\rm Pr\big[\text{"double six"}\big]\ =\ $ { 0.0278 3% } |
| − | { | + | {What is the probability of rolling "any double"? |
|type="{}"} | |type="{}"} | ||
| − | $\rm Pr\big[ | + | $\rm Pr\big[\text{"any double"}\big]\ =\ $ { 0.1667 3% } |
| − | { | + | {What is the probability that a player rolls a "Max"? |
|type="{}"} | |type="{}"} | ||
| − | $\rm Pr\big[ | + | $\rm Pr\big[\text{"Max"}\big]\ =\ $ { 0.0556 3% } |
| − | { | + | {Player $X$ has rolled a "3" and a "5". Under this assumption, what is player $Y$'s chance of winning?? |
|type="{}"} | |type="{}"} | ||
| − | ${\rm Pr}\big[Y\; {\rm | + | ${\rm Pr}\big[Y\; {\rm wins}\big]\ =\ $ { 0.5556 3% } |
| − | { | + | {What is the minimum score $R_{\rm \min}$ that player $X$ must achieve to have a greater chance of winning than $75\%$? |
|type="{}"} | |type="{}"} | ||
$R_{\rm \min}\ =\ $ { 65 } | $R_{\rm \min}\ =\ $ { 65 } | ||
| Line 58: | Line 56: | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' <u> | + | '''(1)''' <u>Player $X$ has an advantage</u>, because player $Y$ has to trump him. |
| + | *The game would be fair, for example, if it were scored as a "draw" when the rolls were exactly equal. | ||
| + | *However, over a longer period of time, even if $X$ and $Y$ start alternating, there will be equal chances of winning. | ||
| − | |||
| + | '''(2)''' $\underline{I = 21}$ different outcomes are possible. These are (starting with the lowest): | ||
| + | :$$31, 32, 41, 42, 43, 51, 52, 53, 54, 61, 62, 63, 64, 65, 11, 22, 33, 44, 55, 66, 21.$$ | ||
| − | |||
| + | '''(3)''' However, the $21$ possible results of this dice game are not equally probable, therefore the probabilities cannot be determined according to the classical definition $($the result would be $1/21)$. | ||
| − | + | *If one at least mentally makes a distinction between the dice, for example by a blue $(B)$ and a red $(R)$ one there are $6^{2} = 36$ equally probable events, among others the event ${\rm Pr\big[\text{"double six"}\big]} = Pr\big[(B = 6) \cap (R = 6)\big]$. | |
| + | *For both dice, the probability of a "6" is equal to $1/6$. Since the numbers of the two dice are, of course, statistically independent, the following is true: | ||
| − | :$$ | + | :$$Pr\big[\text{"double six"}\big] = {\rm Pr}(B = 6 \cap R = 6) = 1/36 \;\underline{= 0.0278}.$$ |
| + | |||
| + | "Note": From the naming "result", one might incorrectly conclude that this is an outcome. However, according to the definitions in this chapter, the result is to be considered as an event (summary of outcomes). | ||
| + | |||
| − | + | [[File:EN_Sto_A1_1_g.png|right|400px|Sum of two dice]] | |
| + | '''(4)''' This probability can be stated with $K = 6$ and $M = 36$ as follows: | ||
| + | :$${\rm Pr\big[\text{"any double"}\big] = Pr}(B = R) = K/M = 1/6 \; \underline{= 0.1667}.$$ | ||
| − | |||
| − | + | '''(5)''' Analogously, the probability for the "Max" can be calculated with $K = 2$ and $M = 36$: | |
| + | :$${\rm Pr\big[\text{"Max"}\big] = Pr}(B = 1 \cap R = 2) + {\rm Pr}(B = 2 \cap R = 1) = 1/18 \; \underline{= 0.0556}.$$ | ||
| − | |||
| − | + | '''(6)''' The probability that $Y$ wins if $X$ got "53" is $5/9\; \underline{\approx 0.555}$. | |
| + | The sample solution of this subtask is summarized in a short (German language) [[Würfelspiel_„Mäxchen”_(Lernvideo)|learning video]]. | ||
| − | |||
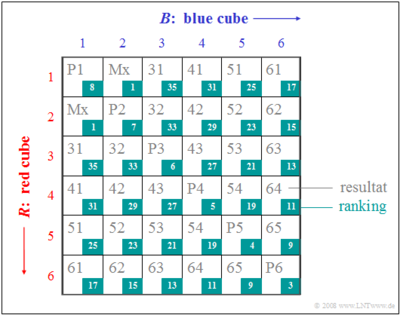
| − | + | '''(7)''' To solve the last sub-task, we again assume a two-dimensional representation and rank the matrix elements according to their values (see graph). From this we can see: | |
| − | '''(7)''' | + | *With the default value of $65$, the opponent has only a chance of winning of $8/36 = 0.222$. |
| − | * | + | *This means that your own chance of winning is about $77.8\%$. |
| − | * | + | *With $64$, on the other hand, player $X$'s chance of winning would be only about $72.2\%$. |
| − | * | + | *The correct solution is therefore $R_\min\; \underline{ = 65}$. |
{{ML-Fuß}} | {{ML-Fuß}} | ||
| − | [[Category: | + | [[Category:Theory of Stochastic Signals: Exercises|^1.1 Some Basic Definitions^]] |
Latest revision as of 17:47, 18 November 2021
In the dice game "Max" two dice are thrown. The higher number of points of the two dice is multiplied by $10$ and then the lower number of points is added to it. For example, a "2" and a "4" gives the game result $42$ and a "5" and a "6" gives the result $65$. The smallest possible result of a roll is therefore $31$. The following rules also apply:
- A "double" (the same number twice) is generally valued higher than two unequal dice.
- Thus, a "double one" is higher than $65$, but lower than any other double.
- A special position in this game is occupied by the "Max" (a "1" and a "2"). This combination, shown in the picture, is higher than the "double six".
Player $X$ starts the game. He wins if the player $Y$ cannot beat the presented result. The other multiple options of this game are not considered here.
Hints:
- The exercise belongs to the chapter Some basic definitions of probability theory.
- The sample solution is summarized in a short (German language) learning video.
Questions
Solution
- The game would be fair, for example, if it were scored as a "draw" when the rolls were exactly equal.
- However, over a longer period of time, even if $X$ and $Y$ start alternating, there will be equal chances of winning.
(2) $\underline{I = 21}$ different outcomes are possible. These are (starting with the lowest):
- $$31, 32, 41, 42, 43, 51, 52, 53, 54, 61, 62, 63, 64, 65, 11, 22, 33, 44, 55, 66, 21.$$
(3) However, the $21$ possible results of this dice game are not equally probable, therefore the probabilities cannot be determined according to the classical definition $($the result would be $1/21)$.
- If one at least mentally makes a distinction between the dice, for example by a blue $(B)$ and a red $(R)$ one there are $6^{2} = 36$ equally probable events, among others the event ${\rm Pr\big[\text{"double six"}\big]} = Pr\big[(B = 6) \cap (R = 6)\big]$.
- For both dice, the probability of a "6" is equal to $1/6$. Since the numbers of the two dice are, of course, statistically independent, the following is true:
- $$Pr\big[\text{"double six"}\big] = {\rm Pr}(B = 6 \cap R = 6) = 1/36 \;\underline{= 0.0278}.$$
"Note": From the naming "result", one might incorrectly conclude that this is an outcome. However, according to the definitions in this chapter, the result is to be considered as an event (summary of outcomes).
(4) This probability can be stated with $K = 6$ and $M = 36$ as follows:
- $${\rm Pr\big[\text{"any double"}\big] = Pr}(B = R) = K/M = 1/6 \; \underline{= 0.1667}.$$
(5) Analogously, the probability for the "Max" can be calculated with $K = 2$ and $M = 36$:
- $${\rm Pr\big[\text{"Max"}\big] = Pr}(B = 1 \cap R = 2) + {\rm Pr}(B = 2 \cap R = 1) = 1/18 \; \underline{= 0.0556}.$$
(6) The probability that $Y$ wins if $X$ got "53" is $5/9\; \underline{\approx 0.555}$.
The sample solution of this subtask is summarized in a short (German language) learning video.
(7) To solve the last sub-task, we again assume a two-dimensional representation and rank the matrix elements according to their values (see graph). From this we can see:
- With the default value of $65$, the opponent has only a chance of winning of $8/36 = 0.222$.
- This means that your own chance of winning is about $77.8\%$.
- With $64$, on the other hand, player $X$'s chance of winning would be only about $72.2\%$.
- The correct solution is therefore $R_\min\; \underline{ = 65}$.