Difference between revisions of "Aufgaben:Exercise 1.2Z: Sets of Digits"
From LNTwww
| (25 intermediate revisions by 5 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Theory_of_Stochastic_Signals/Set_Theory_Basics}} |
| − | [[File: | + | [[File:EN_Sto_Z_1_2_neu.png|right|frame|Sets of digits: $A$, $B$, $C$]] |
| − | + | Let the universal set $G$ be the set of all digits between $1$ and $9$. Given are the following subsets: | |
| − | $$A = [\text{ | + | :$$A = \big[\text{digits} \leqslant 3\big],$$ |
| − | $$ B = [\text{ | + | :$$ B = \big[\text{digits divisible by 3}\big],$$ |
| − | $$ C = [\text{ | + | :$$ C = \big[\text{digits 5, 6, 7, 8}\big].$$ |
| − | + | Besides these, let other sets be defined: | |
| − | $$D = (A \cap \ | + | :$$D = (A \cap \overline B) \cup (\overline A \cap B),$$ |
| − | $$E = (A \cup B) \cap (\ | + | :$$E = (A \cup B) \cap (\overline A \cup \overline B), $$ |
| − | $$F = (A \cup C) \cap \ | + | :$$F = (A \cup C) \cap \overline B, $$ |
| − | $$ | + | :$$H = (\overline A \cap \overline C) \cup (A \cap B \cap C).$$ |
| − | + | ||
| − | + | First consider which digits belong to the sets $D$, $E$, $F$ and $H$ and then answer the following questions. <br>Justify your answers in terms of set theory. | |
| − | === | + | |
| + | |||
| + | |||
| + | |||
| + | Hints: | ||
| + | *The task belongs to the chapter [[Theory_of_Stochastic_Signals/Set_Theory_Basics|Set Theory Basics]]. | ||
| + | |||
| + | *The topic of this chapter is illustrated with examples in the (German language) learning video | ||
| + | |||
| + | :[[Mengentheoretische_Begriffe_und_Gesetzmäßigkeiten_(Lernvideo)|Mengentheoretische Begriffe und Gesetzmäßigkeiten]] $\Rightarrow$ "Set Theoretical Concepts and Laws". | ||
| + | |||
| + | |||
| + | ===Questions=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Which of the following statements are correct? |
|type="[]"} | |type="[]"} | ||
| − | - $A$ | + | - $A$ and $B$ are disjoint sets. |
| − | + $A$ | + | + $A$ and $C$ are disjoint sets. |
| − | - $B$ | + | - $B$ and $C$ are disjoint sets. |
| − | { | + | {Which of the following statements are correct? |
|type="[]"} | |type="[]"} | ||
| − | - | + | - The union $A \cup B \cup C$ gives the universal set $G$. |
| − | + | + | + The complementary set to $A \cap B \cap C$ gives the universal set $G$. |
| − | { | + | {Which of the following statements are correct? |
|type="[]"} | |type="[]"} | ||
| − | + | + | + The complementary sets of $D$ and $E$ are identical. |
| − | + $F$ | + | + $F$ is a subset of the complementary set of $B$. |
| − | - | + | - The sets $B$, $C$ and $D$ form a complete system. |
| − | + | + | + The sets $A$, $C$ and $H$ form a complete system. |
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | : | + | For the other sets defined in the problem holds: |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | $ | + | :$$ D = (A \cap \overline B) \cup (\overline A \cap B) |
| − | + | =\big[\{1, 2, 3\} \cap \{1, 2, 4, 5, 7, 8\}\big] \cup \big[\{4, 5, 6, 7, 8, 9\} \cap \{3, 6, 9\}\big] = \{1, 2, 6, 9\},$$ | |
| − | ( | + | :$$ E = (A \cup B) \cap (\overline A \cup \overline B) = (A \cap \overline A) \cup (A \cap \overline B) \cup (\overline A \cap B) \cup (\overline A \cap \overline B) = (A \cap \overline B) \cup (\overline A \cap B) = D = \{1, 2, 6, 9\},$$ |
| − | ( | + | :$$F = (A \cup C) \cap \overline B = \{1, 2, 3, 5, 6, 7, 8\} \cap \{1, 2, 4, 5, 7, 8\} = \{1, 2, 5, 7, 8\},$$ |
| − | |||
| − | + | :$$H = (\bar A \cap \overline C) \cup (A \cap B \cap C) = (\overline A \cap \overline C) \cup \phi = \{4, 9\}.$$ | |
| − | + | '''(1)''' Only the <u>proposed solution 2</u> is correct: | |
| + | * $A$ and $C$ have no common element. | ||
| + | * $A$ and $B$ each contain a $3$. | ||
| + | * $B$ and $C$ each contain a $6$. | ||
| − | |||
| − | |||
| − | |||
| − | $ | + | '''(2)''' Correct is the <u>proposed solution 2</u>: |
| + | *No digit is contained in $A$, $B$ and $C$ at the same time ⇒ $ A \cap B \cap C = \phi$ ⇒ $ \overline{A \cap B \cap C} = \overline{\phi} = G$. | ||
| + | *The first proposition, on the other hand, is wrong. It is missing a $4$. | ||
| − | |||
| − | |||
| − | $A = \{1, 2, 3\},$ | + | '''(3)''' Correct are the <u>proposed solutions 1, 2 and 4</u>: |
| + | *The first proposal is correct: The sets $D$ and $E$ contain exactly the same elements and thus also their complementary sets. | ||
| + | *The second proposal is also correct: In general, i.e. for any $X$ and $B$ the following holds: $(X \cap \overline B) \subset \overline B \ \Rightarrow$ With $X = A \cup C$ it follows that $F \subset \overline B$. | ||
| + | *The last proposal is also correct: $A = \{1, 2, 3\},$ $C = \{5, 6, 7, 8\}$ and $H = \{4, 9\}$ form a "complete system". | ||
| + | *The third suggestion, on the other hand, is wrong because $B$ and $C$ are not disjoint. | ||
| − | |||
{{ML-Fuß}} | {{ML-Fuß}} | ||
| − | [[Category: | + | [[Category:Theory of Stochastic Signals: Exercises|^1.2 Set Theory Basics |
^]] | ^]] | ||
Latest revision as of 14:13, 25 November 2021
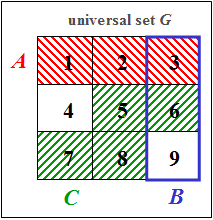
Let the universal set $G$ be the set of all digits between $1$ and $9$. Given are the following subsets:
- $$A = \big[\text{digits} \leqslant 3\big],$$
- $$ B = \big[\text{digits divisible by 3}\big],$$
- $$ C = \big[\text{digits 5, 6, 7, 8}\big].$$
Besides these, let other sets be defined:
- $$D = (A \cap \overline B) \cup (\overline A \cap B),$$
- $$E = (A \cup B) \cap (\overline A \cup \overline B), $$
- $$F = (A \cup C) \cap \overline B, $$
- $$H = (\overline A \cap \overline C) \cup (A \cap B \cap C).$$
First consider which digits belong to the sets $D$, $E$, $F$ and $H$ and then answer the following questions.
Justify your answers in terms of set theory.
Hints:
- The task belongs to the chapter Set Theory Basics.
- The topic of this chapter is illustrated with examples in the (German language) learning video
- Mengentheoretische Begriffe und Gesetzmäßigkeiten $\Rightarrow$ "Set Theoretical Concepts and Laws".
Questions
Solution
For the other sets defined in the problem holds:
- $$ D = (A \cap \overline B) \cup (\overline A \cap B) =\big[\{1, 2, 3\} \cap \{1, 2, 4, 5, 7, 8\}\big] \cup \big[\{4, 5, 6, 7, 8, 9\} \cap \{3, 6, 9\}\big] = \{1, 2, 6, 9\},$$
- $$ E = (A \cup B) \cap (\overline A \cup \overline B) = (A \cap \overline A) \cup (A \cap \overline B) \cup (\overline A \cap B) \cup (\overline A \cap \overline B) = (A \cap \overline B) \cup (\overline A \cap B) = D = \{1, 2, 6, 9\},$$
- $$F = (A \cup C) \cap \overline B = \{1, 2, 3, 5, 6, 7, 8\} \cap \{1, 2, 4, 5, 7, 8\} = \{1, 2, 5, 7, 8\},$$
- $$H = (\bar A \cap \overline C) \cup (A \cap B \cap C) = (\overline A \cap \overline C) \cup \phi = \{4, 9\}.$$
(1) Only the proposed solution 2 is correct:
- $A$ and $C$ have no common element.
- $A$ and $B$ each contain a $3$.
- $B$ and $C$ each contain a $6$.
(2) Correct is the proposed solution 2:
- No digit is contained in $A$, $B$ and $C$ at the same time ⇒ $ A \cap B \cap C = \phi$ ⇒ $ \overline{A \cap B \cap C} = \overline{\phi} = G$.
- The first proposition, on the other hand, is wrong. It is missing a $4$.
(3) Correct are the proposed solutions 1, 2 and 4:
- The first proposal is correct: The sets $D$ and $E$ contain exactly the same elements and thus also their complementary sets.
- The second proposal is also correct: In general, i.e. for any $X$ and $B$ the following holds: $(X \cap \overline B) \subset \overline B \ \Rightarrow$ With $X = A \cup C$ it follows that $F \subset \overline B$.
- The last proposal is also correct: $A = \{1, 2, 3\},$ $C = \{5, 6, 7, 8\}$ and $H = \{4, 9\}$ form a "complete system".
- The third suggestion, on the other hand, is wrong because $B$ and $C$ are not disjoint.