Difference between revisions of "Aufgaben:Exercise 1.3Z: Winning with Roulette?"
m (Text replacement - "”" to """) |
|||
| (7 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Theory_of_Stochastic_Signals/Set_Theory_Basics}} |
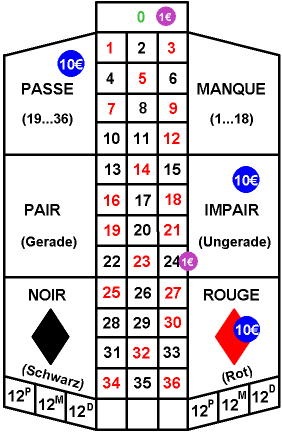
| − | [[File:P_ID82__Sto_Z_1_3.gif|right|frame| | + | [[File:P_ID82__Sto_Z_1_3.gif|right|frame|Considered betting situation]] |
| − | + | In roulette, a winning number $Z$ is determined in each game by means of a ball and a roulette wheel, where we want to assume that all possible numbers $Z \in \{0, 1, 2, \ \text{...} \ , 36 \}$ are equally probable. | |
| − | + | The players can now bet on a single number or on a group of numbers with chips of different value. Some of the possibilities and the corresponding winnings will be briefly explained here on the basis of the chips bet by a player (see graph): | |
| − | * | + | *If a player bets on a number (in the example on "0"), he would get back $35$ times his stake as winnings in addition to his bet. |
| − | * | + | *If a player bets on a group of numbers with three fields (in the example, the 1-euro chip for the numbers from "22" to "24"), he would receive $ 11$ times his stake as winnings in addition to his bet. |
| − | * | + | *If a player bets on a group of numbers with $ 18$ fields (for example, the 10-euro chips on "Rouge", on "Impair" and on "Passe"), he will receive the same amount back as winnings in addition to his bet. |
| − | * | + | *If the number drawn does not belong to one of the squares he occupies, his bet is lost. |
| + | Hints: | ||
| + | *The exercise belongs to the chapter [[Theory_of_Stochastic_Signals/Set_Theory_Basics|Set Theory Basics]]. | ||
| + | *'''Enter any losses as negative winnings''' in the following questions. | ||
| + | *The topic of this chapter is illustrated with examples in the (German language) learning video | ||
| + | :[[Mengentheoretische_Begriffe_und_Gesetzmäßigkeiten_(Lernvideo)|Mengentheoretische Begriffe und Gesetzmäßigkeiten]] $\Rightarrow$ "Set-Theoretical Concepts and Laws". | ||
| − | + | ===Questions=== | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | === | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {A player simultaneously places one 1-euro chip on each of the squares "0", "Red" and "Black". What are his average winnings per game? |
|type="{}"} | |type="{}"} | ||
| − | $G_1 \ =\ $ { -0.083--0.079 } $\ \rm | + | $G_1 \ =\ $ { -0.083--0.079 } $\ \rm euro$ |
| − | { | + | {How much does he win on average per game if he always places one $1$ Euro chip on each of the squares "Red" and "Black"? |
|type="{}"} | |type="{}"} | ||
| − | $G_2 \ =\ $ { -0.056--0.052 } $\ \rm | + | $G_2 \ =\ $ { -0.056--0.052 } $\ \rm euro$ |
| − | { | + | {How much does he win on average per game if he always bets $1$ Euro on "0" and $10$ Euro on "Red"? |
|type="{}"} | |type="{}"} | ||
| − | $G_3 \ =\ $ { -0.307--0.287 } $\ \rm | + | $G_3 \ =\ $ { -0.307--0.287 } $\ \rm euro$ |
| − | { | + | {The player bets as shown in the picture. Which number $Z_{\rm desire}$ should he be hoping for? How big would his winnings be then? |
|type="{}"} | |type="{}"} | ||
| − | $Z_{\rm | + | $Z_{\rm desire} \ = \ $ { 23 } |
| − | $G_4 \ =\ $ { 40 3% } $\ \rm | + | $G_4 \ =\ $ { 40 3% } $\ \rm euro$ |
| − | { | + | {Is there a betting combination such that the average winnings are positive? |
|type="()"} | |type="()"} | ||
| − | - | + | - Yes ⇒ Quit university and go to the next casino. |
| − | + | + | + No ⇒ Continue with $\rm LNTwww$. |
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' The player loses one euro each time if one of the numbers $1$ to $36$ is drawn. |
| − | * | + | *He wins $33$ euro, if $0$ is drawn. It follows that: |
| − | :$$G_1 =\rm {36}/{37}\cdot (-1\hspace{0.1cm} | + | :$$G_1 =\rm {36}/{37}\cdot (-1\hspace{0.1cm} euro) + {1}/{37}\cdot (33\hspace{0.1cm} euro) \hspace{0.15cm}\underline {= - 0.081\hspace{0.1cm} euro\hspace{0.1cm}(Loss)}.$$ |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | '''(2)''' The player wins and loses nothing unless the zero is drawn. If the zero appears, he loses his bet: | ||
| + | :$$G_2 = \rm {1}/{37}\cdot (-2\hspace{0.1cm} euro)\hspace{0.15cm}\underline { = -0.054 \hspace{0.1cm}euro \hspace{0.1cm}(Loss)}.$$ | ||
| − | |||
| − | |||
| − | |||
| − | |||
| + | '''(3)''' If "red" is drawn, he wins nine euro. | ||
| + | *If "zero" comes, he effectively wins $25$ euro. | ||
| + | *If "black" is drawn, he loses his entire bet of $11$ euro: | ||
| + | :$$G_3 = \rm {18}/{37}\cdot (10 -1) + {1}/{37}\cdot (35-10) + {18}/{37}\cdot (-10-1)\hspace{0.15cm}\underline { = - 0.297\hspace{0.1cm}euro}.$$ | ||
| − | '''(4)''' | + | '''(4)''' He gets the highest winning at $Z_{\rm desire} \; \underline{ = 23} $. Then four of his five chips win: |
| − | :$$G_4 = \rm 10\hspace{0.1cm}( | + | :$$G_4 = \rm 10\hspace{0.1cm}(Red) + 10\hspace{0.1cm}(Passe) + 10\hspace{0.1cm}(Impair) + |
| − | \rm 11\hspace{0.1cm}( | + | \rm 11\hspace{0.1cm}(between \hspace{0.1cm}22\hspace{0.1cm} and \hspace{0.1cm}24) - 1 \hspace{0.1cm}(not \hspace{0.1cm}0) \hspace{0.15cm}\underline {= 40 \hspace{0.1cm}euro}.$$ |
| − | * | + | *If, on the other hand, the "zero" comes, he wins only $\rm 35 - 31 = 4 \ euro$. |
| − | '''(5)''' | + | '''(5)''' '''No, unfortunately not. On statistical average, the house always wins'''. |
{{ML-Fuß}} | {{ML-Fuß}} | ||
| − | [[Category:Theory of Stochastic Signals: Exercises|^1.2 | + | [[Category:Theory of Stochastic Signals: Exercises|^1.2 Set Theory Basics |
^]] | ^]] | ||
Latest revision as of 15:52, 25 November 2021
In roulette, a winning number $Z$ is determined in each game by means of a ball and a roulette wheel, where we want to assume that all possible numbers $Z \in \{0, 1, 2, \ \text{...} \ , 36 \}$ are equally probable.
The players can now bet on a single number or on a group of numbers with chips of different value. Some of the possibilities and the corresponding winnings will be briefly explained here on the basis of the chips bet by a player (see graph):
- If a player bets on a number (in the example on "0"), he would get back $35$ times his stake as winnings in addition to his bet.
- If a player bets on a group of numbers with three fields (in the example, the 1-euro chip for the numbers from "22" to "24"), he would receive $ 11$ times his stake as winnings in addition to his bet.
- If a player bets on a group of numbers with $ 18$ fields (for example, the 10-euro chips on "Rouge", on "Impair" and on "Passe"), he will receive the same amount back as winnings in addition to his bet.
- If the number drawn does not belong to one of the squares he occupies, his bet is lost.
Hints:
- The exercise belongs to the chapter Set Theory Basics.
- Enter any losses as negative winnings in the following questions.
- The topic of this chapter is illustrated with examples in the (German language) learning video
- Mengentheoretische Begriffe und Gesetzmäßigkeiten $\Rightarrow$ "Set-Theoretical Concepts and Laws".
Questions
Solution
- He wins $33$ euro, if $0$ is drawn. It follows that:
- $$G_1 =\rm {36}/{37}\cdot (-1\hspace{0.1cm} euro) + {1}/{37}\cdot (33\hspace{0.1cm} euro) \hspace{0.15cm}\underline {= - 0.081\hspace{0.1cm} euro\hspace{0.1cm}(Loss)}.$$
(2) The player wins and loses nothing unless the zero is drawn. If the zero appears, he loses his bet:
- $$G_2 = \rm {1}/{37}\cdot (-2\hspace{0.1cm} euro)\hspace{0.15cm}\underline { = -0.054 \hspace{0.1cm}euro \hspace{0.1cm}(Loss)}.$$
(3) If "red" is drawn, he wins nine euro.
- If "zero" comes, he effectively wins $25$ euro.
- If "black" is drawn, he loses his entire bet of $11$ euro:
- $$G_3 = \rm {18}/{37}\cdot (10 -1) + {1}/{37}\cdot (35-10) + {18}/{37}\cdot (-10-1)\hspace{0.15cm}\underline { = - 0.297\hspace{0.1cm}euro}.$$
(4) He gets the highest winning at $Z_{\rm desire} \; \underline{ = 23} $. Then four of his five chips win:
- $$G_4 = \rm 10\hspace{0.1cm}(Red) + 10\hspace{0.1cm}(Passe) + 10\hspace{0.1cm}(Impair) + \rm 11\hspace{0.1cm}(between \hspace{0.1cm}22\hspace{0.1cm} and \hspace{0.1cm}24) - 1 \hspace{0.1cm}(not \hspace{0.1cm}0) \hspace{0.15cm}\underline {= 40 \hspace{0.1cm}euro}.$$
- If, on the other hand, the "zero" comes, he wins only $\rm 35 - 31 = 4 \ euro$.
(5) No, unfortunately not. On statistical average, the house always wins.