Difference between revisions of "Aufgaben:Exercise 1.2: Decimal/Binary Converter"
From LNTwww
| (23 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Theory_of_Stochastic_Signals/Set_Theory_Basics}} |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
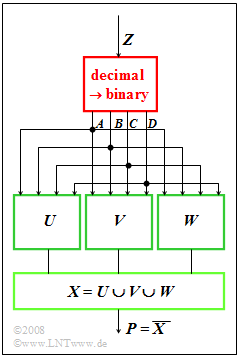
| − | === | + | [[File:EN_Sto_A_1_2.png|right|frame|Logical circuit for D/B converting]] |
| + | A number generator $Z$ supplies decimal values in the range $1$ to $15$. | ||
| + | *These are converted into binary numbers (block outlined in red). | ||
| + | *The output consists of the four binary values $A$, $B$, $C$ and $D$ with decreasing significance. | ||
| + | *For example $Z = 11$ delivers the binary values | ||
| + | :$$ A = 1, \ B = 0, \ C = 1, \ D = 1. $$ | ||
| + | Set-theoretically, this can be represented as follows: | ||
| + | :$$ Z = 11\qquad\widehat{=}\qquad A \cap\overline{ B} \cap C \cap D.$$ | ||
| + | |||
| + | Three more Boolean expressions are formed from the binary quantities $A$, $B$, $C$ and $D$ and their union set is denoted $X$ : | ||
| + | ::<math> U = A \cap \overline{D} </math> | ||
| + | ::<math> V = \overline{A} \cap B \cap \overline{D} </math> | ||
| + | :$$W,\; {\rm where} \; \, \overline{W} = \overline{A} \cup \overline{D} \cup (\overline{B} \cap C) \cup (B \cap \overline{C}). $$ | ||
| + | *Note that $Z = 0 \ ⇒ \ A = B = C = D = 0$ is already excluded by the number generator. | ||
| + | *Note also that not all input quantities $A$, $B$, $C$ and $D$ are used to calculate all intermediate quantities $U$, $V$ and $W$, resp. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | Hints: | ||
| + | *The exercise belongs to the chapter [[Theory_of_Stochastic_Signals/Mengentheoretische_Grundlagen|Set theory basic]]. | ||
| + | *The topic of this chapter is illustrated with examples in the (German language) learning video: | ||
| + | |||
| + | :[[Mengentheoretische_Begriffe_und_Gesetzmäßigkeiten_(Lernvideo)|"Mengentheoretische Begriffe und Gesetzmäßigkeiten"]] ⇒ "Set-theoretical terms and laws". | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | ===Questions=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Which statements are true regarding the random variable $U$? |
|type="[]"} | |type="[]"} | ||
| − | - $U$ | + | - $U$ contains two elements. |
| − | + $U$ | + | + $U$ contains four elements. |
| − | - | + | - The smallest element of $U$ is $4$. |
| − | + | + | + The largest element of $U$ is $14$. |
| − | { | + | {Which statements are true regarding the random variable $V$? |
|type="[]"} | |type="[]"} | ||
| − | + $V$ | + | + $V$ contains two elements. |
| − | - $V$ | + | - $V$ contains four elements. |
| − | + | + | + The smallest element of $V$ is $4$. |
| − | - | + | - The largest element of $V$ is $14$. |
| − | { | + | {Which statements are true regarding the random variable $W$? |
|type="[]"} | |type="[]"} | ||
| − | + $W$ | + | + $W$ contains two elements. |
| − | - $W$ | + | - $W$ contains four elements. |
| − | - | + | - The smallest element of $W$ is $4$. |
| − | - | + | - The largest element of $W$ is $14$. |
| − | { | + | {Which statements are true regarding the random quantity $P$ ? |
| − | |type=" | + | |type="()"} |
| − | - $P$ | + | - $P$ contains all powers of two. |
| − | + $P$ | + | + $P$ contains all prime numbers. |
| − | - $P$ | + | - $P$ describes the empty set $\phi$. |
| − | - $P$ | + | - $P$ is identical with the universal set $G = {1,2, \ \text{...} \ , 15}$. |
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | + | '''(1)''' The event $U$ contains | |
| − | + | *those numbers greater/equal to eight $(A = 1)$, | |
| − | + | *which are even $(D = 0)$: $8, 10, 12, 14$ | |
| − | + | ||
| + | |||
| + | ⇒ <u>Proposed solutions 2 and 4</u> are correct. | ||
| + | |||
| + | |||
| + | '''(2)''' The event $V$ consists of the two numbers $4$ (binary 0100) and $6$ (binary 0110) ⇒ The correct <u>solutions are 1 and 3</u>. | ||
| + | |||
| + | |||
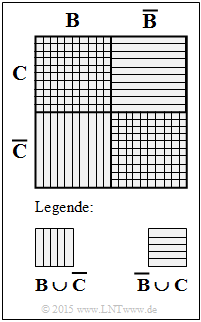
| + | [[File:P_ID2848__Sto_A_1_2c.png|right|frame|Auxiliary Venn diagram]] | ||
| + | '''(3)''' For the event $W$, de Morgan's theorem holds: | ||
| + | |||
| + | :$$\overline W = \overline A \cup \overline D \cup (\overline B \cap C) \cup (B \cap \overline C) | ||
| + | \hspace{0.3cm} \Rightarrow \hspace{0.3cm} W = \overline{\overline W} = A \cap D \cap (\overline{\overline B \cap C}) \cap (\overline{B \cap \overline C}).$$ | ||
| − | + | *Using de Morgan's theorems, it further follows: | |
| − | $ | + | :$$ W = A \cap D \cap (B \cup \overline C) \cap (\overline B \cup C).$$ |
| − | + | *Finally, using the Boolean relation $(B \cup \overline C) \cap (\overline B \cup C) = (B \cap C) \cup (\overline B \cap \overline C)$ we obtain (see sketch): | |
| − | $ W = A \cap | + | :$$W = (A \cap B \cap C \cap D) \cup (A \cap \overline B \cap \overline C \cap D).$$ |
| − | + | *Thus, $W$ contains the numbers $15$ and $9$ ⇒ only the <u>proposed solution 1</u> is correct. | |
| − | |||
| − | |||
| − | $W | + | '''(4)''' The union of $U$, $V$ and $W$ contains the following numbers: $4, 6, 8, 9, 10, 12, 14, 15$. |
| − | + | *Accordingly, the set $P$ as the complement of this union is: | |
| − | + | :$$P = {\{1, 2, 3, 5, 7, 11, 13\}}.$$ | |
| − | $P | ||
| − | + | *These are exactly the prime numbers which can be represented with four bits ⇒ <u>Proposed solution 2</u>. | |
{{ML-Fuß}} | {{ML-Fuß}} | ||
| − | [[Category: | + | [[Category:Theory of Stochastic Signals: Exercises|^1.2 Set Theory Basics^]] |
Latest revision as of 20:33, 28 November 2021
A number generator $Z$ supplies decimal values in the range $1$ to $15$.
- These are converted into binary numbers (block outlined in red).
- The output consists of the four binary values $A$, $B$, $C$ and $D$ with decreasing significance.
- For example $Z = 11$ delivers the binary values
- $$ A = 1, \ B = 0, \ C = 1, \ D = 1. $$
Set-theoretically, this can be represented as follows:
- $$ Z = 11\qquad\widehat{=}\qquad A \cap\overline{ B} \cap C \cap D.$$
Three more Boolean expressions are formed from the binary quantities $A$, $B$, $C$ and $D$ and their union set is denoted $X$ :
- \[ U = A \cap \overline{D} \]
- \[ V = \overline{A} \cap B \cap \overline{D} \]
- $$W,\; {\rm where} \; \, \overline{W} = \overline{A} \cup \overline{D} \cup (\overline{B} \cap C) \cup (B \cap \overline{C}). $$
- Note that $Z = 0 \ ⇒ \ A = B = C = D = 0$ is already excluded by the number generator.
- Note also that not all input quantities $A$, $B$, $C$ and $D$ are used to calculate all intermediate quantities $U$, $V$ and $W$, resp.
Hints:
- The exercise belongs to the chapter Set theory basic.
- The topic of this chapter is illustrated with examples in the (German language) learning video:
- "Mengentheoretische Begriffe und Gesetzmäßigkeiten" ⇒ "Set-theoretical terms and laws".
Questions
Solution
(1) The event $U$ contains
- those numbers greater/equal to eight $(A = 1)$,
- which are even $(D = 0)$: $8, 10, 12, 14$
⇒ Proposed solutions 2 and 4 are correct.
(2) The event $V$ consists of the two numbers $4$ (binary 0100) and $6$ (binary 0110) ⇒ The correct solutions are 1 and 3.
(3) For the event $W$, de Morgan's theorem holds:
- $$\overline W = \overline A \cup \overline D \cup (\overline B \cap C) \cup (B \cap \overline C) \hspace{0.3cm} \Rightarrow \hspace{0.3cm} W = \overline{\overline W} = A \cap D \cap (\overline{\overline B \cap C}) \cap (\overline{B \cap \overline C}).$$
- Using de Morgan's theorems, it further follows:
- $$ W = A \cap D \cap (B \cup \overline C) \cap (\overline B \cup C).$$
- Finally, using the Boolean relation $(B \cup \overline C) \cap (\overline B \cup C) = (B \cap C) \cup (\overline B \cap \overline C)$ we obtain (see sketch):
- $$W = (A \cap B \cap C \cap D) \cup (A \cap \overline B \cap \overline C \cap D).$$
- Thus, $W$ contains the numbers $15$ and $9$ ⇒ only the proposed solution 1 is correct.
(4) The union of $U$, $V$ and $W$ contains the following numbers: $4, 6, 8, 9, 10, 12, 14, 15$.
- Accordingly, the set $P$ as the complement of this union is:
- $$P = {\{1, 2, 3, 5, 7, 11, 13\}}.$$
- These are exactly the prime numbers which can be represented with four bits ⇒ Proposed solution 2.