Difference between revisions of "Aufgaben:Exercise 2.4: Frequency and Phase Offset"
m |
m (→Solution) |
||
| Line 77: | Line 77: | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
'''(1)''' <u>Answers 2, 3 and 5</u> are correct: | '''(1)''' <u>Answers 2, 3 and 5</u> are correct: | ||
| − | * | + | *Envelope demodulation is not applicable for ZSB-AM without carrier and a modulation depth of $m > 1$ . |
| − | * | + | *The performance of the synchronous demodulator is not increased by the additional carrier component, but only leads to an unnecessary increase in the transmit power to be applied. |
| − | * | + | *The third statement is also correct. The solution to [[Aufgaben:Exercise_2.4Z:__Low-pass_Influence_with_Synchronous_Demodulation|Exercise 2.4Z]] shows the effects of omitting or incorrectly dimensioning $H_{\rm E} (f)$ . wird gezeigt, welche Auswirkungen ein Verzicht bzw. eine falsche Dimensionierung hat. |
| − | '''(2)''' | + | '''(2)''' As the name "Synchronous demodulator” already implies, the signals $z(t)$ and $z_{\rm E} (t)$ |
| + | must be synchronous in frequency and phase: | ||
:$$f_{\rm E} = f_{\rm T} \hspace{0.15cm}\underline {= 50\,{\rm kHz}}, \hspace{0.15cm}\phi_{\rm E} = \phi_{\rm T} \hspace{0.15cm}\underline {= - 90^{\circ}} \hspace{0.05cm}.$$ | :$$f_{\rm E} = f_{\rm T} \hspace{0.15cm}\underline {= 50\,{\rm kHz}}, \hspace{0.15cm}\phi_{\rm E} = \phi_{\rm T} \hspace{0.15cm}\underline {= - 90^{\circ}} \hspace{0.05cm}.$$ | ||
| − | * | + | *The carrier frequency $f_{\rm T} $ at the transmitter can be determined from the transmission spectrum data $S(f)$ . In the case of perfect synchronisation: |
:$$v(t) = {A_{\rm E}}/{2} \cdot q(t) + {A_{\rm E}}/{2} \cdot q(t)\cdot \cos(2 \cdot \omega_{\rm T} \cdot t ) \hspace{0.05cm}.$$ | :$$v(t) = {A_{\rm E}}/{2} \cdot q(t) + {A_{\rm E}}/{2} \cdot q(t)\cdot \cos(2 \cdot \omega_{\rm T} \cdot t ) \hspace{0.05cm}.$$ | ||
| − | * | + | *The second term is removed by the low-pass filter. Thus, with $A_{\rm E}\hspace{0.15cm}\underline{ = 2}$ , $v(t) = q(t)$ holds. |
| − | '''(3)''' | + | '''(3)''' In the theory section, it was shown that in general, for DSB-AM and synchronous demodulation: |
:$$v(t) = \cos(\Delta \phi_{\rm T}) \cdot q(t) \hspace{0.05cm}.$$ | :$$v(t) = \cos(\Delta \phi_{\rm T}) \cdot q(t) \hspace{0.05cm}.$$ | ||
| − | * | + | *Even insufficient phase synchronisation does not lead to distortions, only frequency-independent attenuation. |
*Mit $ϕ_{\rm T} =-90^\circ$ und $ϕ_{\rm T} = -120^\circ$ ist $Δϕ_{\rm T} = -30^\circ$ und man erhält: | *Mit $ϕ_{\rm T} =-90^\circ$ und $ϕ_{\rm T} = -120^\circ$ ist $Δϕ_{\rm T} = -30^\circ$ und man erhält: | ||
:$$ v(t) = \cos(30^{\circ}) \cdot q(t)= 0.866 \cdot q(t) \hspace{0.3cm} \Rightarrow \hspace{0.3cm} v(t= 0) = 0.866 \cdot A_1 \hspace{0.15cm}\underline {= 1.732\,{\rm V}}\hspace{0.05cm}.$$ | :$$ v(t) = \cos(30^{\circ}) \cdot q(t)= 0.866 \cdot q(t) \hspace{0.3cm} \Rightarrow \hspace{0.3cm} v(t= 0) = 0.866 \cdot A_1 \hspace{0.15cm}\underline {= 1.732\,{\rm V}}\hspace{0.05cm}.$$ | ||
Revision as of 23:04, 29 November 2021
Consider the source signal $q(t) = A_{\rm 1} \cdot \cos(2 \pi f_{\rm 1} t ) +A_{\rm 2} \cdot \sin(2 \pi f_{\rm 2} t )$ with the signal parameters
- $$ A_1 = 2\,{\rm V}, \hspace{0.15cm}f_1 = 2\,{\rm kHz} \hspace{0.05cm},$$
- $$A_2 = 1\,{\rm V}, \hspace{0.15cm}f_2 = 5\,{\rm kHz}\hspace{0.05cm}.$$
This signal is DSB ammplitude modulated.
Thus, the modulated signal $s(t)$ has spectral components at $±45$ kHz, $±48$ kHz, $±52$ kHz and $±55$ kHz. It is also known, that the transmitter-side carrier Trägersignal is sinusoidal $(ϕ_{\rm T} = -90^\circ)$.
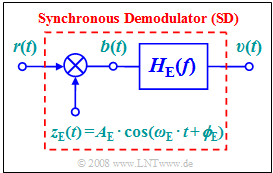
The demodulation to be performed with the circuit sketched here, which is defined by the following parameters:
- Amplitude $A_{\rm E}$ (no unit),
- Frequency $f_{\rm E}$,
- Phase $ϕ_{\rm E}$.
The $H_{\rm E}(f)$ block represents an ideal, rectangular low-pass filter, which is suitably dimensioned.
Hints:
- This exercise belongs to the chapter Synchronous Demodulation.
- Particular reference is made to the pages Influence of a frequency offset and Influence of a phase offset.
- Take the following trigonometric transformations into account:
- $$\cos(\alpha)\cdot \cos(\beta) = {1}/{2} \cdot \left[ \cos(\alpha-\beta) + \cos(\alpha+\beta)\right] \hspace{0.05cm},$$
- $$\sin(\alpha)\cdot \cos(\beta) = {1}/{2} \cdot \left[ \sin(\alpha-\beta) + \sin(\alpha+\beta)\right] \hspace{0.05cm},$$
- $$\sin(\alpha)\cdot \sin(\beta) = {1}/{2} \cdot \left[ \cos(\alpha-\beta) - \cos(\alpha+\beta)\right] \hspace{0.05cm}.$$
Questions
Solution
- Envelope demodulation is not applicable for ZSB-AM without carrier and a modulation depth of $m > 1$ .
- The performance of the synchronous demodulator is not increased by the additional carrier component, but only leads to an unnecessary increase in the transmit power to be applied.
- The third statement is also correct. The solution to Exercise 2.4Z shows the effects of omitting or incorrectly dimensioning $H_{\rm E} (f)$ . wird gezeigt, welche Auswirkungen ein Verzicht bzw. eine falsche Dimensionierung hat.
(2) As the name "Synchronous demodulator” already implies, the signals $z(t)$ and $z_{\rm E} (t)$ must be synchronous in frequency and phase:
- $$f_{\rm E} = f_{\rm T} \hspace{0.15cm}\underline {= 50\,{\rm kHz}}, \hspace{0.15cm}\phi_{\rm E} = \phi_{\rm T} \hspace{0.15cm}\underline {= - 90^{\circ}} \hspace{0.05cm}.$$
- The carrier frequency $f_{\rm T} $ at the transmitter can be determined from the transmission spectrum data $S(f)$ . In the case of perfect synchronisation:
- $$v(t) = {A_{\rm E}}/{2} \cdot q(t) + {A_{\rm E}}/{2} \cdot q(t)\cdot \cos(2 \cdot \omega_{\rm T} \cdot t ) \hspace{0.05cm}.$$
- The second term is removed by the low-pass filter. Thus, with $A_{\rm E}\hspace{0.15cm}\underline{ = 2}$ , $v(t) = q(t)$ holds.
(3) In the theory section, it was shown that in general, for DSB-AM and synchronous demodulation:
- $$v(t) = \cos(\Delta \phi_{\rm T}) \cdot q(t) \hspace{0.05cm}.$$
- Even insufficient phase synchronisation does not lead to distortions, only frequency-independent attenuation.
- Mit $ϕ_{\rm T} =-90^\circ$ und $ϕ_{\rm T} = -120^\circ$ ist $Δϕ_{\rm T} = -30^\circ$ und man erhält:
- $$ v(t) = \cos(30^{\circ}) \cdot q(t)= 0.866 \cdot q(t) \hspace{0.3cm} \Rightarrow \hspace{0.3cm} v(t= 0) = 0.866 \cdot A_1 \hspace{0.15cm}\underline {= 1.732\,{\rm V}}\hspace{0.05cm}.$$
(4) Nun beträgt die Phasendifferenz $Δϕ_{\rm T} = 90^\circ$ und man erhält $v(t) \equiv 0$.
- Es ist müßig darüber zu diskutieren, ob es sich hierbei noch immer um ein verzerrungsfreies System handelt.
- Das Ergebnis $v(t) \equiv 0$ ist darauf zurückzuführen, dass Cosinus und Sinus orthogonale Funktionen sind.
- Dieses Prinzip wird zum Beispiel bei der so genannten Quadratur–Amplitudenmodulation ausgenutzt.
(5) Hier lautet nun die Gleichung für das Signal nach der Multiplikation:
- $$b(t) = q(t) \cdot \cos(\omega_{\rm T} \cdot t - 90^{\circ}) \cdot 2 \cdot \cos(\omega_{\rm E} \cdot t - 90^{\circ})= 2 \cdot q(t) \cdot \sin(\omega_{\rm T} \cdot t ) \cdot \sin(\omega_{\rm E} \cdot t )\hspace{0.05cm}.$$
- Dieses Ergebnis kann mit der trigonometrischen Umformung
- $$\sin(\alpha)\cdot \sin(\beta) = {1}/{2} \cdot \left[ \cos(\alpha-\beta) - \cos(\alpha+\beta)\right]$$
- auch wie folgt geschrieben werden:
- $$ b(t) = q(t) \cdot \cos((\omega_{\rm T} - \omega_{\rm E}) \cdot t ) + q(t) \cdot \cos((\omega_{\rm T} + \omega_{\rm E}) \cdot t ) \hspace{0.05cm}.$$
- Der zweite Term liegt für $f_{\rm E} ≈ f_{\rm T}$ in der Umgebung von $2f_{\rm T}$ und wird durch den Tiefpass entfernt.
Somit bleibt mit der Frequenzdifferenz $Δ\hspace{-0.05cm}f_{\rm T} = f_{\rm E} - f_{\rm T}= 1$ kHz:
- $$ v(t) = q(t) \cdot \cos(2 \pi \cdot \Delta \hspace{-0.05cm}f_{\rm T} \cdot t) \hspace{0.05cm}.$$
- Die erste Aussage ist richtig. Diese besagt, dass nun das Nachrichtensignal $v(t)$ nach der Demodulation gemäß einer Cosinusfunktion leiser und wieder lauter wird („Schwebung”).
- Aus dem Cosinusanteil von $q(t)$ mit der Frequenz $f_1 = 2\text{ kHz}$ werden nun zwei Anteile (jeweils halber Amplitude) bei $1\text{ kHz}$ und $3\text{ kHz}$.
- Ebenso ist im Sinkensignal kein Anteil bei $f_2 = 5\text{ kHz}$ enthalten, sondern lediglich Anteile bei $4\text{ kHz}$ und bei $6\text{ kHz}$:
- $$1\,{\rm V} \cdot \sin(2 \pi \cdot 5\,{\rm kHz} \cdot t)\cdot \cos(2 \pi \cdot 1\,{\rm kHz} \cdot t) = 0.5\,{\rm V} \cdot \sin(2 \pi \cdot 4\,{\rm kHz} \cdot t) + 0.5\,{\rm V} \cdot \sin(2 \pi \cdot 6\,{\rm kHz} \cdot t)\hspace{0.05cm}.$$
Richtig sind somit die Aussagen 1, 3 und 4.