Difference between revisions of "Aufgaben:Exercise 1.5Z: Probabilities of Default"
From LNTwww
| (One intermediate revision by the same user not shown) | |||
| Line 37: | Line 37: | ||
$p_\text{T, max} \ = \ $ { 2 3% } $ \ \%$ | $p_\text{T, max} \ = \ $ { 2 3% } $ \ \%$ | ||
| − | {Let the default probability of all components be $\underline{p_{\rm B} = 0.1}$. Let each sub-device consist of $n = 3$ components. <br>Calculate the probability $p_{\rm T}$ exactly that a | + | {Let the default probability of all components be $\underline{p_{\rm B} = 0.1}$. Let each sub-device consist of $n = 3$ components. <br>Calculate the probability $p_{\rm T}$ exactly that a sub-device defaults. |
|type="{}"} | |type="{}"} | ||
$p_{\rm T} \ = \ $ { 27.1 3% } $ \ \%$ | $p_{\rm T} \ = \ $ { 27.1 3% } $ \ \%$ | ||
| Line 45: | Line 45: | ||
$p_{\rm T} \ = \ $ { 2.97 3% } $ \ \%$ | $p_{\rm T} \ = \ $ { 2.97 3% } $ \ \%$ | ||
| − | {Now apply $p_{\rm B} = 0.4\%$ for the default probability of all components. What is the maximum number of components the sub-device can contain? $p_{\rm T} ≤ 2\%$ is to hold. | + | {Now apply $p_{\rm B} = 0.4\%$ for the default probability of all components. What is the maximum number of components the sub-device can contain? $p_{\rm T} ≤ 2\%$ is to hold. |
|type="{}"} | |type="{}"} | ||
$n \ = \ $ { 5 3% } | $n \ = \ $ { 5 3% } | ||
| Line 54: | Line 54: | ||
===Solution=== | ===Solution=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' Since the two | + | '''(1)''' Since the two sub-devices default independently, set-theoretically holds: |
| − | :$$\rm Pr( | + | :$${\rm Pr(}G \text{ drops out)} = {\rm Pr(}T_1 \text{ drops out)} \cdot {\rm Pr(}T_2 \text{ drops out)}. $$ |
| − | *Moreover, since | + | *Moreover, since the sub-devices $T_1$ and $T_2$ are identical in construction, they default with the same probability $p_{\rm T}.$ It follows that: |
| − | :$$p_{\rm G} = \it p_{\rm T}^{\rm 2} \hspace{0.5cm} \ | + | :$$p_{\rm G} = \it p_{\rm T}^{\rm 2} \hspace{0.5cm} \Rightarrow \hspace{0.5cm} \rm \it p_{\rm T,\hspace{0.1cm}max}= \sqrt{\it p_{\rm G}} \le \rm\sqrt{0.0004} \hspace{0.15cm}\underline {= 2\%}.$$ |
| − | |||
'''(2)''' This result is easier to determine using the complementary event: | '''(2)''' This result is easier to determine using the complementary event: | ||
:$$\rm Pr(\it T_{\rm 1}\hspace{0.1cm}\rm functions) = \rm Pr(\it B_{\rm 1} \hspace{0.1cm}\rm functions \cap \it B_{\rm 2} \hspace{0.1cm} \rm functions \cap \it B_{\rm 3}\hspace{0.1cm} \rm functions).$$ | :$$\rm Pr(\it T_{\rm 1}\hspace{0.1cm}\rm functions) = \rm Pr(\it B_{\rm 1} \hspace{0.1cm}\rm functions \cap \it B_{\rm 2} \hspace{0.1cm} \rm functions \cap \it B_{\rm 3}\hspace{0.1cm} \rm functions).$$ | ||
| − | :$$\Rightarrow 1- p_{\rm T}= (1-p_{\rm | + | :$$\Rightarrow 1- p_{\rm T}= (1-p_{\rm B})^{3} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} |
1-p_{\rm T}=(0.9)^3= 0.729 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} p_{\rm T}\hspace{0.15cm}\underline {= 0.271 = 27.1\%}.$$ | 1-p_{\rm T}=(0.9)^3= 0.729 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} p_{\rm T}\hspace{0.15cm}\underline {= 0.271 = 27.1\%}.$$ | ||
| − | + | '''(3)''' With $p_{\rm B} = 0.01$, we obtain $p_{\rm T}\hspace{0.15cm}\underline {= 2.97\%}.$ | |
| − | '''(3)''' With $p_{\rm | + | *In general, the approximation is: $p_{\rm T} \approx n \cdot p_{\rm B}\; (= 3\%)$. |
| − | *In general, the approximation is: $p_{\rm T} \approx n \cdot p_{\rm | ||
| − | |||
| − | '''(4)''' With the approximation of the last | + | '''(4)''' With the approximation of the last subtask ⇒ $\underline{n = 5}$ follows directly. |
| − | *For larger $p_{\rm | + | *For larger $p_{\rm B}$, one would have to proceed as follows: |
:$$0.996^{\it n}\ge 0.98 \hspace{0.5cm} \rm\Rightarrow \hspace{0.5cm} \it n\le\rm\frac{log(0.98)}{log(0.996)} = 5.0406\hspace{0.15cm}\underline { \approx 5}.$$ | :$$0.996^{\it n}\ge 0.98 \hspace{0.5cm} \rm\Rightarrow \hspace{0.5cm} \it n\le\rm\frac{log(0.98)}{log(0.996)} = 5.0406\hspace{0.15cm}\underline { \approx 5}.$$ | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
Latest revision as of 13:26, 1 December 2021
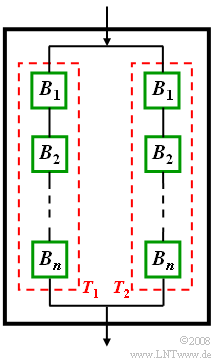
A sub-device is composed of the components $B_1, \ B_2,\ \text{...} \ , B_n$ where the respective functionality can be assumed to be independent of all other components.
- Assume that all components default with equal probability $p_{\rm B}$.
- Sub-device $T_1$ functions only if all $n$ components are functional.
To increase reliability, important assemblies are often duplicated. The overall device $G$ can be described in terms of set theory as follows:
- $$ G = T_1 \cup T_2.$$
This means: The overall device $G$ is already operational if at least one of the two identical sub-devices $(T_1$ or $T_2)$ is functional.
Hints:
- The exercise belongs to the chapter Statistical dependence and independence.
- The topic of this chapter is illustrated with examples in the (German language) learning video
- Statistische Abhängigkeit und Unabhängigkeit $\Rightarrow$ "Statistical dependence and independence".
- Explanations:
- Component (German: "Bauteil" ⇒ subscript "B")
- Sub-device (German: "Teilgerät" ⇒ subscript "T")
- Overall device (German: "Gesamtgerät" ⇒ subscript "G")
Questions
Solution
(1) Since the two sub-devices default independently, set-theoretically holds:
- $${\rm Pr(}G \text{ drops out)} = {\rm Pr(}T_1 \text{ drops out)} \cdot {\rm Pr(}T_2 \text{ drops out)}. $$
- Moreover, since the sub-devices $T_1$ and $T_2$ are identical in construction, they default with the same probability $p_{\rm T}.$ It follows that:
- $$p_{\rm G} = \it p_{\rm T}^{\rm 2} \hspace{0.5cm} \Rightarrow \hspace{0.5cm} \rm \it p_{\rm T,\hspace{0.1cm}max}= \sqrt{\it p_{\rm G}} \le \rm\sqrt{0.0004} \hspace{0.15cm}\underline {= 2\%}.$$
(2) This result is easier to determine using the complementary event:
- $$\rm Pr(\it T_{\rm 1}\hspace{0.1cm}\rm functions) = \rm Pr(\it B_{\rm 1} \hspace{0.1cm}\rm functions \cap \it B_{\rm 2} \hspace{0.1cm} \rm functions \cap \it B_{\rm 3}\hspace{0.1cm} \rm functions).$$
- $$\Rightarrow 1- p_{\rm T}= (1-p_{\rm B})^{3} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} 1-p_{\rm T}=(0.9)^3= 0.729 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} p_{\rm T}\hspace{0.15cm}\underline {= 0.271 = 27.1\%}.$$
(3) With $p_{\rm B} = 0.01$, we obtain $p_{\rm T}\hspace{0.15cm}\underline {= 2.97\%}.$
- In general, the approximation is: $p_{\rm T} \approx n \cdot p_{\rm B}\; (= 3\%)$.
(4) With the approximation of the last subtask ⇒ $\underline{n = 5}$ follows directly.
- For larger $p_{\rm B}$, one would have to proceed as follows:
- $$0.996^{\it n}\ge 0.98 \hspace{0.5cm} \rm\Rightarrow \hspace{0.5cm} \it n\le\rm\frac{log(0.98)}{log(0.996)} = 5.0406\hspace{0.15cm}\underline { \approx 5}.$$