Aufgaben:Exercise 2.5: DSB-AM via a Gaussian channel

• Return to book

DSB-AM over a distorting channel

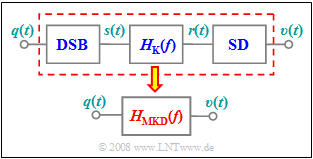
The communication system considered here is composed of the following blocks:

• DSB-AM without carrier with  $f_{\rm T} = 50 \ \rm kHz$  and  $f_{\rm T} = 55 \ \rm kHz$:

$$ s(t) = q(t) \cdot \cos (2 \pi f_{\rm T} \hspace{0.05cm} t).$$

• GGaussian bandpass channel; the magnitude  $|f|$  in the exponent causes  $H_K(–f) = H_K(f)$  to hold:

$$H_{\rm K}(f) = {\rm e}^{-\pi \cdot \hspace{0.05cm} \left (({|f| - f_{\rm M}})/{\Delta f_{\rm K}}\right)^2} ,\hspace{0.2cm} f_{\rm M} = 50\,{\rm kHz},\hspace{0.2cm} \Delta f_{\rm K} = 10\,{\rm kHz}\hspace{0.05cm}.$$

• The synchronous demodulator has optimal parameters such that the sink signal  $v(t)$  completely coincides with the source signal  $q(t)$  when  $H_{\rm K}(f) = 1$  (ideal channel).

On the page   Influence of linear channel distortions  it was shown that the entire system is is sufficiently accurately characterized by the resulting frequency response

$$H_{\rm MKD}(f) = {1}/{2} \cdot \big[ H_{\rm K}(f + f_{\rm T}) + H_{\rm K}(f - f_{\rm T})\big]$$.

Here the index stands for Modulator–K (for german "Kanal" i.e. Channel –Demodulator.

The source signal  $q(t)$  is composed of two cosine oscillations:

$$q(t) = 2\,{\rm V}\cdot \cos (2 \pi \cdot 1\,{\rm kHz} \cdot t)+ 3\,{\rm V}\cdot \cos (2 \pi \cdot 5\,{\rm kHz} \cdot t)\hspace{0.05cm}.$$

Hints:

• This exercise belongs to the chapter  Synchronous Demodulation.
• Particular reference is made to the page  Influence of linear channel distortions.

Questions

1

Berechnen Sie den resultierenden Frequenzgang  $H_{\rm MKD}(f)$  für  $f_{\rm T} = 50 \ \rm kHz$.  Welche Werte ergeben sich für  $f = 1 \ \rm kHz$  und  $f = 5 \ \rm kHz$?

$|H_{\rm MKD} (f = 1\ \rm kHz)| \ = \ $

$|H_{\rm MKD} (f = 5\ \rm kHz)| \ = \ $

2

Berechnen Sie das Sinkensignal  $v(t)$.  Geben Sie die Amplituden  $A_1$  und  $A_5$  des  $1\ \rm kHz$– bzw.  $5\ \rm kHz$–Anteils an.

$A_1 \ = \ $ $\ \text{ V }$

$A_5 \ = \ $ $\ \text{ V }$

3

Berechnen Sie den resultierenden Frequenzgang  $H_{\rm MKD}(f)$  für  $f_{\rm T} = 55 \ \rm kHz$.  Welche Werte ergeben sich nun für  $f = 1 \ \rm kHz$  und  $f = 5 \ \rm kHz$?

$|H_{\rm MKD} (f = 1\ \rm kHz)| \ = \ $

$|H_{\rm MKD} (f = 5\ \rm kHz)| \ = \ $

4

Berechnen Sie das Sinkensignal  $v(t)$.  Geben Sie hierfür die Amplituden  $A_1$  und  $A_5$  des  $1\ \rm kHz$– bzw.  $5\ \rm kHz$–Anteils an.

$A_1 \ = \ $ $\ \text{ V }$

$A_5 \ = \ $ $\ \text{ V }$

5

Gibt es eine Trägerfrequenz  $f_{\rm T}$, die bei dem gegebenen Quellensignal und dem gegebenen Kanal zu keinen Verzerrungen führt?  Begründen Sie Ihre Antwort.

	Ja,
	Nein.

Musterlösung

Solution

Resulierender Basisbandfrequenzgang für  $f_{\rm T} = f_{\rm M}$

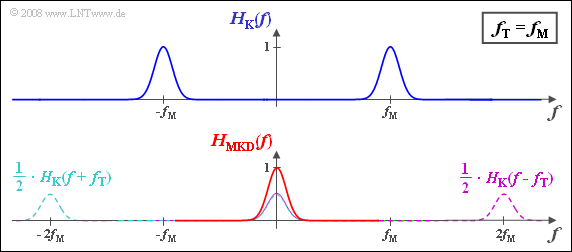
(1)  Die angegebene Gleichung besagt, dass der BP–Frequenzgang  $H_{\rm K}(f)$  jeweils um die Trägerfrequenz  $f_{\rm T}$  nach links und rechts verschoben und die beiden Anteile aufaddiert werden müssen. 

• Es ist noch der Faktor  $1/2$  zu berücksichtigen (siehe Skizze).

• Bei niedrigen Frequenzen ergibt sich dann eine Gaußfunktion um die Mittenfrequenz „0”:

$$H_{\rm MKD}(f) = {\rm e}^{-\pi \cdot \hspace{0.05cm} \left ({f}/{\Delta f_{\rm K}}\right)^2} \hspace{0.05cm}.$$

• Die beiden Anteile bei  $±2f_{\rm T}$  müssen nicht weiter betrachtet werden.  Für die zwei gesuchten Frequenzen  $f_1 = 1\ \rm kHz$  und  $f_5 = 5 \ \rm kHz$  erhält man:

$$ H_{\rm MKD}(f = f_1) = {\rm e}^{-\pi \cdot \hspace{0.05cm} \left (\frac{1\,{\rm kHz}}{10\,{\rm kHz}}\right)^2} = {\rm e}^{-\pi/100}\hspace{0.15cm}\underline {\approx 0.969} \hspace{0.05cm},$$

$$H_{\rm MKD}(f = f_5) = {\rm e}^{-\pi \cdot \hspace{0.05cm} \left (\frac{5\,{\rm kHz}}{10\,{\rm kHz}}\right)^2} = {\rm e}^{-\pi/4} \hspace{0.3cm}\hspace{0.15cm}\underline {\approx 0.456} \hspace{0.05cm}.$$

(2)  Mit  $ω_1 = 2π · 1\ \rm kHz$  und  $ω_5 = 2π · 5 \ \rm kHz$  gilt:

$$ v(t) = 0.969 \cdot 2\,{\rm V}\cdot \cos (\omega_1 \cdot t)+ 0.456 \cdot 3\,{\rm V}\cdot \cos (\omega_5 \cdot t) = \underline { 1.938\,{\rm V}}\cdot \cos (\omega_1 \cdot t) + \hspace{0.15cm}\underline {1.368\,{\rm V}}\cdot \cos (\omega_5 \cdot t) \hspace{0.05cm}.$$

• Man erkennt, dass nun –  im Gegensatz zum Quellensignal  $q(t)$  – der Anteil bei  $1 \ \rm kHz$   ⇒   $A_1 = 1.938 \ \rm V$  größer ist als der  $5 \ \rm kHz$–Anteil   ⇒   $A_5 = 1.368 \ \rm V$, da der Kanal die Frequenzen  $49 \ \rm kHz$  und  $51 \ \rm kHz$  weniger dämpft als die Spektralanteile bei  $45 \ \rm kHz$  und  $55 \ \rm kHz$.

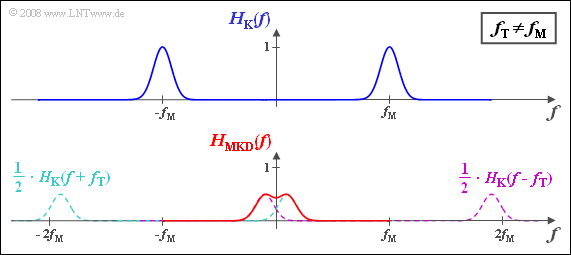
(3)  Die beiden um  $±f_{\rm T}$  verschobenen Spektralfunktionen kommen nun nicht mehr direkt übereinander zu liegen, sondern sind um  $10 \ \rm kHz$  gegeneinander versetzt.

• Der resultierende Frequenzgang  $H_{\rm MKD}(f)$  ist somit nicht mehr gaußförmig, sondern es gilt entsprechend der unteren Skizze:

$$H_{\rm MKD}(f ) = {1}/{2}\cdot \left[{\rm e}^{-\pi \cdot \hspace{0.05cm} \left (\frac{f - 5\,{\rm kHz}}{10\,{\rm kHz}}\right)^2}+{\rm e}^{-\pi \cdot \hspace{0.05cm} \left (\frac{f + 5\,{\rm kHz}}{10\,{\rm kHz}}\right)^2}\right]\hspace{0.05cm}.$$

• Für die Frequenzen  $f_1$  und  $f_5$  erhält man:

$$H_{\rm MKD}(f = 1\,{\rm kHz}) = \frac{1}{2} \cdot \left[ H_{\rm K}(f = 56\,{\rm kHz}) + H_{\rm K}(f = -54\,{\rm kHz})\right]=$$

$$\hspace{1.25cm}= \frac{1}{2}\cdot \left[{\rm e}^{-\pi \cdot \hspace{0.05cm} \left (\frac{56\, {\rm kHz}- 50\,{\rm kHz}}{10\,{\rm kHz}}\right)^2}+{\rm e}^{-\pi \cdot \hspace{0.05cm} \left (\frac{-54\, {\rm kHz}+ 50\,{\rm kHz}}{10\,{\rm kHz}}\right)^2}\right] = 0.161 + 0.302 \hspace{0.15cm}\underline {= 0.463}\hspace{0.05cm},$$

$$H_{\rm MKD}(f = 5\,{\rm kHz}) = \frac{1}{2} \cdot \left[ H_{\rm K}(f = 60\,{\rm kHz}) + H_{\rm K}(f = -50\,{\rm kHz})\right]= \hspace{0.75cm}$$

$$\hspace{1.25cm}= \frac{1}{2}\cdot \left[{\rm e}^{-\pi \cdot \hspace{0.05cm} \left (\frac{60\, {\rm kHz}- 50\,{\rm kHz}}{10\,{\rm kHz}}\right)^2}+{\rm e}^{-\pi \cdot \hspace{0.05cm} \left (\frac{-50\, {\rm kHz}+ 50\,{\rm kHz}}{10\,{\rm kHz}}\right)^2}\right] = 0.022 + 0.500 \hspace{0.15cm}\underline {= 0.521}\hspace{0.05cm}.$$

Resulierender Basisbandfrequenzgang für $f_{\rm T} \ne f_{\rm M}$

• Während bei  $f_{\rm T} = f_{\rm M} = 50 \ \rm kHz$  der Synchrondemodulator die Information über das Nachrichtensignal aus beiden Seitenbändern in gleicher Weise gewinnt, liefert mit  $f_{\rm T} = 55\ \rm kHz$  das untere Seitenband (USB) den größeren Beitrag.

• Zum Beispiel liegt das USB des  $5 \ \rm kHz$–Anteils nun genau bei  $f_{\rm M} = 50 \ \rm kHz$  und wird ungedämpft übertragen, während das OSB bei  $60 \ \rm kHz$  starken Dämpfungen unterliegt.

(4)  Mit dem Ergebnis der letzten Teilaufgabe erhält man:

$$ A_1 = 0.463 \cdot 2\,{\rm V}\hspace{0.15cm}\underline { = 0.926\,{\rm V}}\hspace{0.05cm},$$

$$A_5 = 0.521 \cdot 3\,{\rm V} \hspace{0.15cm}\underline {= 1.563\,{\rm V}}\hspace{0.05cm}.$$

• In diesem Fall sind die linearen Verzerrungen sogar weniger stark, da nun auch der  $1 \ \rm kHz$–Anteil stärker gedämpft wird.

(5)  Richtig ist JA:

• Mit der Trägerfrequenz  $f_{\rm T} = f_{\rm M} = 50 \ \rm kHz$  wird der  $5 \ \rm kHz$–Anteil stärker gedämpft als der  $1 \ \rm kHz$–Anteil, während mit  $f_{\rm T} = 55 \ {\rm kHz} \ne f_{\rm M}$  der  $1 \ \rm kHz$–Anteil etwas mehr gedämpft wird.
• Wählt man nun zum Beispiel  $f_{\rm T} \approx 54.5 \ \rm kHz$, so werden beide Anteile gleich gedämpft  $($etwa um den Faktor $0.53)$  und es gibt keine / weniger Verzerrungen.
• Dieses Ergebnis gilt allerdings nur für das betrachtete Quellensignal.  Ein anderes  $q(t)$  mit ebenfalls zwei Spektralanteilen würde eine andere „optimale Trägerfrequenz” erfordern.
• Bei einem Nachrichtensignal mit drei oder mehr Spektrallinien würde es stets zu linearen Verzerrungen kommen.