Difference between revisions of "Aufgaben:Exercise 3.7: Synchronous Demodulator"
(Die Seite wurde neu angelegt: „ {{quiz-Header|Buchseite=*Buch*/*Kapitel* }} ===Fragebogen=== <quiz display=simple> {Multiple-Choice Frage |type="[]"} - Falsch + Richtig {Input-Box Frage |…“) |
|||
| Line 2: | Line 2: | ||
{{quiz-Header|Buchseite=*Buch*/*Kapitel* | {{quiz-Header|Buchseite=*Buch*/*Kapitel* | ||
}} | }} | ||
| + | |||
| + | [[File:P_ID529__Sig_A_3_7_neu.png|250px|right|Synchrondemodulator (Aufgabe A3.7)]] | ||
| + | |||
| + | Zur Rücksetzung eines amplitudenmodulierten Signals in den ursprünglichen Frequenzbereich verwendet man oft einen Synchrondemodulator. | ||
| + | Dieser multipliziert das AM-Eingangssignal r(t) mit einem empfangsseitigen Trägersignal zE(t), das sowohl hinsichtlich der Frequenz fT als auch der Phase φT mit dem sendeseitigen Trägersignal zS(t) übereinstimmen sollte. | ||
| + | Anschließend folgt ein rechteckförmiger Tiefpass zur Eliminierung aller spektralen Anteile oberhalb der Trägerfrequenz fT. Das Ausgangssignal des Synchrondemodulators nennen wir υ(t). | ||
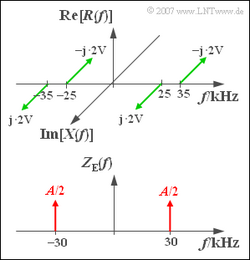
| + | Das oben skizzierte Spektrum R(f) des Empfangssignals r(t) ist durch Zweiseitenband–Amplitudenmodulation eines sinusförmigen Quellensignals q(t) mit der Frequenz 5 kHz und der Amplitude 8 V entstanden. Als sendeseitiges Trägersignal zS(t) wurde ein Cosinussignal mit der Frequenz 30 kHz verwendet. | ||
| + | Das Spektrum des empfangsseitigen Trägersignals zE(t) besteht entsprechend der unteren Skizze aus zwei Diraclinien, jeweils mit dem Gewicht A/2. Da zE(t) keine Einheit beinhalten soll, sind auch die Gewichte der Diracfunktionen dimensionslos. | ||
| + | Hinweis: Die Aufgabe bezieht sich auf die theoretischen Grundlagen entsprechend Kapitel 3.4, insbesondere auf die Seite Faltung einer Funktion mit einer Diracfunktion. | ||
| + | |||
===Fragebogen=== | ===Fragebogen=== | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Es gelte fT = 30 kHz und A = 1. Berechnen Sie das Ausgangssignal υ(t). Welcher Signalwert tritt zum Zeitpunkt t = 50 µs auf? |
| − | |type=" | + | |type="{}"} |
| − | + | $v(t=50 \mu \text{s}) =$ { 4 } V | |
| − | |||
| + | {Wie groß muss die Amplitude des empfangsseitigen Trägersignals zE(t) gewählt werden, damit υ(t) = q(t) gilt? | ||
| + | |type="{}"} | ||
| + | $A =$ { 2 } | ||
| − | { | + | {Berechnen Sie das Ausgangssignal υ(t) unter den Voraussetzungen A = 2 und fT = 31 kHz. Welcher Signalwert tritt zum Zeitpunkt t = 50 µs auf? |
|type="{}"} | |type="{}"} | ||
| − | + | $v(t=50 \mu \text{s}) =$ { 7.608 } V | |
| − | |||
| − | |||
</quiz> | </quiz> | ||
===Musterlösung=== | ===Musterlösung=== | ||
| + | |||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''1.''' | + | '''1.''' a) Benennen wir das Signal nach dem Multiplizierer mit m(t) = r(t) · zE(t), so ergibt sich das zugehörige Spektrum M(f) als das Faltungsprodukt aus R(f) und ZE(f). Die Faltung des Spektrums R(f) mit der rechten Diraclinie bei +30 kHz führt zu diskreten Spektrallinien bei –5 kHz, 5 kHz, 55 kHz und 65 kHz. Diese sind alle imaginär und gegenüber den Impulsgewichten von R(f) um den Faktor A/2 = 0.5 kleiner. Die Faltung von R(f) mit dem Dirac bei –30 kHz ergibt Linien bei –65 kHz, –55 kHz, –5 kHz, 5 kHz. |
| + | Durch Überlagerung der beiden Zwischenresultate und Berücksichtigung des Tiefpassfilters, der die Linien bei ±55 kHz und ±65 kHz unterdrückt, folgt somit für das Spektrum des Sinkensignals: | ||
| + | |||
| + | $$V( f) = - {\rm{j}} \cdot 2\;{\rm{V}} \cdot \delta ( {f - f_{\rm N} }) + {\rm{j}} \cdot 2\;{\rm{V}} \cdot \delta ( {f + f_{\rm N} } )\hspace{0.3cm}{\rm mit}\hspace{0.3cm}f_{\rm N} = 5\;{\rm kHz}.$$ | ||
| + | |||
| + | Das Sinkensignal υ(t) ist also ein 5 kHz–Sinussignal mit der Amplitude 4 V. Der Zeitpunkt t = 50 µs entspricht einem Viertel der Periodendauer. Somit ist hier das Sinkensignal maximal, also 4 V. | ||
| + | b) Mit A = 1 ist υ(t) = q(t)/2. Dagegen sind mit A = 2 beide Signale gleich. | ||
| + | c) Die beiden Diraclinien bei ±fT haben nun jeweils das Gewicht 1. Alle nachfolgend genannten Spektrallinien sind imaginär und betragsmäßig gleich 2 V. Die Faltung von R(f) mit der rechten Diraclinie von zE(t) liefert Anteile bei –4 kHz (p: positiv), 6 kHz (n: negativ), 56 kHz (p) und 66 kHz (n). | ||
| + | Dagegen führt die Faltung mit der linken Diracfunktion zu Spektrallinien bei –66 kHz (p), –56 kHz (n), –6 kHz (p) und 4 kHz (n), alle ebenfalls mit den (betragsmäßigen) Impulsgewichten 2 V. Unter Berücksichtigung des Tiefpasses verbleiben nur die vier Spektrallinien bei ±4 kHz und ±6 kHz. Das dazugehörige Zeitsignal lautet mit f4 = 4 kHz und f6 = 6 kHz: | ||
| + | |||
| + | Zum Zeitpunkt t = 50 µs erhält man: | ||
| + | |||
{{ML-Fuß}} | {{ML-Fuß}} | ||
__NOEDITSECTION__ | __NOEDITSECTION__ | ||
[[Category:Aufgaben zu Signaldarstellung|^3. Aperiodische Signale - Impulse^]] | [[Category:Aufgaben zu Signaldarstellung|^3. Aperiodische Signale - Impulse^]] | ||
Revision as of 23:48, 17 April 2016
Zur Rücksetzung eines amplitudenmodulierten Signals in den ursprünglichen Frequenzbereich verwendet man oft einen Synchrondemodulator. Dieser multipliziert das AM-Eingangssignal r(t) mit einem empfangsseitigen Trägersignal zE(t), das sowohl hinsichtlich der Frequenz fT als auch der Phase φT mit dem sendeseitigen Trägersignal zS(t) übereinstimmen sollte. Anschließend folgt ein rechteckförmiger Tiefpass zur Eliminierung aller spektralen Anteile oberhalb der Trägerfrequenz fT. Das Ausgangssignal des Synchrondemodulators nennen wir υ(t). Das oben skizzierte Spektrum R(f) des Empfangssignals r(t) ist durch Zweiseitenband–Amplitudenmodulation eines sinusförmigen Quellensignals q(t) mit der Frequenz 5 kHz und der Amplitude 8 V entstanden. Als sendeseitiges Trägersignal zS(t) wurde ein Cosinussignal mit der Frequenz 30 kHz verwendet. Das Spektrum des empfangsseitigen Trägersignals zE(t) besteht entsprechend der unteren Skizze aus zwei Diraclinien, jeweils mit dem Gewicht A/2. Da zE(t) keine Einheit beinhalten soll, sind auch die Gewichte der Diracfunktionen dimensionslos. Hinweis: Die Aufgabe bezieht sich auf die theoretischen Grundlagen entsprechend Kapitel 3.4, insbesondere auf die Seite Faltung einer Funktion mit einer Diracfunktion.
Fragebogen
Musterlösung
$$V( f) = - {\rm{j}} \cdot 2\;{\rm{V}} \cdot \delta ( {f - f_{\rm N} }) + {\rm{j}} \cdot 2\;{\rm{V}} \cdot \delta ( {f + f_{\rm N} } )\hspace{0.3cm}{\rm mit}\hspace{0.3cm}f_{\rm N} = 5\;{\rm kHz}.$$
Das Sinkensignal υ(t) ist also ein 5 kHz–Sinussignal mit der Amplitude 4 V. Der Zeitpunkt t = 50 µs entspricht einem Viertel der Periodendauer. Somit ist hier das Sinkensignal maximal, also 4 V. b) Mit A = 1 ist υ(t) = q(t)/2. Dagegen sind mit A = 2 beide Signale gleich. c) Die beiden Diraclinien bei ±fT haben nun jeweils das Gewicht 1. Alle nachfolgend genannten Spektrallinien sind imaginär und betragsmäßig gleich 2 V. Die Faltung von R(f) mit der rechten Diraclinie von zE(t) liefert Anteile bei –4 kHz (p: positiv), 6 kHz (n: negativ), 56 kHz (p) und 66 kHz (n). Dagegen führt die Faltung mit der linken Diracfunktion zu Spektrallinien bei –66 kHz (p), –56 kHz (n), –6 kHz (p) und 4 kHz (n), alle ebenfalls mit den (betragsmäßigen) Impulsgewichten 2 V. Unter Berücksichtigung des Tiefpasses verbleiben nur die vier Spektrallinien bei ±4 kHz und ±6 kHz. Das dazugehörige Zeitsignal lautet mit f4 = 4 kHz und f6 = 6 kHz:
Zum Zeitpunkt t = 50 µs erhält man: