Difference between revisions of "Aufgaben:Exercise 2.5: DSB-AM via a Gaussian channel"
m |
|||
| (3 intermediate revisions by the same user not shown) | |||
| Line 4: | Line 4: | ||
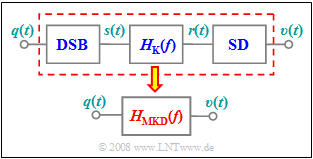
[[File:EN_Mod_A_2_5.png|right|frame|DSB-AM over a distorting channel]] | [[File:EN_Mod_A_2_5.png|right|frame|DSB-AM over a distorting channel]] | ||
The communication system considered here is composed of the following blocks: | The communication system considered here is composed of the following blocks: | ||
| − | *DSB-AM without carrier | + | *DSB-AM without carrier $(f_{\rm T} = 50 \ \rm kHz$ or $f_{\rm T} = 55 \ \rm kHz)$: |
:$$ s(t) = q(t) \cdot \cos (2 \pi f_{\rm T} \hspace{0.05cm} t).$$ | :$$ s(t) = q(t) \cdot \cos (2 \pi f_{\rm T} \hspace{0.05cm} t).$$ | ||
| − | * Gaussian | + | * Gaussian band-pass channel; the magnitude $|f|$ in the exponent causes $H_K(–f) = H_K(f)$ to hold: |
:$$H_{\rm K}(f) = {\rm e}^{-\pi \cdot \hspace{0.05cm} \left (({|f| - f_{\rm M}})/{\Delta f_{\rm K}}\right)^2} ,\hspace{0.2cm} f_{\rm M} = 50\,{\rm kHz},\hspace{0.2cm} \Delta f_{\rm K} = 10\,{\rm kHz}\hspace{0.05cm}.$$ | :$$H_{\rm K}(f) = {\rm e}^{-\pi \cdot \hspace{0.05cm} \left (({|f| - f_{\rm M}})/{\Delta f_{\rm K}}\right)^2} ,\hspace{0.2cm} f_{\rm M} = 50\,{\rm kHz},\hspace{0.2cm} \Delta f_{\rm K} = 10\,{\rm kHz}\hspace{0.05cm}.$$ | ||
| − | *The synchronous demodulator has optimal parameters such that the sink signal $v(t)$ completely coincides with the source signal $q(t)$ when $H_{\rm K}(f) = 1$ (ideal channel). | + | *The synchronous demodulator has optimal parameters such that the sink signal $v(t)$ completely coincides with the source signal $q(t)$ when $H_{\rm K}(f) = 1$ ("ideal channel"). |
On the page [[Modulation_Methods/Synchronous_Demodulation#Influence_of_linear_channel_distortions| Influence of linear channel distortions]] it was shown that the entire system is is sufficiently accurately characterized by the resulting frequency response | On the page [[Modulation_Methods/Synchronous_Demodulation#Influence_of_linear_channel_distortions| Influence of linear channel distortions]] it was shown that the entire system is is sufficiently accurately characterized by the resulting frequency response | ||
:$$H_{\rm MKD}(f) = {1}/{2} \cdot \big[ H_{\rm K}(f + f_{\rm T}) + H_{\rm K}(f - f_{\rm T})\big]$$ | :$$H_{\rm MKD}(f) = {1}/{2} \cdot \big[ H_{\rm K}(f + f_{\rm T}) + H_{\rm K}(f - f_{\rm T})\big]$$ | ||
| − | Here the | + | Here the subscript stands for $\rm M$odulator – $\rm K$ (for German "Kanal" i.e. channel) – $\rm D$emodulator. |
The source signal $q(t)$ is composed of two cosine oscillations: | The source signal $q(t)$ is composed of two cosine oscillations: | ||
| Line 23: | Line 23: | ||
| − | + | Hints: | |
| − | |||
| − | |||
| − | |||
*This exercise belongs to the chapter [[Modulation_Methods/Synchronous_Demodulation|Synchronous Demodulation]]. | *This exercise belongs to the chapter [[Modulation_Methods/Synchronous_Demodulation|Synchronous Demodulation]]. | ||
*Particular reference is made to the page [[Modulation_Methods/Synchronous_Demodulation#Influence_of_linear_channel_distortions|Influence of linear channel distortions]]. | *Particular reference is made to the page [[Modulation_Methods/Synchronous_Demodulation#Influence_of_linear_channel_distortions|Influence of linear channel distortions]]. | ||
| Line 36: | Line 33: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Calculate the resulting frequency response $H_{\rm MKD}(f)$ for | + | {Calculate the resulting frequency response $H_{\rm MKD}(f)$ for $f_{\rm T} = 50 \ \rm kHz$. |
| − | What are the values for | + | What are the values for $f = 1 \ \rm kHz$ and $f = 5 \ \rm kHz$? |
|type="{}"} | |type="{}"} | ||
$|H_{\rm MKD} (f = 1\ \rm kHz)| \ = \ $ { 0.969 3% } | $|H_{\rm MKD} (f = 1\ \rm kHz)| \ = \ $ { 0.969 3% } | ||
$|H_{\rm MKD} (f = 5\ \rm kHz)| \ = \ $ { 0.456 3% } | $|H_{\rm MKD} (f = 5\ \rm kHz)| \ = \ $ { 0.456 3% } | ||
| − | {Calculate the sink signal $v(t)$. | + | {Calculate the sink signal $v(t)$. Specify the amplitudes $A_1$ and $A_5$ of the $1\ \rm kHz$ component and the $5\ \rm kHz$ component. |
|type="{}"} | |type="{}"} | ||
$A_1 \ = \ $ { 1.938 3% } $\ \text{ V }$ | $A_1 \ = \ $ { 1.938 3% } $\ \text{ V }$ | ||
| Line 48: | Line 45: | ||
| − | {Calculate the resulting frequency response $H_{\rm MKD}(f)$ for $f_{\rm T} = 55 \ \rm kHz$. Now, what are the values for $f = 1 \ \rm kHz$ and $f = 5 \ \rm kHz$? | + | {Calculate the resulting frequency response $H_{\rm MKD}(f)$ for $f_{\rm T} = 55 \ \rm kHz$. Now, what are the values for $f = 1 \ \rm kHz$ and $f = 5 \ \rm kHz$? |
|type="{}"} | |type="{}"} | ||
$|H_{\rm MKD} (f = 1\ \rm kHz)| \ = \ $ { 0.463 3% } | $|H_{\rm MKD} (f = 1\ \rm kHz)| \ = \ $ { 0.463 3% } | ||
$|H_{\rm MKD} (f = 5\ \rm kHz)| \ = \ $ { 0.521 3% } | $|H_{\rm MKD} (f = 5\ \rm kHz)| \ = \ $ { 0.521 3% } | ||
| − | {Calculate the sink signal $v(t)$. | + | {Calculate the sink signal $v(t)$. Specify the amplitudes $A_1$ and $A_5$ of the two components. |
|type="{}"} | |type="{}"} | ||
$A_1 \ = \ $ { 0.926 3% } $\ \text{ V }$ | $A_1 \ = \ $ { 0.926 3% } $\ \text{ V }$ | ||
$A_5 \ = \ $ { 1.563 3% } $\ \text{ V }$ | $A_5 \ = \ $ { 1.563 3% } $\ \text{ V }$ | ||
| − | {Is there a carrier frequency | + | {Is there a carrier frequency $f_{\rm T}$ that results in no distortion for the given source signal and channel? Justify your answer. |
|type="()"} | |type="()"} | ||
+ Yes, | + Yes, | ||
| Line 69: | Line 66: | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
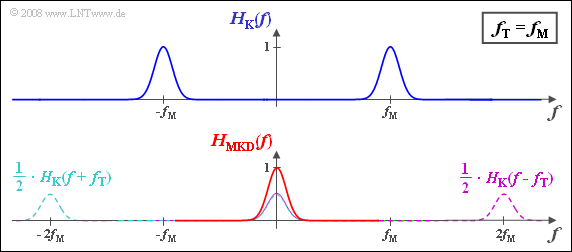
[[File:P_ID1011__Mod_A_2_5_a.png|right|frame|Resulting baseband frequency response for $f_{\rm T} = f_{\rm M}$]] | [[File:P_ID1011__Mod_A_2_5_a.png|right|frame|Resulting baseband frequency response for $f_{\rm T} = f_{\rm M}$]] | ||
| − | '''(1)''' The equation given states that the | + | '''(1)''' The equation given states that the band-pass frequency response $H_{\rm K}(f)$ has to be shifted to left and to right by the carrier frequency $f_{\rm T}$, and the two components have to be added up. |
| − | *The factor $1/2$ must still be taken into account (see plot). | + | *The factor $1/2$ must still be taken into account (see plot). |
| − | *At low frequencies, this results in a Gaussian function around the center frequency "0": | + | *At low frequencies, this results in a Gaussian function around the center frequency "0": |
:$$H_{\rm MKD}(f) = {\rm e}^{-\pi \cdot \hspace{0.05cm} \left ({f}/{\Delta f_{\rm K}}\right)^2} \hspace{0.05cm}.$$ | :$$H_{\rm MKD}(f) = {\rm e}^{-\pi \cdot \hspace{0.05cm} \left ({f}/{\Delta f_{\rm K}}\right)^2} \hspace{0.05cm}.$$ | ||
| − | *The two components at $±2f_{\rm T}$ need not be considered further. For the two frequencies we are looking for $f_1 = 1\ \rm kHz$ and $f_5 = 5 \ \rm kHz$ | + | *The two components at $±2f_{\rm T}$ need not be considered further. For the two frequencies we are looking for $f_1 = 1\ \rm kHz$ and $f_5 = 5 \ \rm kHz$, we obtain: |
:$$ H_{\rm MKD}(f = f_1) = {\rm e}^{-\pi \cdot \hspace{0.05cm} \left (\frac{1\,{\rm kHz}}{10\,{\rm kHz}}\right)^2} = {\rm e}^{-\pi/100}\hspace{0.15cm}\underline {\approx 0.969} \hspace{0.05cm},$$ | :$$ H_{\rm MKD}(f = f_1) = {\rm e}^{-\pi \cdot \hspace{0.05cm} \left (\frac{1\,{\rm kHz}}{10\,{\rm kHz}}\right)^2} = {\rm e}^{-\pi/100}\hspace{0.15cm}\underline {\approx 0.969} \hspace{0.05cm},$$ | ||
:$$H_{\rm MKD}(f = f_5) = {\rm e}^{-\pi \cdot \hspace{0.05cm} \left (\frac{5\,{\rm kHz}}{10\,{\rm kHz}}\right)^2} = {\rm e}^{-\pi/4} \hspace{0.3cm}\hspace{0.15cm}\underline {\approx 0.456} \hspace{0.05cm}.$$ | :$$H_{\rm MKD}(f = f_5) = {\rm e}^{-\pi \cdot \hspace{0.05cm} \left (\frac{5\,{\rm kHz}}{10\,{\rm kHz}}\right)^2} = {\rm e}^{-\pi/4} \hspace{0.3cm}\hspace{0.15cm}\underline {\approx 0.456} \hspace{0.05cm}.$$ | ||
| Line 80: | Line 77: | ||
| − | '''(2)''' With $ω_1 = 2π · 1\ \rm kHz$ and $ω_5 = 2π · 5 \ \rm kHz$ | + | '''(2)''' With $ω_1 = 2π · 1\ \rm kHz$ and $ω_5 = 2π · 5 \ \rm kHz$, it holds that: |
:$$ v(t) = 0.969 \cdot 2\,{\rm V}\cdot \cos (\omega_1 \cdot t)+ 0.456 \cdot 3\,{\rm V}\cdot \cos (\omega_5 \cdot t) = \underline { 1.938\,{\rm V}}\cdot \cos (\omega_1 \cdot t) + \hspace{0.15cm}\underline {1.368\,{\rm V}}\cdot \cos (\omega_5 \cdot t) \hspace{0.05cm}.$$ | :$$ v(t) = 0.969 \cdot 2\,{\rm V}\cdot \cos (\omega_1 \cdot t)+ 0.456 \cdot 3\,{\rm V}\cdot \cos (\omega_5 \cdot t) = \underline { 1.938\,{\rm V}}\cdot \cos (\omega_1 \cdot t) + \hspace{0.15cm}\underline {1.368\,{\rm V}}\cdot \cos (\omega_5 \cdot t) \hspace{0.05cm}.$$ | ||
| − | *It can be seen that now | + | *It can be seen that now – unlike the source signal $q(t)$ – the component at $1 \ \rm kHz$ ⇒ $A_1 = 1.938 \ \rm V$ is larger than the $5 \ \rm kHz$ component ⇒ $A_5 = 1.368 \ \rm V$, because the channel attenuates the $49 \ \rm kHz$ and $51 \ \rm kHz$ frequencies less than the spectral components at $45 \ \rm kHz$ and $55 \ \rm kHz$. |
| − | '''(3)''' The two spectral functions shifted by $±f_{\rm T}$ now no longer come to lie directly on top of each other, but are offset from each other by $10 \ \rm kHz$ . | + | '''(3)''' The two spectral functions shifted by $±f_{\rm T}$ now no longer come to lie directly on top of each other, but there are an offset from each other by $10 \ \rm kHz$ . |
| − | *The resulting frequency response $H_{\rm MKD}(f)$ is thus no longer Gaussian, but characterized according to the sketch below: | + | *The resulting frequency response $H_{\rm MKD}(f)$ is thus no longer Gaussian, but characterized according to the sketch below: |
:$$H_{\rm MKD}(f ) = {1}/{2}\cdot \left[{\rm e}^{-\pi \cdot \hspace{0.05cm} \left (\frac{f - 5\,{\rm kHz}}{10\,{\rm kHz}}\right)^2}+{\rm e}^{-\pi \cdot \hspace{0.05cm} \left (\frac{f + 5\,{\rm kHz}}{10\,{\rm kHz}}\right)^2}\right]\hspace{0.05cm}.$$ | :$$H_{\rm MKD}(f ) = {1}/{2}\cdot \left[{\rm e}^{-\pi \cdot \hspace{0.05cm} \left (\frac{f - 5\,{\rm kHz}}{10\,{\rm kHz}}\right)^2}+{\rm e}^{-\pi \cdot \hspace{0.05cm} \left (\frac{f + 5\,{\rm kHz}}{10\,{\rm kHz}}\right)^2}\right]\hspace{0.05cm}.$$ | ||
| Line 97: | Line 94: | ||
:$$\hspace{1.25cm}= \frac{1}{2}\cdot \left[{\rm e}^{-\pi \cdot \hspace{0.05cm} \left (\frac{60\, {\rm kHz}- 50\,{\rm kHz}}{10\,{\rm kHz}}\right)^2}+{\rm e}^{-\pi \cdot \hspace{0.05cm} \left (\frac{-50\, {\rm kHz}+ 50\,{\rm kHz}}{10\,{\rm kHz}}\right)^2}\right] = 0.022 + 0.500 \hspace{0.15cm}\underline {= 0.521}\hspace{0.05cm}.$$ | :$$\hspace{1.25cm}= \frac{1}{2}\cdot \left[{\rm e}^{-\pi \cdot \hspace{0.05cm} \left (\frac{60\, {\rm kHz}- 50\,{\rm kHz}}{10\,{\rm kHz}}\right)^2}+{\rm e}^{-\pi \cdot \hspace{0.05cm} \left (\frac{-50\, {\rm kHz}+ 50\,{\rm kHz}}{10\,{\rm kHz}}\right)^2}\right] = 0.022 + 0.500 \hspace{0.15cm}\underline {= 0.521}\hspace{0.05cm}.$$ | ||
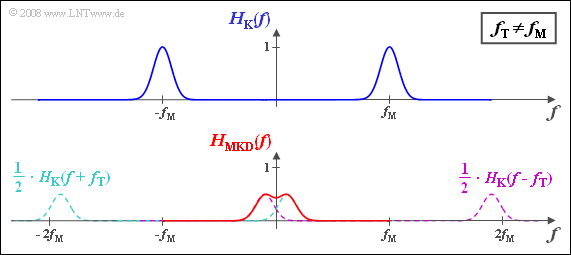
[[File:P_ID1012__Mod_A_2_5_c.png|right|frame|Resulting baseband frequency response for $f_{\rm T} \ne f_{\rm M}$]] | [[File:P_ID1012__Mod_A_2_5_c.png|right|frame|Resulting baseband frequency response for $f_{\rm T} \ne f_{\rm M}$]] | ||
| − | *While the synchronous demodulator extracts information about the message signal from both sidebands in the same way at $f_{\rm T} = f_{\rm M} = 50 \ \rm kHz$ | + | *While the synchronous demodulator extracts information about the message signal from both sidebands in the same way at $f_{\rm T} = f_{\rm M} = 50 \ \rm kHz$, the lower sideband (LSB) provides the larger contribution at $f_{\rm T} = 55\ \rm kHz$. |
| Line 104: | Line 101: | ||
| − | '''(4)''' With the result of the previous subtask, one obtains: | + | '''(4)''' With the result of the previous subtask, one obtains: |
:$$ A_1 = 0.463 \cdot 2\,{\rm V}\hspace{0.15cm}\underline { = 0.926\,{\rm V}}\hspace{0.05cm},$$ | :$$ A_1 = 0.463 \cdot 2\,{\rm V}\hspace{0.15cm}\underline { = 0.926\,{\rm V}}\hspace{0.05cm},$$ | ||
:$$A_5 = 0.521 \cdot 3\,{\rm V} \hspace{0.15cm}\underline {= 1.563\,{\rm V}}\hspace{0.05cm}.$$ | :$$A_5 = 0.521 \cdot 3\,{\rm V} \hspace{0.15cm}\underline {= 1.563\,{\rm V}}\hspace{0.05cm}.$$ | ||
| − | *In | + | *In this case, the linear distortions are even less strong, since now also the $1 \ \rm kHz$ portion is attenuated more. |
| + | |||
'''(5)''' YES is correct: | '''(5)''' YES is correct: | ||
| − | *With the carrier frequency $f_{\rm T} = f_{\rm M} = 50 \ \rm kHz$ | + | *With the carrier frequency $f_{\rm T} = f_{\rm M} = 50 \ \rm kHz$, the $5 \ \rm kHz$ component is more attenuated than the $1 \ \rm kHz$ component, while at $f_{\rm T} = 55 \ {\rm kHz} \ne f_{\rm M}$, the $1 \ \rm kHz$ component is slightly more attenuated. |
| − | *If one | + | *If one chooses $f_{\rm T} \approx 54.5 \ \rm kHz$ for example, both components are attenuated equally $($by about the factor $0.53)$ and there is no or less distortion. |
| − | *However, this result is only valid for the source signal considered. Another $q(t)$ | + | *However, this result is only valid for the source signal considered. Another $q(t)$ with two spectral components would require a different "optimal carrier frequency". For a source signal with three or more spectral lines, linear distortions would always occur. |
| − | |||
{{ML-Fuß}} | {{ML-Fuß}} | ||
Latest revision as of 13:26, 6 December 2021
The communication system considered here is composed of the following blocks:
- DSB-AM without carrier $(f_{\rm T} = 50 \ \rm kHz$ or $f_{\rm T} = 55 \ \rm kHz)$:
- $$ s(t) = q(t) \cdot \cos (2 \pi f_{\rm T} \hspace{0.05cm} t).$$
- Gaussian band-pass channel; the magnitude $|f|$ in the exponent causes $H_K(–f) = H_K(f)$ to hold:
- $$H_{\rm K}(f) = {\rm e}^{-\pi \cdot \hspace{0.05cm} \left (({|f| - f_{\rm M}})/{\Delta f_{\rm K}}\right)^2} ,\hspace{0.2cm} f_{\rm M} = 50\,{\rm kHz},\hspace{0.2cm} \Delta f_{\rm K} = 10\,{\rm kHz}\hspace{0.05cm}.$$
- The synchronous demodulator has optimal parameters such that the sink signal $v(t)$ completely coincides with the source signal $q(t)$ when $H_{\rm K}(f) = 1$ ("ideal channel").
On the page Influence of linear channel distortions it was shown that the entire system is is sufficiently accurately characterized by the resulting frequency response
- $$H_{\rm MKD}(f) = {1}/{2} \cdot \big[ H_{\rm K}(f + f_{\rm T}) + H_{\rm K}(f - f_{\rm T})\big]$$
Here the subscript stands for $\rm M$odulator – $\rm K$ (for German "Kanal" i.e. channel) – $\rm D$emodulator.
The source signal $q(t)$ is composed of two cosine oscillations:
- $$q(t) = 2\,{\rm V}\cdot \cos (2 \pi \cdot 1\,{\rm kHz} \cdot t)+ 3\,{\rm V}\cdot \cos (2 \pi \cdot 5\,{\rm kHz} \cdot t)\hspace{0.05cm}.$$
Hints:
- This exercise belongs to the chapter Synchronous Demodulation.
- Particular reference is made to the page Influence of linear channel distortions.
Questions
Solution
(1) The equation given states that the band-pass frequency response $H_{\rm K}(f)$ has to be shifted to left and to right by the carrier frequency $f_{\rm T}$, and the two components have to be added up.
- The factor $1/2$ must still be taken into account (see plot).
- At low frequencies, this results in a Gaussian function around the center frequency "0":
- $$H_{\rm MKD}(f) = {\rm e}^{-\pi \cdot \hspace{0.05cm} \left ({f}/{\Delta f_{\rm K}}\right)^2} \hspace{0.05cm}.$$
- The two components at $±2f_{\rm T}$ need not be considered further. For the two frequencies we are looking for $f_1 = 1\ \rm kHz$ and $f_5 = 5 \ \rm kHz$, we obtain:
- $$ H_{\rm MKD}(f = f_1) = {\rm e}^{-\pi \cdot \hspace{0.05cm} \left (\frac{1\,{\rm kHz}}{10\,{\rm kHz}}\right)^2} = {\rm e}^{-\pi/100}\hspace{0.15cm}\underline {\approx 0.969} \hspace{0.05cm},$$
- $$H_{\rm MKD}(f = f_5) = {\rm e}^{-\pi \cdot \hspace{0.05cm} \left (\frac{5\,{\rm kHz}}{10\,{\rm kHz}}\right)^2} = {\rm e}^{-\pi/4} \hspace{0.3cm}\hspace{0.15cm}\underline {\approx 0.456} \hspace{0.05cm}.$$
(2) With $ω_1 = 2π · 1\ \rm kHz$ and $ω_5 = 2π · 5 \ \rm kHz$, it holds that:
- $$ v(t) = 0.969 \cdot 2\,{\rm V}\cdot \cos (\omega_1 \cdot t)+ 0.456 \cdot 3\,{\rm V}\cdot \cos (\omega_5 \cdot t) = \underline { 1.938\,{\rm V}}\cdot \cos (\omega_1 \cdot t) + \hspace{0.15cm}\underline {1.368\,{\rm V}}\cdot \cos (\omega_5 \cdot t) \hspace{0.05cm}.$$
- It can be seen that now – unlike the source signal $q(t)$ – the component at $1 \ \rm kHz$ ⇒ $A_1 = 1.938 \ \rm V$ is larger than the $5 \ \rm kHz$ component ⇒ $A_5 = 1.368 \ \rm V$, because the channel attenuates the $49 \ \rm kHz$ and $51 \ \rm kHz$ frequencies less than the spectral components at $45 \ \rm kHz$ and $55 \ \rm kHz$.
(3) The two spectral functions shifted by $±f_{\rm T}$ now no longer come to lie directly on top of each other, but there are an offset from each other by $10 \ \rm kHz$ .
- The resulting frequency response $H_{\rm MKD}(f)$ is thus no longer Gaussian, but characterized according to the sketch below:
- $$H_{\rm MKD}(f ) = {1}/{2}\cdot \left[{\rm e}^{-\pi \cdot \hspace{0.05cm} \left (\frac{f - 5\,{\rm kHz}}{10\,{\rm kHz}}\right)^2}+{\rm e}^{-\pi \cdot \hspace{0.05cm} \left (\frac{f + 5\,{\rm kHz}}{10\,{\rm kHz}}\right)^2}\right]\hspace{0.05cm}.$$
- For the frequencies $f_1$ and $f_5$ we get:
- $$H_{\rm MKD}(f = 1\,{\rm kHz}) = \frac{1}{2} \cdot \left[ H_{\rm K}(f = 56\,{\rm kHz}) + H_{\rm K}(f = -54\,{\rm kHz})\right]=$$
- $$\hspace{1.25cm}= \frac{1}{2}\cdot \left[{\rm e}^{-\pi \cdot \hspace{0.05cm} \left (\frac{56\, {\rm kHz}- 50\,{\rm kHz}}{10\,{\rm kHz}}\right)^2}+{\rm e}^{-\pi \cdot \hspace{0.05cm} \left (\frac{-54\, {\rm kHz}+ 50\,{\rm kHz}}{10\,{\rm kHz}}\right)^2}\right] = 0.161 + 0.302 \hspace{0.15cm}\underline {= 0.463}\hspace{0.05cm},$$
- $$H_{\rm MKD}(f = 5\,{\rm kHz}) = \frac{1}{2} \cdot \left[ H_{\rm K}(f = 60\,{\rm kHz}) + H_{\rm K}(f = -50\,{\rm kHz})\right]= \hspace{0.75cm}$$
- $$\hspace{1.25cm}= \frac{1}{2}\cdot \left[{\rm e}^{-\pi \cdot \hspace{0.05cm} \left (\frac{60\, {\rm kHz}- 50\,{\rm kHz}}{10\,{\rm kHz}}\right)^2}+{\rm e}^{-\pi \cdot \hspace{0.05cm} \left (\frac{-50\, {\rm kHz}+ 50\,{\rm kHz}}{10\,{\rm kHz}}\right)^2}\right] = 0.022 + 0.500 \hspace{0.15cm}\underline {= 0.521}\hspace{0.05cm}.$$
- While the synchronous demodulator extracts information about the message signal from both sidebands in the same way at $f_{\rm T} = f_{\rm M} = 50 \ \rm kHz$, the lower sideband (LSB) provides the larger contribution at $f_{\rm T} = 55\ \rm kHz$.
- For example, the LSB of the $5 \ \rm kHz$ component is now exactly at $f_{\rm M} = 50 \ \rm kHz$ and is transmitted undamped, while the USB is subject to heavy attenuation at $60 \ \rm kHz$ .
(4) With the result of the previous subtask, one obtains:
- $$ A_1 = 0.463 \cdot 2\,{\rm V}\hspace{0.15cm}\underline { = 0.926\,{\rm V}}\hspace{0.05cm},$$
- $$A_5 = 0.521 \cdot 3\,{\rm V} \hspace{0.15cm}\underline {= 1.563\,{\rm V}}\hspace{0.05cm}.$$
- In this case, the linear distortions are even less strong, since now also the $1 \ \rm kHz$ portion is attenuated more.
(5) YES is correct:
- With the carrier frequency $f_{\rm T} = f_{\rm M} = 50 \ \rm kHz$, the $5 \ \rm kHz$ component is more attenuated than the $1 \ \rm kHz$ component, while at $f_{\rm T} = 55 \ {\rm kHz} \ne f_{\rm M}$, the $1 \ \rm kHz$ component is slightly more attenuated.
- If one chooses $f_{\rm T} \approx 54.5 \ \rm kHz$ for example, both components are attenuated equally $($by about the factor $0.53)$ and there is no or less distortion.
- However, this result is only valid for the source signal considered. Another $q(t)$ with two spectral components would require a different "optimal carrier frequency". For a source signal with three or more spectral lines, linear distortions would always occur.